Lecture 1: Logic

From logic rules to programming constructs

1 In the Beginning there was Logos

What logical connectives do you know?

How can we define them? Think in terms of derivation trees:

\frac{\begin{matrix} \frac{\begin{matrix} \frac{\,}{\text{a premise}} & \frac{\,}{\text{another premise}} \end{matrix}}{\text{some fact}} & \frac{\frac{\,}{\text{this we have by default}}}{\text{another fact}} \end{matrix}}{\text{final conclusion}}

Define by providing rules for using the connectives: for example, a rule \frac{\begin{matrix} a & b \end{matrix}}{c} matches parts of the tree that have two premises, represented by variables a and b, and have any conclusion, represented by variable c.

Try to use only the connective you define in its definition.

2 Rules for Logical Connectives

Introduction rules say how to produce a connective.

Elimination rules say how to use it.

Text in parentheses is comments. Letters are variables: stand for anything.

Notations

{{{\frac{\,}{a} \tiny{x}} \atop {\text{\textbar}}} \atop {b}} \text{, \ \ or \ \ } {{{\frac{\,}{a} \tiny{x}} \atop {\text{\textbar}}} \atop {c}}

match any subtree that derives b (or c) and can use a (by assumption \frac{\,}{a} \tiny{x}) although otherwise a might not be warranted. For example:

\frac{\frac{\frac{\frac{\frac{\,}{\text{sunny}} \small{x}}{\text{go outdoor}}}{\text{playing}}}{\text{happy}}}{\text{sunny} \rightarrow \text{happy}} \small{\text{ using } x}

Such assumption can only be used in the matched subtree! But it can be used several times, e.g. if someone’s mood is more difficult to influence:

\frac{\frac{\begin{matrix} \frac{\frac{\frac{\,}{\text{sunny}} \small{x}}{\text{go outdoor}}}{\text{playing}} & \frac{\begin{matrix} \frac{\,}{\text{sunny}} \small{x} & \frac{\frac{\,}{\text{sunny}} \small{x}}{\text{go outdoor}} \end{matrix}}{\text{nice view}} \end{matrix}}{\text{happy}}}{\text{sunny} \rightarrow \text{happy}} \small{\text{ using } x}

Elimination rule for disjunction represents reasoning by cases.

How can we use the fact that it is sunny\veecloudy (but not rainy)?

\frac{\begin{matrix} \frac{\,}{\text{sunny} \vee \text{cloudy}} \tiny{\text{ forecast}} & \frac{\frac{\,}{\text{sunny}} \tiny{x}}{\text{no-umbrella}} & \frac{\frac{\,}{\text{cloudy}} \tiny{y}}{\text{no-umbrella}} \end{matrix}}{\text{no-umbrella}} \small{\text{ using } x, y}

We know that it will be sunny or cloudy, by watching weather forecast. If it will be sunny, we won’t need an umbrella. If it will be cloudy, we won’t need an umbrella. Therefore, won’t need an umbrella.We need one more kind of rules to do serious math: reasoning by induction (it is somewhat similar to reasoning by cases). Example rule for induction on natural numbers:

\frac{\begin{matrix} p (0) & {{{\frac{\,}{p(x)} \tiny{x}} \atop {\text{\textbar}}} \atop {p(x+1)}} \end{matrix}}{p (n)} \text{ by induction, using } x

So we get any p for any natural number n, provided we can get it for 0, and using it for x we can derive it for the successor x + 1, where x is a unique variable (we cannot substitute for it some particular number, because we write “using x” on the side).

3 Logos was Programmed in OCaml

3.1 Definitions

Writing out expressions and types repetitively is tedious: we need definitions. Definitions for types are written: type ty = some type.

• Writing A (s) : A ofa| B ofb in the table was cheating. Usually we have to define the type and then use it, e.g. using int for a and string for b:

  type int_string_choice = A of int | B of string

  allows us to write A (s) : int_string_choice.

• Without the type definition, it is difficult to know what other variants there are when one infers (i.e. “guesses”, computes) the type!

• In OCaml we can write `A(s) : [`A of a | `B of b]. With “`” variants, OCaml does guess what other variants are. These types are fun, but we will not use them in future lectures.

• Tuple elements don’t need labels because we always know at which position a tuple element stands. But having labels makes code more clear, so we can define a record type:

type int_string_record = {a: int; b: string}

and create its values: {a = 7; b = "Mary"}. * We access the fields of records using the dot notation:

{a=7; b="Mary"}.b = "Mary".Recursive expression {\texttt{rec}} \; x \; {\texttt{=}} \; e in the table was cheating: rec (usually called fix) cannot appear alone in OCaml! It must be part of a definition.

Definitions for expressions are introduced by rules a bit more complex than these:

\frac{\begin{matrix} e_{1} : a & {{{\frac{\,}{x : a} \tiny{x}} \atop {\text{\textbar}}} \atop {e_2 : b}} \end{matrix}}{{\texttt{let}} \; x \; {\texttt{=}} \; e_{1} \; {\texttt{in}} \; e_{2} : b}

(note that this rule is the same as introducing and eliminating \rightarrow), and:

\frac{\begin{matrix} {{{\frac{\,}{x : a} \tiny{x}} \atop {\text{\textbar}}} \atop {e_1 : a}} & {{{\frac{\,}{x : a} \tiny{x}} \atop {\text{\textbar}}} \atop {e_2 : b}} \end{matrix}}{{\texttt{let rec}} \; x \; {\texttt{=}} e_{1} \; {\texttt{in}} \; e_{2} \: b}

We will cover what is missing in above rules when we will talk about polymorphism.* Type definitions we have seen above are global: they need to be at the top-level, not nested in expressions, and they extend from the point they occur till the end of the source file or interactive session. * let-in definitions for expressions: {\texttt{let}} \; x \; {\texttt{=}} \; e_{1} \; {\texttt{in}} \; e_{2} are local, x is only visible in e_{2}. But let definitions are global: placing {\texttt{let}} \; x \; {\texttt{=}} \; e_{1} at the top-level makes x visible from after e_{1} till the end of the source file or interactive session. * In the interactive session, we mark an end of a top-level “sentence” by ;; – it is unnecessary in source files. * Operators like +, *, <, =, are names of functions. Just like other names, you can use operator names for your own functions:

let (+:) a b = String.concat “” [a; b];;Special way of defining”Alpha” +: “Beta”;;but normal way of using operators. * Operators in OCaml are not overloaded. It means, that every type needs its own set of operators. For example, +, , / work for intigers, while +., ., /. work for floating point numbers. Exception: comparisons <, =, etc. work for all values other than functions.

4 Exercises

Exercises from Think OCaml. How to Think Like a Computer Scientist by Nicholas Monje and Allen Downey.

1. Assume that we execute the following assignment statements:

   let width = 17;;let height = 12.0;;let delimiter = ‘.’;;

   For each of the following expressions, write the value of the expression and the type (of the value of the expression), or the resulting type error.

   1. width/2
   2. width/.2.0
   3. height/3
   4. 1 + 2 * 5
   5. delimiter * 5

2. Practice using the OCaml interpreter as a calculator:

   1. The volume of a sphere with radius r is \frac{4}{3} \pi r^3. What is the volume of a sphere with radius 5?

      Hint: 392.6 is wrong!

   2. Suppose the cover price of a book is $24.95, but bookstores get a 40% discount. Shipping costs $3 for the first copy and 75 cents for each additional copy. What is the total wholesale cost for 60 copies?

   3. If I leave my house at 6:52 am and run 1 mile at an easy pace (8:15 per mile), then 3 miles at tempo (7:12 per mile) and 1 mile at easy pace again, what time do I get home for breakfast?

3. You’ve probably heard of the fibonacci numbers before, but in case you haven’t, they’re defined by the following recursive relationship:

   \left\lbrace\begin{matrix} f (0) & = & 0 & \\\\\\ f (1) & = & 1 & \\\\\\ f (n + 1) & = & f (n) + f (n - 1) & \text{for } n = 2, 3, \ldots \end{matrix}\right.

   Write a recursive function to calculate these numbers.

4. A palindrome is a word that is spelled the same backward and forward, like “noon” and “redivider”. Recursively, a word is a palindrome if the first and last letters are the same and the middle is a palindrome.

   The following are functions that take a string argument and return the first, last, and middle letters:

   let firstchar word = word.[0];;let lastchar word = let len = String.length word - 1 in word.[len];;let middle word = let len = String.length word - 2 in String.sub word 1 len;;

   1. Enter these functions into the toplevel and test them out. What happens if you call middle with a string with two letters? One letter? What about the empty string, which is written ““?
   2. Write a function called is_palindrome that takes a string argument and returns true if it is a palindrome and false otherwise.

5. The greatest common divisor (GCD) of a and b is the largest number that divides both of them with no remainder.

   One way to find the GCD of two numbers is Euclid’s algorithm, which is based on the observation that if r is the remainder when a is divided by b, then \gcd (a, b) = \gcd (b, r). As a base case, we can consider \gcd (a, 0) = a.

   Write a function called gcd that takes parameters a and b and returns their greatest common divisor.

   If you need help, see http://en.wikipedia.org/wiki/Euclidean_algorithm.

Lecture 2: Algebra

Algebraic Data Types and some curious analogies

1 A Glimpse at Type Inference

For a refresher, let’s try to use the rules we introduced last time on some simple examples. Starting with fun x -> x. [?] will mean “dunno yet”.

\begin{matrix} & \frac{[?]}{{\texttt{fun x -> x}} : [?]} & \text{use } \rightarrow \text{ introduction:}\\\\\\ & \frac{\frac{\,}{{\texttt{x}} : a} \tiny{x}}{{\texttt{fun x -> x}} : [?] \rightarrow [?]} & \frac{\,}{{\texttt{x}} : a} \tiny{x} \text{ matches with } {{{\frac{\,}{x : a} \tiny{x}} \atop {\text{\textbar}}} \atop {e : b}} \text{ since } e = {\texttt{x}}\\\\\\ & \frac{\frac{\,}{{\texttt{x}} : a} \tiny{x}}{{\texttt{fun x -> x}} : a \rightarrow a} & \text{since } b = a \text{ because } x : a \text{ matched with } e : b \end{matrix}

Because a is arbitrary, OCaml puts a type variable 'a for it:

# fun x -> x;;
- : 'a -> 'a = <fun>

Let’s try fun x -> x+1, which is the same as fun x -> ((+) x) 1(try it with OCaml/F#!). [? \alpha] will mean “dunno yet, but the same as in other places with [? \alpha]”.

\begin{matrix} & \frac{[?]}{{\texttt{fun x -> ((+) x) 1}} : [?]} & \text{use } \rightarrow \text{ introduction:}\\\\\\ & \frac{\frac{[?]}{{\texttt{((+) x) 1}} : [? \alpha]}}{{\texttt{fun x -> ((+) x) 1}} : [?] \rightarrow [? \alpha]} & \text{use } \rightarrow \text{ elimination:}\\\\\\ & \frac{\frac{\begin{matrix} \frac{[?]}{{\texttt{(+) x}} : [? \beta] \rightarrow [? \alpha]} & \frac{[?]}{{\texttt{1}} : [? \beta]} \end{matrix}}{{\texttt{((+) x) 1}} : [? \alpha]}}{{\texttt{fun x -> ((+) x) 1}} : [?] \rightarrow [? \alpha]} & \text{we know that {\texttt{1}}} : {\texttt{int}}\\\\\\ & \frac{\frac{\begin{matrix} \frac{[?]}{{\texttt{(+) x}} : {\texttt{int}} \rightarrow [? \alpha]} & \frac{\,}{{\texttt{1}} : {\texttt{int}}} \tiny{\text{(constant)}} \end{matrix}}{{\texttt{((+) x) 1}} : [? \alpha]}}{{\texttt{fun x -> ((+) x) 1}} : [?] \rightarrow [? \alpha]} & \text{application again:}\\\\\\ & \frac{\frac{\begin{matrix} \frac{\begin{matrix} \frac{[?]}{{\texttt{(+)}} : [? \gamma] \rightarrow {\texttt{int}} \rightarrow [? \alpha]} & \frac{[?]}{{\texttt{x}} : [? \gamma]} \end{matrix}}{{\texttt{(+) x}} : {\texttt{int}} \rightarrow [? \alpha]} & \frac{\,}{{\texttt{1}} : {\texttt{int}}} \tiny{\text{(constant)}} \end{matrix}}{{\texttt{((+) x) 1}} : [? \alpha]}}{{\texttt{fun x -> ((+) x) 1}} : [?] \rightarrow [? \alpha]} & \text{it's our {\texttt{x}}!}\\\\\\ & \frac{\frac{\begin{matrix} \frac{\begin{matrix} \frac{[?]}{{\texttt{(+)}} : [? \gamma] \rightarrow {\texttt{int}} \rightarrow [? \alpha]} & \frac{\,}{{\texttt{x}} : [? \gamma]} \tiny{{\texttt{x}}} \end{matrix}}{{\texttt{(+) x}} : {\texttt{int}} \rightarrow [? \alpha]} & \frac{\,}{{\texttt{1}} : {\texttt{int}}} \tiny{\text{(constant)}} \end{matrix}}{{\texttt{((+) x) 1}} : [? \alpha]}}{{\texttt{fun x -> ((+) x) 1}} : [? \gamma] \rightarrow [? \alpha]} & \text{but {\texttt{(+)}}} : {\texttt{int}} \rightarrow {\texttt{int}} \rightarrow {\texttt{int}}\\\\\\ & \frac{\frac{\begin{matrix} \frac{\begin{matrix} \frac{\,}{{\texttt{(+)}} : {\texttt{int}} \rightarrow {\texttt{int}} \rightarrow {\texttt{int}}} \tiny{\text{(constant)}} & \frac{\,}{{\texttt{x}} : {\texttt{int}}} \tiny{{\texttt{x}}} \end{matrix}}{{\texttt{(+) x}} : {\texttt{int}} \rightarrow {\texttt{int}}} & \frac{\,}{{\texttt{1}} : {\texttt{int}}} \tiny{\text{(constant)}} \end{matrix}}{{\texttt{((+) x) 1}} : {\texttt{int}}}}{\text{{\texttt{fun x -> ((+) x) 1}}} : {\texttt{int}} \rightarrow {\texttt{int}}} & \end{matrix}

1.1 Curried form

When there are several arrows “on the same depth” in a function type, it means that the function returns a function: e.g. {\texttt{(+)}} : {\texttt{int}} \rightarrow {\texttt{int}} \rightarrow {\texttt{int}} is just a shorthand for {\texttt{(+)}} : {\texttt{int}} \rightarrow \left( {\texttt{int}} \rightarrow {\texttt{int}} \right). It is very different from

{\texttt{fun f -> (f 1) + 1}} : \left( {\texttt{int}} \rightarrow {\texttt{int}} \right) \rightarrow {\texttt{int}}

For addition, instead of (fun x -> x+1) we can write ((+) 1). What expanded form does ((+) 1) correspond to exactly (computationally)?

We will get used to functions returning functions when learning about the lambda calculus.

2 Algebraic Data Types

• Last time we learned about the unit type, variant types like:

type int_string_choice = A of int | B of string

and also tuple types, record types, and type definitions. * Variants don’t have to have arguments: instead of A of unit just use A. * In OCaml, variants take multiple arguments rather than taking tuples as arguments: A of int * string is different thanA of (int * string). But it’s not important unless you get bitten by it. * Type definitions can be recursive!

type int_list = Empty | Cons of int * int_list

Let’s see what we have in int_list:Empty, Cons (5, Cons (7, Cons (13, Empty))), etc. * Type bool can be seen as type bool = true | false, type int can be seen as a very large type int = 0 | -1 | 1 | -2 | 2 | … * Type definitions can be parametric with respect to types of their components (more on this in lecture about polymorphism), for example a list elements of arbitrary type:

type 'elem list = Empty | Cons of 'elem * 'elem list

• Type variables must start with ’, but since OCaml will not remember the names we give, it’s customary to use the names OCaml uses: 'a, 'b, 'c, 'd…
• The syntax in OCaml is a bit strange: in F# we write list<'elem>. OCaml syntax mimics English, silly example:

  type 'white_color dog = Dog of 'white_color

• With multiple parameters:
  • OCaml:type ('a, 'b) choice = Left of 'a | Right of 'b
  • F#:type choice<'a,'b> = Left of 'a | Right of 'b
  • Haskell:data Choice a b = Left a | Right b

3 Syntactic Bread and Sugar

• Names of variants, called constructors, must start with capital letter – so if we wanted to define our own booleans, it would be

type my_bool = True | False

Only constructors and module names can start with capital letter. * Modules are “shelves” with values. For example, List has operations on lists, like List.map and List.filter. * Did I mention that we can use record.field to access a field? * fun x y -> e stands for fun x -> fun y -> e, etc. – and of course,fun x -> fun y -> e parses as fun x -> (fun y -> e) * function A x -> e1 | B y -> e2 stands for fun p -> match p with A x -> e1 | B y -> e2, etc. * the general form is: function *PATTERN-MATCHING* stands forfun v -> match v with *PATTERN-MATCHING* * let f ARGS = e is a shorthand for let f = fun ARGS -> e

4 Pattern Matching

• Recall that we introduced fst and snd as means to access elements of a pair. But what about bigger tuples? The “basic” way of accessing any tuple reuses the match construct. Functions fst and snd can easily be defined!

let fst = fun p -> match p with (a, b) -> a
let snd = fun p -> match p with (a, b) -> b

• It also works with records:

type person = {name: string; surname: string; age: int}
match {name="Walker"; surname="Johnnie"; age=207}
with {name=n; surname=sn; age=a} -> "Hi "^sn^"!"

• The left-hand-sides of -> in match expressions are called patterns.
• Patterns can be nested:

match Some (5, 7) with None -> "sum: nothing"
  | Some (x, y) -> "sum: " ^ string_of_int (x+y)

• A pattern can just match the whole value, without performing destructuring: match f x with v ->… is the same as let v = f x in …
• When we do not need a value in a pattern, it is good practice to use the underscore: _ (which is not a variable!)

let fst (a,_) = a
let snd (_,b) = b

• A variable can only appear once in a pattern (it is called linearity).
• But we can add conditions to the patterns after when, so linearity is not really a problem!

match p with (x, y) when x = y -> "diag" | _ -> "off-diag"

let compare a b = match a, b with
  | (x, y) when x < y -> -1
  | (x, y) when x = y -> 0
  | _ -> 1

• We can skip over unused fields of a record in a pattern.
• We can compress our patterns by using | inside a single pattern:

type month =
  | Jan | Feb | Mar | Apr | May | Jun
  | Jul | Aug | Sep | Oct | Nov | Dec
type weekday = Mon | Tue | Wed | Thu | Fri | Sat | Sun
type date =
  {year: int; month: month; day: int; weekday: weekday}
let day =
  {year = 2012; month = Feb; day = 14; weekday = Wed};;
match day with
  | {weekday = Sat | Sun} -> "Weekend!"
  | _ -> "Work day"

• We use (pattern **as** v) to name a nested pattern:

match day with
  | {weekday = (Mon | Tue | Wed | Thu | Fri **as** wday)}
      when not (day.month = Dec && day.day = 24) ->
    Some (work (get_plan wday))
  | _ -> None

5 Interpreting Algebraic DTs as Polynomials

Let’s do a peculiar translation: take a data type and replace | with +, * with \times, treating record types as tuple types (i.e. erasing field names and translationg ; as \times).

There is a special type for which we cannot build a value:

type void

(yes, it is its definition, no = something part). Translate it as 0.

Translate the unit type as 1. Since variants without arguments behave as variants of unit, translate them as 1 as well. Translate bool as 2.

Translate int, string, float, type parameters and other types of interest as variables. Translate defined types by their translations (substituting variables if necessary).

Give name to the type being defined (denoting a function of the variables introduced). Now interpret the result as ordinary numeric polynomial! (Or “rational function” if it is recursively defined.)

Let’s have fun with it.

type date = {year: int; month: int; day: int}

D = xxx = x^3

type 'a option = None | Some of 'a   (* built-in type *)

O = 1 + x

type 'a my_list = Empty | Cons of 'a * 'a my_list

L = 1 + xL

type btree = Tip | Node of int * btree * btree

T = 1 + xTT = 1 + xT^2

When translations of two types are equal according to laws of high-school algebra, the types are isomorphic, that is, there exist 1-to-1 functions from one type to the other.

Let’s play with the type of binary trees:

\begin{matrix} T & = & 1 + xT^2 = 1 + xT + x^2 T^3 = 1 + x + x^2 T^2 + x^2 T^3 =\\\\\\ & = & 1 + x + x^2 T^2 (1 + T) = 1 + x (1 + xT^2 (1 + T)) \end{matrix}

Now let’s translate the resulting type:

type repr =
  (int * (int * btree * btree * btree option) option) option

Try to find the isomorphism functions iso1 and iso2

val iso1 : btree -> repr
val iso2 : repr -> btree

i.e. functions such that for all trees t, iso2 (iso1 t) = t, and for all representations r, iso1 (iso2 r) = r.

My first failed attempt:

# let iso1 (t : btree) : repr =
  match t with
    | Tip -> None
    | Node (x, Tip, Tip) -> Some (x, None)
    | Node (x, Node (y, t1, t2), Tip) ->
      Some (x, Some (y, t1, t2, None))
    | Node (x, Node (y, t1, t2), t3) ->
      Some (x, Some (y, t1, t2, Some t3));;
            Characters 32-261: […]
Warning 8: this pattern-matching is not exhaustive.
Here is an example of a value that is not matched:
Node (_, Tip, Node (_, _, _))

I forgot about one case. It seems difficult to guess the solution, have you found it on your try?

Let’s divide the task into smaller steps corresponding to selected intermediate points in the transformation of the polynomial:

type ('a, 'b) choice = Left of 'a | Right of 'b
type interm1 =
  ((int * btree, int * int * btree * btree * btree) choice)
  option
type interm2 =
  ((int, int * int * btree * btree * btree option) choice)
  option

let step1r (t : btree) : interm1 =
  match t with
    | Tip -> None
    | Node (x, t1, Tip) -> Some (Left (x, t1))
    | Node (x, t1, Node (y, t2, t3)) ->
      Some (Right (x, y, t1, t2, t3))

let step2r (r : interm1) : interm2 =
  match r with
    | None -> None
    | Some (Left (x, Tip)) -> Some (Left x)
    | Some (Left (x, Node (y, t1, t2))) ->
      Some (Right (x, y, t1, t2, None))
    | Some (Right (x, y, t1, t2, t3)) ->
      Some (Right (x, y, t1, t2, Some t3))

let step3r (r : interm2) : repr =
  match r with
    | None -> None
    | Some (Left x) -> Some (x, None)
    | Some (Right (x, y, t1, t2, t3opt)) ->
      Some (x, Some (y, t1, t2, t3opt))

let iso1 (t : btree) : repr =
  step3r (step2r (step1r t))

Define step1l, step2l, step3l, and iso2. Hint: now it’s trivial!

Take-home lessons:

• Try to define data structures so that only information that makes sense can be represented – as long as it does not overcomplicate the data structures. Avoid catch-all clauses when defining functions. The compiler will then tell you if you have forgotten about a case.
• Divide solutions into small steps so that each step can be easily understood and checked.

5.1 Differentiating Algebraic Data Types

Of course, you would say, the pompous title is wrong, we will differentiate the translated polynomials. But what sense does it make?

It turns out, that taking the partial derivative of a polynomial resulting from translating a data type, gives us, when translated back, a type representing how to change one occurrence of a value of type corresponding to the variable with respect to which we computed the partial derivative.

Take the “date” example:

type date = {year: int; month: int; day: int}

\begin{matrix} D & = & xxx = x^3\\\\\\ \frac{\partial D}{\partial x} & = & 3 x^2 = xx + xx + xx \end{matrix}

(we could have left it at 3 xx as well). Now we construct the type:

type date_deriv =
  Year of int * int | Month of int * int | Day of int * int

Now we need to introduce and use (“eliminate”) the type date_deriv.

let date_deriv {year=y; month=m; day=d} =
  [Year (m, d); Month (y, d); Day (y, m)]

let date_integr n = function
  | Year (m, d) -> {year=n; month=m; day=d}
  | Month (y, d) -> {year=y; month=n; day=d}
  | Day (y, m) -> {year=y; month=m, day=n}
;;
List.map (date_integr 7)
  (date_deriv {year=2012; month=2; day=14})

Let’s do now the more difficult case of binary trees:

type btree = Tip | Node of int * btree * btree

\begin{matrix} T & = & 1 + xT^2\\\\\\ \frac{\partial T}{\partial x} & = & 0 + T^2 + 2 xT \frac{\partial T}{\partial x} = TT + 2 xT \frac{\partial T}{\partial x} \end{matrix}

(again, we could expand further into \frac{\partial T}{\partial x} = TT + xT \frac{\partial T}{\partial x} + xT \frac{\partial T}{\partial x}).

Instead of translating 2 as bool, we will introduce new type for clarity:

type btree_dir = LeftBranch | RightBranch
type btree_deriv =
  | Here of btree * btree
  | Below of btree_dir * int * btree * btree_deriv

(You might someday hear about zippers – they are “inverted” w.r.t. our type, in zippers the hole comes first.)

Write a function that takes a number and a btree_deriv, and builds a btree by putting the number into the “hole” in btree_deriv.

Solution:

let rec btree_integr n =
  | Here (ltree, rtree) -> Node (n, ltree, rtree)
  | Below (LeftBranch, m, rtree) ->
    Node (m, btree_integr n ltree, rtree)
  | Below (RightBranch, m, ltree) ->
    Node (m, ltree, btree_integr n rtree)

6 Homework

Write a function btree_deriv_at that takes a predicate over integers (i.e. a function f: int -> bool), and a btree, and builds a btree_deriv whose “hole” is in the first position for which the predicate returns true. It should actually return a btree_deriv option, with None in case the predicate does not hold for any node.

This homework is due for the class after the Computation class, i.e. for (before) the Functions class.

Chapter 2: Derivation example

Lecture 2: Algebra

Type inference example derivation

\frac{[?]}{{\texttt{fun x -> ((+) x) 1}} : [?]}

\text{use } \rightarrow \text{ introduction:}

\frac{\frac{[?]}{{\texttt{((+) x) 1}} : [? \alpha]}}{{\texttt{fun x -> ((+) x) 1}} : [?] \rightarrow [? \alpha]}

\text{use } \rightarrow \text{ elimination:}

\frac{\frac{\begin{matrix} \frac{[?]}{{\texttt{(+) x}} : [? \beta] \rightarrow [? \alpha]} & \frac{[?]}{{\texttt{1}} : [? \beta]} \end{matrix}}{{\texttt{((+) x) 1}} : [? \alpha]}}{{\texttt{fun x -> ((+) x) 1}} : [?] \rightarrow [? \alpha]}

\text{we know that {\texttt{1}}} : {\texttt{int}}

\frac{\frac{\begin{matrix} \frac{[?]}{{\texttt{(+) x}} : {\texttt{int}} \rightarrow [? \alpha]} & \frac{\,}{{\texttt{1}} : {\texttt{int}}} \tiny{\text{(constant)}} \end{matrix}}{{\texttt{((+) x) 1}} : [? \alpha]}}{{\texttt{fun x -> ((+) x) 1}} : [?] \rightarrow [? \alpha]}

\text{application again:}

\frac{\frac{\begin{matrix} \frac{\begin{matrix} \frac{[?]}{{\texttt{(+)}} : [? \gamma] \rightarrow {\texttt{int}} \rightarrow [? \alpha]} & \frac{[?]}{{\texttt{x}} : [? \gamma]} \end{matrix}}{{\texttt{(+) x}} : {\texttt{int}} \rightarrow [? \alpha]} & \frac{\,}{{\texttt{1}} : {\texttt{int}}} \tiny{\text{(constant)}} \end{matrix}}{{\texttt{((+) x) 1}} : [? \alpha]}}{{\texttt{fun x -> ((+) x) 1}} : [?] \rightarrow [? \alpha]}

\text{it's our {\texttt{x}}!}

\frac{\frac{\begin{matrix} \frac{\begin{matrix} \frac{[?]}{{\texttt{(+)}} : [? \gamma] \rightarrow {\texttt{int}} \rightarrow [? \alpha]} & \frac{\,}{{\texttt{x}} : [? \gamma]} {\texttt{x}} \end{matrix}}{{\texttt{(+) x}} : {\texttt{int}} \rightarrow [? \alpha]} & \frac{\,}{{\texttt{1}} : {\texttt{int}}} \tiny{\text{(constant)}} \end{matrix}}{{\texttt{((+) x) 1}} : [? \alpha]}}{{\texttt{fun x -> ((+) x) 1}} : [? \gamma] \rightarrow [? \alpha]}

\text{but {\texttt{(+)}}} : {\texttt{int}} \rightarrow {\texttt{int}} \rightarrow {\texttt{int}}

\frac{\frac{\begin{matrix} \frac{\begin{matrix} \frac{\,}{{\texttt{(+)}} : {\texttt{int}} \rightarrow {\texttt{int}} \rightarrow {\texttt{int}}} \tiny{\text{(constant)}} & \frac{\,}{{\texttt{x}} : {\texttt{int}}} {\texttt{x}} \end{matrix}}{{\texttt{(+) x}} : {\texttt{int}} \rightarrow {\texttt{int}}} & \frac{\,}{{\texttt{1}} : {\texttt{int}}} \tiny{\text{(constant)}} \end{matrix}}{{\texttt{((+) x) 1}} : {\texttt{int}}}}{\text{{\texttt{fun x -> ((+) x) 1}}} : {\texttt{int}} \rightarrow {\texttt{int}}}

Exercise 1.

Due to Yaron Minsky.

Consider a datatype to store internet connection information. The time when_initiated marks the start of connecting and is not needed after the connection is established (it is only used to decide whether to give up trying to connect). The ping information is available for established connection but not straight away.

type connectionstate = | Connecting | Connected | Disconnectedtype connectioninfo = { state : connectionstate; server : Inetaddr.t;
lastpingtime : Time.t option; lastpingid : int option; sessionid : string option; wheninitiated : Time.t option; whendisconnected : Time.t option;}

(The types Time.t and Inetaddr.t come from the library Core used where Yaron Minsky works. You can replace them with float and Unix.inet_addr. Load the Unix library in the interactive toplevel by #load "unix.cma";;.) Rewrite the type definitions so that the datatype will contain only reasonable combinations of information.

Exercise 2.

In OCaml, functions can have named arguments, and also default arguments (parameters, possibly with default values, which can be omitted when providing arguments). The names of arguments are called labels. The labels can be different from the names of the argument values:

let f \simmeaningfulname:n = n+1let = f \simmeaningfulname:5We do not need the result so we ignore it.

When the label and value names are the same, the syntax is shorter:

let g \simpos \simlen = StringLabels.sub “0123456789abcdefghijklmnopqrstuvwxyz” \simpos \simlenlet () =A nicer way to mark computations that do not produce a result (return unit). let pos = Random.int 26 in let len = Random.int 10 in printstring (g \simpos \simlen)

When some function arguments are optional, the function has to take non-optional arguments after the last optional argument. When the optional parameters have default values:

let h ?(len=1) pos = g \simpos \simlenlet () = printstring (h 10)

Optional arguments are implemented as parameters of an option type. This allows us to check whether the argument was actually provided:

let foo ?bar n = match bar with | None -> “Argument =” stringofint n | Some m -> “Sum =” stringofint (m + n);;foo 5;;foo \simbar:5 7;;

We can also provide the option value directly:

let bar = if Random.int 10 < 5 then None else Some 7 infoo ?bar 7;;

1. Observe the types that functions with labelled and optional arguments have. Come up with coding style guidelines, e.g. when to use labeled arguments.
2. Write a rectangle-drawing procedure that takes three optional arguments: left-upper corner, right-lower corner, and a width-height pair. It should draw a correct rectangle whenever two arguments are given, and raise exception otherwise. Load the graphics library in the interactive toplevel by #load "graphics.cma";;. Use “functions” invalid_arg, Graphics.open_graph and Graphics.draw_rect.
3. Write a function that takes an optional argument of arbitrary type and a function argument, and passes the optional argument to the function without inspecting it.

Exercise 3.

From last year’s exam.

1. Give the (most general) types of the following expressions, either by guessing or inferring by hand:
   1. let double f y = f (f y) in fun g x -> double (g x)
   2. let rec tails l = match l with [] -> [] | x::xs -> xs::tails xs infun l -> List.combine l (tails l)
2. Give example expressions that have the following types (without using type constraints):
   1. (int -> int) -> bool
   2. 'a option -> 'a list

Exercise 4.

We have seen in the class, that algebraic data types can be related to analytic functions (the subset that can be defined out of polynomials via recursion) – by literally interpreting sum types (i.e. variant types) as sums and product types (i.e. tuple and record types) as products. We can extend this interpretation to all OCaml types that we introduced, by interpreting a function type a \rightarrow b as b^a, b to the power of a. Note that the b^a notation is actually used to denote functions in set theory.

1. Translate a^{b + cd} and a^b (a^c)^d into OCaml types, using any distinct types for a, b, c, d, and using the ('a,'b) choice = Left of 'a | Right of 'b datatype for +. Write the bijection function in both directions.
2. Come up with a type 't exp, that shares with the exponential function the following property: \frac{\partial \exp (t)}{\partial t} = \exp (t), where we translate a derivative of a type as a context, i.e. the type with a “hole”, as in the lecture. Explain why your answer is correct. Hint: in computer science, our logarithms are mostly base 2.

Further reading: http://bababadalgharaghtakamminarronnkonnbro.blogspot.com/2012/10/algebraic-type-systems-combinatorial.html

Lecture 3: Computation

‘‘Using, Understanding and Unraveling the OCaml Language’’ Didier Rémy, chapter 1

‘‘The OCaml system’’ manual, the tutorial part, chapter 1

1 Function Composition

• The usual way function composition is defined in math is “backward”:
  • math: (f \circ g) (x) = f (g (x))
  • OCaml: let (-|) f g x = f (g x)
  • F#: let (<<) f g x = f (g x)
  • Haskell: (.) f g = \x -> f (g x)
• It looks like function application, but needs less parentheses. Do you recall the functions iso1 and iso2 from previous lecture?

let iso2 = step1l -| step2l -| step3l

• A more natural definition of function composition is “forward”:
  • OCaml: let (|-) f g x = g (f x)
  • F#: let (>>) f g x = g (f x)
• It follows the order in which computation proceeds.

let iso1 = step1r |- step2r |- step3r

• Partial application is e.g. ((+) 1) from last week: we don’t pass all arguments a function needs, in result we get a function that requires the remaining arguments. How is it used above?
• Now we define f^n (x) := (f \circ \ldots \circ f) (x) (f appears n times).

let rec power f n =
  if n <= 0 then (fun x -> x) else f -| power f (n-1)

• Now we define a numerical derivative:

let derivative dx f = fun x -> (f(x +. dx) -. f(x)) /. dx

where the intent to use with two arguments is stressed, or for short:

let derivative dx f x = (f(x +. dx) -. f(x)) /. dx

• We have (+): int -> int -> int, so cannot use with floating point numbers – operators followed by dot work on float numbers.

let pi = 4.0 *. atan 1.0
let sin''' = (power (derivative 1e-5) 3) sin;;
sin''' pi;;

2 Evaluation Rules (reduction semantics)

• Programs consist of expressions:

  \begin{matrix} a := & x & \text{variables}\\\\\\ | & {\texttt{fun }} x {\texttt{->}} a & \text{(defined) functions}\\\\\\ | & a a & \text{applications}\\\\\\ | & C^0 & \text{value constructors of arity } 0\\\\\\ | & C^n (a, \ldots, a) & \text{value constructors of arity } n \\\\\\ | & f^n & \text{built-in values (primitives) of a. } n\\\\\\ | & {\texttt{let }} x = a {\texttt{ in }} a & \text{name bindings (local definitions)}\\\\\\ | & {\texttt{match }} a {\texttt{ with} \ \ \ \ \ \ \ } & \\\\\\ & p {\texttt{->}} a \text{{\texttt{ \textbar }}} \ldots {\texttt{ \textbar }} p {\texttt{->}} a & \text{pattern matching}\\\\\\ p := & x & \text{pattern variables}\\\\\\ | & (p, \ldots, p) & \text{tuple patterns}\\\\\\ | & C^0 & \text{variant patterns of arity } 0\\\\\\ | & C^n (p, \ldots, p) & \text{variant patterns of arity } n \end{matrix}

• Arity means how many arguments something requires; (and for tuples, the length of a tuple).

• To simplify presentation, we will use a primitive fix to define a limited form of let rec:

  {\texttt{let rec }} f {\texttt{ }} x = e_{1} {\texttt{ in }} e_{2} \equiv {\texttt{let }} f = {\texttt{fix (fun }} f {\texttt{ }} x {\texttt{->}} e_{1} {\texttt{) in }} e_{2}

• Expressions evaluate (i.e. compute) to values:

  \begin{matrix} v := & {\texttt{fun }} x {\texttt{->}} a & \text{(defined) functions}\\\\\\ | & C^n (v_{1}, \ldots, v_{n}) & \text{constructed values}\\\\\\ | & f^n v_{1} \ldots v_{k} & k < n \text{ partially applied primitives} \end{matrix}

• To substitute a value v for a variable x in expression a we write a [x := v] – it behaves as if every occurrence of x in a was rewritten by v.

  • (But actually the value v is not duplicated.)

• Reduction (i.e. computation) proceeds as follows: first we give redexes

  \begin{matrix} \left( {\texttt{fun }} x {\texttt{->}} a \right) v & \rightsquigarrow & a [x := v]\\\\\\ {\texttt{let }} x = v {\texttt{ in }} a & \rightsquigarrow & a [x := v]\\\\\\ f^n v_{1} \ldots v_{n} & \rightsquigarrow & f (v_{1}, \ldots, v_{n})\\\\\\ {\texttt{match }} v {\texttt{ with} } x {\texttt{->}} a {\texttt{ \textbar }} \ldots & \rightsquigarrow & a [x := v]\\\\\\ {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n}) {\texttt{ with}} & & \\\\\\ C_{2}^n (p_{1}, \ldots, p_{k}) {\texttt{->}} a {\texttt{ \textbar }} \operatorname{pm} & \rightsquigarrow & {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n})\\\\\\ & & {\texttt{with} } \operatorname{pm}\\\\\\ {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n}) {\texttt{ with}} & & \\\\\\ C_{1}^n (x_{1}, \ldots, x_{n}) {\texttt{->}} a {\texttt{ \textbar }} \ldots & \rightsquigarrow & a [x_{1} \:= v_{1} ; \ldots ; x_{n} := v_{n}] \end{matrix}

  If n = 0, C_{1}^n (v_{1}, \ldots, v_{n}) stands for C^0_{1}, etc. By f (v_{1}, \ldots, v_{n}) we denote the actual value resulting from computing the primitive. We omit the more complex cases of pattern matching.

• Rule variables: x matches any expression/pattern variable; a, a_{1}, \ldots, a_{n} match any expression; v, v_{1}, \ldots, v_{n} match any value. Substitute them so that the left-hand-side of a rule is your expression, then the right-hand-side is the reduced expression.

• The remaining rules evaluate the arguments in arbitrary order, but keep the order in which let…in and match…with is evaluated.

  If a_{i} \rightsquigarrow a_{i}', then:

  \begin{matrix} a_{1} a_{2} & \rightsquigarrow & a_{1}' a_{2}\\\\\\ a_{1} a_{2} & \rightsquigarrow & a_{1} a_{2}'\\\\\\ C^n (a_{1}, \ldots, a_{i}, \ldots, a_{n}) & \rightsquigarrow & C^n (a_{1}, \ldots, a_{i}', \ldots, a_{n})\\\\\\ {\texttt{let }} x = a_{1} {\texttt{ in }} a_{2} & \rightsquigarrow & {\texttt{let }} x = a_{1}' {\texttt{ in }} a_{2}\\\\\\ {\texttt{match }} a_{1} {\texttt{ with} } \operatorname{pm} & \rightsquigarrow & {\texttt{match }} a_{1}' {\texttt{ with} } \operatorname{pm} \end{matrix}

• Finally, we give the rule for the primitive fix – it is a binary primitive:

  \begin{matrix} {\texttt{fix}}^2 v_{1} v_{2} & \rightsquigarrow & v_{1} \left( {\texttt{fix}}^2 v_{1} \right) v_{2} \end{matrix}

  Because fix is binary, \left( {\texttt{fix}}^2 v_{1} \right) is already a value so it will not be further computed until it is applied inside of v_{1}.

• Compute some programs using the rules by hand.

3 Symbolic Derivation Example

Go through the examples from the Lec3.ml file in the toplevel.

eval_1_2 <-- 3.00 * x + 2.00 * y + x * x * y
  eval_1_2 <-- x * x * y
    eval_1_2 <-- y
    eval_1_2 --> 2.
    eval_1_2 <-- x * x
      eval_1_2 <-- x
      eval_1_2 --> 1.
      eval_1_2 <-- x
      eval_1_2 --> 1.
    eval_1_2 --> 1.
  eval_1_2 --> 2.
  eval_1_2 <-- 3.00 * x + 2.00 * y
    eval_1_2 <-- 2.00 * y
      eval_1_2 <-- y
      eval_1_2 --> 2.
      eval_1_2 <-- 2.00
      eval_1_2 --> 2.
    eval_1_2 --> 4.
    eval_1_2 <-- 3.00 * x
      eval_1_2 <-- x
      eval_1_2 --> 1.
      eval_1_2 <-- 3.00
      eval_1_2 --> 3.
    eval_1_2 --> 3.
  eval_1_2 --> 7.
eval_1_2 --> 9.
- : float = 9.

4 Tail Calls (and tail recursion)

• Excuse me for not defining what a function call is…
• Computers normally evaluate programs by creating stack frames on the stack for function calls (roughly like indentation levels in the above example).
• A tail call is a function call that is performed last when computing a function.
• Functional language compilers will often insert a “jump” for a tail call instead of creating a stack frame.
• A function is tail recursive if it calls itself, and functions it mutually-recursively depends on, only using a tail call.
• Tail recursive functions often have special accumulator arguments that store intermediate computation results which in a non-tail-recursive function would just be values of subexpressions.
• The accumulated result is computed in “reverse order” – while climbing up the recursion rather than while descending (i.e. returning) from it.
• The issue is more complex for lazy programming languages like Haskell.
• Compare:

# let rec unfold n = if n <= 0 then [] else n :: unfold (n-1);;
val unfold : int -> int list = <fun>
# unfold 100000;;
- : int list =
[100000; 99999; 99998; 99997; 99996; 99995; 99994; 99993; …]
# unfold 1000000;;
Stack overflow during evaluation (looping recursion?).
# let rec unfold_tcall acc n =
  if n <= 0 then acc else unfold_tcall (n::acc) (n-1);;
  val unfold_tcall : int list -> int -> int list = <fun>
# unfold_tcall [] 100000;;
- : int list =
[1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; …]
# unfold_tcall [] 1000000;;
- : int list =
[1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; …]

• Is it possible to find the depth of a tree using a tail-recursive function?

5 First Encounter of Continuation Passing Style

We can postpone doing the actual work till the last moment:

let rec depth tree k = match tree with
    | Tip -> k 0
    | Node(_,left,right) ->
      depth left (fun dleft ->
        depth right (fun dright ->
          k (1 + (max dleft dright))))

let depth tree = depth tree (fun d -> d)

6 Homework

By “traverse a tree” below we mean: write a function that takes a tree and returns a list of values in the nodes of the tree.

1. Write a function (of type btree -> int list) that traverses a binary tree: in prefix order – first the value stored in a node, then values in all nodes to the left, then values in all nodes to the right;
2. in infix order – first values in all nodes to the left, then value stored in a node, then values in all nodes to the right (so it is “left-to-right” order);
3. in breadth-first order – first values in more shallow nodes.
4. Turn the function from ex. 1 or 2 into continuation passing style.
5. Do the homework from the end of last week slides: write btree_deriv_at.
6. Write a function simplify: expression -> expression that simplifies the expression a bit, so that for example the result of simplify (deriv exp dv) looks more like what a human would get computing the derivative of exp with respect to dv.
   • Write a simplify_once function that performs a single step of the simplification, and wrap it using a general fixpoint function that performs an operation until a fixed point is reached: given f and x, it computes f^n (x) such that f^n (x) = f^{n + 1} (x).

Functional Programming

Computation

Exercise 1: By “traverse a tree” below we mean: write a function that takes a tree and returns a list of values in the nodes of the tree.

1. Write a function (of type *btree -> int list*) that traverses a binary tree: in prefix order – first the value stored in a node, then values in all nodes to the left, then values in all nodes to the right;
2. in infix order – first values in all nodes to the left, then value stored in a node, then values in all nodes to the right (so it is “left-to-right” order);
3. in breadth-first order – first values in more shallow nodes.

Exercise 2: Turn the function from ex. 1 point 1 or 2 into continuation passing style.

Exercise 3: Do the homework from the end of last week slides: write btree_deriv_at.

Exercise 4: Write a function simplify: expression -> expression that simplifies the expression a bit, so that for example the result of simplify (deriv exp dv) looks more like what a human would get computing the derivative of exp with respect to dv:

Write a simplify_once function that performs a single step of the simplification, and wrap it using a general fixpoint function that performs an operation until a fixed point* is reached: given f and x, it computes f^n (x) such that f^n (x) = f^{n + 1} (x).*

Exercise 5: Write two sorting algorithms, working on lists: merge sort and quicksort.

1. Merge sort splits the list roughly in half, sorts the parts, and merges the sorted parts into the sorted result.
2. Quicksort splits the list into elements smaller/greater than the first element, sorts the parts, and puts them together.

Lecture 4: Functions.

Programming in untyped \lambda-calculus.

Introduction to Lambda Calculus Henk Barendregt, Erik Barendsen

Lecture Notes on the Lambda Calculus Peter Selinger

1 Review: a “computation by hand” example

Let’s compute some larger, recursive program.Recall that we use fix instead of let rec to simplify rules for recursion. Also remember our syntactic conventions: fun x y -> e stands for fun x -> (fun y -> e), etc.

let rec fix f x = f (fix f) xPreparations.type intlist = Nil | Cons of int * intlistWe will evaluate (reduce) the following expression.let length = fix (fun f l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + f xs) inlength (Cons (1, (Cons (2, Nil))))

let length = fix (fun f l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + f xs) inlength (Cons (1, (Cons (2, Nil))))

\begin{matrix} {\texttt{let }} x = v {\texttt{ in }} a & \Downarrow & a [x := v] \end{matrix}

fix (fun f l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + f xs) (Cons (1, (Cons (2, Nil))))

\begin{matrix} {\texttt{fix}}^2 v_{1} v_{2} & \Downarrow & v_{1} \left( {\texttt{fix}}^2 v_{1} \right) v_{2} \end{matrix}

\begin{matrix} {\texttt{fix}}^2 v_{1} v_{2} & \Downarrow & v_{1} \left( {\texttt{fix}}^2 v_{1} \right) v_{2} \end{matrix}

(fun f l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + f xs) (fix (fun f l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + f xs)) (Cons (1, (Cons (2, Nil))))

\begin{matrix} \left( {\texttt{fun }} x {\texttt{->}} a \right) v & \rightsquigarrow & a [x := v]\\\\\\ a_{1} a_{2} & \Downarrow & a_{1}' a_{2} \end{matrix}

\begin{matrix} \left( {\texttt{fun }} x {\texttt{->}} a \right) v & \rightsquigarrow & a [x := v]\\\\\\ a_{1} a_{2} & \Downarrow & a_{1}' a_{2} \end{matrix}

(fun l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + (fix (fun f l -> match l with | Nil -> 0
| Cons (x, xs) -> 1 + f xs)) xs) (Cons (1, (Cons (2, Nil))))

\begin{matrix} \left( {\texttt{fun }} x {\texttt{->}} a \right) v & \Downarrow & a [x := v] \end{matrix}

\begin{matrix} \left( {\texttt{fun }} x {\texttt{->}} a \right) v & \Downarrow & a [x := v] \end{matrix}

(match Cons (1, (Cons (2, Nil))) with | Nil -> 0 | Cons (x, xs) -> 1 + (fix (fun f l -> match l with | Nil -> 0
| Cons (x, xs) -> 1 + f xs)) xs)

\begin{matrix} {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n}) {\texttt{ with}} & & \\\\\\ C_{2}^n (p_{1}, \ldots, p_{k}) {\texttt{->}} a {\texttt{ \textbar }} \operatorname{pm} & \Downarrow & {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n})\\\\\\ & & {\texttt{with} } \operatorname{pm} \end{matrix}

\begin{matrix} {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n}) {\texttt{ with}} & & \\\\\\ C_{2}^n (p_{1}, \ldots, p_{k}) {\texttt{->}} a {\texttt{ \textbar }} \operatorname{pm} & \Downarrow & {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n})\\\\\\ & & {\texttt{with} } \operatorname{pm} \end{matrix}

(match Cons (1, (Cons (2, Nil))) with | Cons (x, xs) -> 1 + (fix (fun f l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + f xs)) xs)

\begin{matrix} {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n}) {\texttt{ with}} & & \\\\\\ C_{1}^n (x_{1}, \ldots, x_{n}) {\texttt{->}} a {\texttt{ \textbar }} \ldots & \Downarrow & a [x_{1} := v_{1} ; \ldots ; x_{n} := v_{n}] \end{matrix}

\begin{matrix} {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n}) {\texttt{ with}} & & \\\\\\ C_{1}^n (x_{1}, \ldots, x_{n}) {\texttt{->}} a {\texttt{ \textbar }} \ldots & \Downarrow & a [x_{1} := v_{1} ; \ldots ; x_{n} := v_{n}] \end{matrix}

1 + (fix (fun f l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + f xs)) (Cons (2, Nil))

\begin{matrix} {\texttt{fix}}^2 v_{1} v_{2} & \rightsquigarrow & v_{1} \left( {\texttt{fix}}^2 v_{1} \right) v_{2}\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

\begin{matrix} {\texttt{fix}}^2 v_{1} v_{2} & \rightsquigarrow & v_{1} \left( {\texttt{fix}}^2 v_{1} \right) v_{2}\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

1 + (fun f l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + f xs)) (fix (fun f l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + f xs)) (Cons (2, Nil))

\begin{matrix} \left( {\texttt{fun }} x {\texttt{->}} a \right) v & \rightsquigarrow & a [x := v]\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

\begin{matrix} \left( {\texttt{fun }} x {\texttt{->}} a \right) v & \rightsquigarrow & a [x := v]\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

1 + (fun l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + (fix (fun f l -> match l with
| Nil -> 0 | Cons (x, xs) -> 1 + f xs)) xs))
(Cons (2, Nil))

\begin{matrix} \left( {\texttt{fun }} x {\texttt{->}} a \right) v & \rightsquigarrow & a [x := v]\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

\begin{matrix} \left( {\texttt{fun }} x {\texttt{->}} a \right) v & \rightsquigarrow & a [x := v]\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

1 + (match Cons (2, Nil) with | Nil -> 0 | Cons (x, xs) -> 1 + (fix (fun f l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + f xs)) xs))

\begin{matrix} {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n}) {\texttt{ with}} & & \\\\\\ C_{2}^n (p_{1}, \ldots, p_{k}) {\texttt{->}} a {\texttt{ \textbar }} \operatorname{pm} & \rightsquigarrow & {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n})\\\\\\ & & {\texttt{with} } \operatorname{pm}\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

\begin{matrix} {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n}) {\texttt{ with}} & & \\\\\\ C_{2}^n (p_{1}, \ldots, p_{k}) {\texttt{->}} a {\texttt{ \textbar }} \operatorname{pm} & \rightsquigarrow & {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n})\\\\\\ & & {\texttt{with} } \operatorname{pm}\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

1 + (match Cons (2, Nil) with | Cons (x, xs) -> 1 + (fix (fun f l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + f xs)) xs)

\begin{matrix} {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n}) {\texttt{ with}} & & \\\\\\ C_{1}^n (x_{1}, \ldots, x_{n}) {\texttt{->}} a {\texttt{ \textbar }} \ldots & \Downarrow & a [x_{1} := v_{1} ; \ldots ; x_{n} := v_{n}]\\\\\\ & & \end{matrix}

\begin{matrix} {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n}) {\texttt{ with}} & & \\\\\\ C_{1}^n (x_{1}, \ldots, x_{n}) {\texttt{->}} a {\texttt{ \textbar }} \ldots & \rightsquigarrow & a [x_{1} \:= v_{1} ; \ldots ; x_{n} := v_{n}]\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

1 + (1 + (fix (fun f l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + f xs)) Nil)

\begin{matrix} {\texttt{fix}}^2 v_{1} v_{2} & \rightsquigarrow & v_{1} \left( {\texttt{fix}}^2 v_{1} \right) v_{2}\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}'\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

\begin{matrix} {\texttt{fix}}^2 v_{1} v_{2} & \rightsquigarrow & v_{1} \left( {\texttt{fix}}^2 v_{1} \right) v_{2}\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}'\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

1 + (1 + (fun f l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + f xs) (fix (fun f l ->
match l with | Nil -> 0 | Cons (x, xs) -> 1 + f xs)) Nil)

\begin{matrix} \left( {\texttt{fun }} x {\texttt{->}} a \right) v & \rightsquigarrow & a [x := v]\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}'\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

\begin{matrix} \left( {\texttt{fun }} x {\texttt{->}} a \right) v & \rightsquigarrow & a [x := v]\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}'\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

1 + (1 + (fun l -> match l with | Nil -> 0 | Cons (x, xs) -> 1 + (fix (fun f l ->
match l with | Nil -> 0 | Cons (x, xs) -> 1 + f xs)) xs) Nil)

\begin{matrix} \left( {\texttt{fun }} x {\texttt{->}} a \right) v & \rightsquigarrow & a [x := v]\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}'\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

\begin{matrix} \left( {\texttt{fun }} x {\texttt{->}} a \right) v & \rightsquigarrow & a [x := v]\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}'\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

1 + (1 + (match Nil with | Nil -> 0 | Cons (x, xs) -> 1 + (fix (fun f l -> match l with
| Nil -> 0 | Cons (x, xs) -> 1 + f xs)) xs))

\begin{matrix} {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n}) {\texttt{ with}} & & \\\\\\ C_{1}^n (x_{1}, \ldots, x_{n}) {\texttt{->}} a {\texttt{ \textbar }} \ldots & \rightsquigarrow & a [x_{1} \:= v_{1} ; \ldots ; x_{n} := v_{n}]\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}'\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

\begin{matrix} {\texttt{match }} C_{1}^n (v_{1}, \ldots, v_{n}) {\texttt{ with}} & & \\\\\\ C_{1}^n (x_{1}, \ldots, x_{n}) {\texttt{->}} a {\texttt{ \textbar }} \ldots & \rightsquigarrow & a [x_{1} \:= v_{1} ; \ldots ; x_{n} := v_{n}]\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}'\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

1 + (1 + 0)

\begin{matrix} f^n v_{1} \ldots v_{n} & \rightsquigarrow & f (v_{1}, \ldots, v_{n})\\\\\\ a_{1} a_{2} & \Downarrow & a_{1} a_{2}' \end{matrix}

1 + 1

\begin{matrix} f^n v_{1} \ldots v_{n} & \Downarrow & f (v_{1}, \ldots, v_{n}) \end{matrix}

2

2 Language and rules of the untyped \lambda-calculus

• First, let’s forget about types.

• Next, let’s introduce a shortcut:

  • We write \lambda x.a for fun x->a, \lambda x y.a for fun x y->a, etc.

• Let’s forget about all other constructions, only fun and variables.

• The real \lambda-calculus has a more general reduction:

  \begin{matrix} \left( {\texttt{fun }} x {\texttt{->}} a_{1} \right) a_{2} & \rightsquigarrow & a_{1} [x := a_{2}] \end{matrix}

  (called \beta-reduction) and uses bound variable renaming (called \alpha-conversion), or some other trick, to avoid variable capture. But let’s not over-complicate things.

  • We will look into the \beta-reduction rule in the laziness lecture.
  • Why is \beta-reduction more general than the rule we use?

3 Booleans

• Alonzo Church introduced \lambda-calculus to encode logic.
• There are multiple ways to encode various sorts of data in \lambda-calculus. Not all of them make sense in a typed setting, i.e. the straightforward encode/decode functions do not type-check for them.
• Define c_true=\lambda x y.x and c_false=\lambda x y.y.
• Define c_and=\lambda x y.x y {\texttt{c\_false}}. Check that it works!
  • I.e. that c_and c_true c_true = c_true,otherwise c_and a b = c_false.

let ctrue = fun x y -> x‘‘True’’ is projection on the first argument.let cfalse = fun x y -> yAnd ‘‘false’’ on the second argument.let cand = fun x y -> x y cfalseIf one is false, then return false.let encodebool b = if b then ctrue else cfalselet decodebool c = c true falseTest the functions in the toplevel.

• Define c_or and c_not yourself!

4 If-then-else and pairs

• We will just use the OCaml syntax from now.

let ifthenelse = fun b -> bBooleans select the argument!

Remember to play with the functions in the toplevel.

let cpair m n = fun x -> x m nWe couple thingslet cfirst = fun p -> p ctrueby passing them together.let csecond = fun p -> p cfalseCheck that it works!

let encodepair encfst encsnd (a, b) = cpair (encfst a) (encsnd b)let decodepair defst desnd c = c (fun x y -> defst x, desnd y)let decodeboolpair c = decodepair decodebool decodebool c

• We can define larger tuples in the same manner:

  let ctriple l m n = fun x -> x l m n

5 Pair-encoded natural numbers

• Our first encoding of natural numbers is as the depth of nested pairs whose rightmost leaf is \lambda x.x and whose left elements are c_false.

let pn0 = fun x -> xStart with the identity function.let pnsucc n = cpair cfalse nStack another pair.let pnpred = fun x -> x cfalse[Explain these functions.]let pniszero = fun x -> x ctrue

We program in untyped lambda calculus as an exercise, and we need encoding / decoding to verify our exercises, so using “magic” for encoding / decoding is “fair game”.

let rec encodepnat n =We use Obj.magic to forget types. if n <= 0 then Obj.magic pn0 else pnsucc (Obj.magic (encodepnat (n-1)))Disregarding types,let rec decodepnat pn =these functions are straightforward! if decodebool (pniszero pn) then 0 else 1 + decodepnat (pnpred (Obj.magic pn))

6 Church numerals (natural numbers in Ch. enc.)

• Do you remember our function power f n? We will use its variant for a different representation of numbers:

let cn0 = fun f x -> xThe same as c_false.let cn1 = fun f x -> f xBehaves like identity.let cn2 = fun f x -> f (f x)let cn3 = fun f x -> f (f (f x))

• This is the original Alonzo Church encoding.

let cnsucc = fun n f x -> f (n f x)

• Define addition, multiplication, comparing to zero, and the predecesor function “-1” for Church numerals.
• Turns out even Alozno Church couldn’t define predecesor right away! But try to make some progress before you turn to the next slide.
  • His student Stephen Kleene found it.

let rec encodecnat n f = if n <= 0 then (fun x -> x) else f -| encodecnat (n-1) flet decodecnat n = n ((+) 1) 0let cn7 f x = encodecnat 7 f xWe need to \eta-expand these definitionslet cn13 f x = encodecnat 13 f xfor type-system reasons.(Because OCaml allows side-effects.)let cnadd = fun n m f x -> n f (m f x)Put n of f in front.let cnmult = fun n m f -> n (m f)Repeat n timesputting m of f in front.let cnprev n =
fun f x ->This is the ‘‘Church numeral signature’‘. nThe only thing we have is an n-step loop. (fun g v -> v (g f))We need sth that operates on f. (fun z->x)We need to ignore the innermost step.
(fun z->z)We’ve build a ‘‘machine’’ not results – start the machine.

cn_is_zero left as an exercise.

decodecnat (cn_prev cn3)

\Downarrow

(cn_prev cn3) ((+) 1) 0

\Downarrow

(fun f x -> cn3 (fun g v -> v (g f)) (fun z->x)
(fun z->z)) ((+) 1) 0

\Downarrow

((fun f x -> f (f (f x))) (fun g v -> v (g ((+) 1))) (fun z->0) (fun z->z))

\Downarrow

((fun g v -> v (g ((+) 1))) ((fun g v -> v (g ((+) 1))) ((fun g v -> v (g ((+) 1))) (fun z->0)))) (fun z->z))

\Downarrow

((fun z->z) (((fun g v -> v (g ((+) 1))) ((fun g v -> v (g ((+) 1))) (fun z->0)))) ((+) 1)))

\Downarrow

(fun g v -> v (g ((+) 1))) ((fun g v -> v (g ((+) 1))) (fun z->0)) ((+) 1)

\Downarrow

((+) 1) ((fun g v -> v (g ((+) 1))) (fun z->0) ((+) 1))

\Downarrow

((+) 1) (((+) 1) ((fun z->0) ((+) 1)))

\Downarrow

((+) 1) (((+) 1) (0))

\Downarrow

((+) 1) 1

\Downarrow

2

7 Recursion: Fixpoint Combinator

• Turing’s fixpoint combinator: \Theta = (\lambda x y.y (x x y)) (\lambda x y.y (x x y))

  \begin{matrix} N & = & \Theta F\\\\\\ & = & (\lambda x y.y (x x y)) (\lambda x y.y (x x y)) F\\\\\\ & =_{\rightarrow \rightarrow} & F ((\lambda x y.y (x x y)) (\lambda x y.y (x x y)) F)\\\\\\ & = & F (\Theta F) = F N \end{matrix}

• Curry’s fixpoint combinator: \boldsymbol{Y}= \lambda f. (\lambda x.f (x x)) (\lambda x.f (x x))

  \begin{matrix} N & = & \boldsymbol{Y}F\\\\\\ & = & (\lambda f. (\lambda x.f (x x)) (\lambda x.f (x x))) F\\\\\\ & =_{\rightarrow} & (\lambda x.F (x x)) (\lambda x.F (x x))\\\\\\ & =_{\rightarrow} & F ((\lambda x.F (x x)) (\lambda x.F (x x)))\\\\\\ & =_{\leftarrow} & F ((\lambda f. (\lambda x.f (x x)) (\lambda x.f (x x))) F)\\\\\\ & = & F (\boldsymbol{Y}F) = F N \end{matrix}

• Call-by-value fixpoint combinator: \lambda f' . (\lambda f x.f' (f f) x) (\lambda f x.f' (f f) x)

  \begin{matrix} N & = & \operatorname{fix}F\\\\\\ & = & (\lambda f' . (\lambda f x.f' (f f) x) (\lambda f x.f' (f f) x)) F\\\\\\ & =_{\rightarrow} & (\lambda f x.F (f f) x) (\lambda f x.F (f f) x)\\\\\\ & =_{\rightarrow} & \lambda x.F ((\lambda f x.F (f f) x) (\lambda f x.F (f f) x)) x\\\\\\ & =_{\leftarrow} & \lambda x.F ((\lambda f' . (\lambda f x.f' (f f) x) (\lambda f x.f' (f f) x)) F) x\\\\\\ & = & \lambda x.F (\operatorname{fix}F) x = \lambda x.F N x\\\\\\ & =_{\eta} & F N \end{matrix}

• The \lambda-terms we have seen above are fixpoint combinators – means inside \lambda-calculus to perform recursion.

• What is the problem with the first two combinators?

  \begin{matrix} \Theta F & \rightsquigarrow \rightsquigarrow & F ((\lambda x y.y (x x y)) (\lambda x y.y (x x y)) F)\\\\\\ & \rightsquigarrow \rightsquigarrow & F (F ((\lambda x y.y (x x y)) (\lambda x y.y (x x y)) F))\\\\\\ & \rightsquigarrow \rightsquigarrow & F (F (F ((\lambda x y.y (x x y)) (\lambda x y.y (x x y)) F)))\\\\\\ & \rightsquigarrow \rightsquigarrow & \ldots \end{matrix}

• Recall the distinction between expressions and values from the previous lecture Computation.

• The reduction rule for \lambda-calculus is just meant to determine which expressions are considered “equal” – it is highly non-deterministic, while on a computer, computation needs to go one way or another.

• Using the general reduction rule of \lambda-calculus, for a recursive definition, it is always possible to find an infinite reduction sequence (which means that you couldn’t complain when a nasty \lambda-calculus compiler generates infinite loops for all recursive definitions).

  • Why?

• Therefore, we need more specific rules. For example, most languages use \left( {\texttt{fun }} x {\texttt{->}} a \right) v \rightsquigarrow a [x := v], which is called call-by-value, or eager computation (because the program eagerly computes the arguments before starting to compute the function). (It’s exactly the rule we introduced in Computation lecture.)

• What happens with call-by-value fixpoint combinator?

  \begin{matrix} \operatorname{fix}F & \rightsquigarrow & (\lambda f x.F (f f) x) (\lambda f x.F (f f) x)\\\\\\ & \rightsquigarrow & \lambda x.F ((\lambda f x.F (f f) x) (\lambda f x.F (f f) x)) x \end{matrix}

  Voila – if we use \left( {\texttt{fun }} x {\texttt{->}} a \right) v \rightsquigarrow a [x := v] as the rulerather than \left( {\texttt{fun }} x {\texttt{->}} a_{1} \right) a_{2} \rightsquigarrow a_{1} [x := a_{2}], the computation stops. Let’s compute the function on some input:

  \begin{matrix} \operatorname{fix}F v & \rightsquigarrow & (\lambda f x.F (f f) x) (\lambda f x.F (f f) x) v\\\\\\ & \rightsquigarrow & (\lambda x.F ((\lambda f x.F (f f) x) (\lambda f x.F (f f) x)) x) v\\\\\\ & \rightsquigarrow & F ((\lambda f x.F (f f) x) (\lambda f x.F (f f) x)) v\\\\\\ & \rightsquigarrow & F (\lambda x.F ((\lambda f x.F (f f) x) (\lambda f x.F (f f) x)) x) v\\\\\\ & \rightsquigarrow & \text{depends on } F \end{matrix}

• Why the name fixpoint? If you look at our derivations, you’ll see that they show what in math can be written as x = f (x). Such values x are called fixpoints of f. An arithmetic function can have several fixpoints, for example f (x) = x^2 (which xes are fixpoints?) or no fixpoints, for example f (x) = x + 1.

• When you define a function (or another object) by recursion, it has very similar meaning: there is a name that is on both sides of =.

• In \lambda-calculus, there are functions like \Theta and \boldsymbol{Y}, that take any function as an argument, and return its fixpoint.

• We turn a specification of a recursive object into a definition, by solving it with respect to the recurring name: deriving x = f (x) where x is the recurring name. We then have x =\operatorname{fix} (f).

• Let’s walk through it for the factorial function (we omit the prefix cn_ – could be pn_ if pn1 was used instead of cn1 – for numeric functions, and we shorten if_then_else into if_t_e):

  \begin{matrix} {\texttt{fact}} n & = & {\texttt{if\_t\_e}} \left( {\texttt{is\_zero}} n \right) {\texttt{cn1}} \left( {\texttt{mult}} n \left( {\texttt{fact}} \left( {\texttt{pred}} n \right) \right) \right)\\\\\\ {\texttt{fact}} & = & \lambda n. {\texttt{if\_t\_e}} \left( {\texttt{is\_zero}} n \right) {\texttt{cn1}} \left( {\texttt{mult}} n \left( {\texttt{fact}} \left( {\texttt{pred}} n \right) \right) \right)\\\\\\ {\texttt{fact}} & = & \left( \lambda f n. {\texttt{if\_t\_e}} \left( {\texttt{is\_zero}} n \right) {\texttt{cn1}} \left( {\texttt{mult}} n \left( f \left( {\texttt{pred}} n \right) \right) \right) \right) {\texttt{fact}}\\\\\\ {\texttt{fact}} & = & \operatorname{fix} \left( \lambda f n. {\texttt{if\_t\_e}} \left( {\texttt{is\_zero}} n \right) {\texttt{cn1}} \left( {\texttt{mult}} n \left( f \left( {\texttt{pred}} n \right) \right) \right) \right) \end{matrix}

  The last specification is a valid definition: we just give a name to a (ground, a.k.a. closed) expression.

• We have seen how fix works already!

  • Compute fact cn2.

• What does fix (fun x -> cn_succ x) mean?

8 Encoding of Lists and Trees

• A list is either empty, which we often call Empty or Nil, or it consists of an element followed by another list (called “tail”), the other case often called Cons.

• Define nil= \lambda x y.y and consH T = \lambda x y.x H T.

• Add numbers stored inside a list:

  \begin{matrix} {\texttt{addlist}} l & = & l \left( \lambda h t. {\texttt{cn\_add}} h \left( {\texttt{addlist}} t \right) \right) {\texttt{cn0}} \end{matrix}

  To make a proper definition, we need to apply \operatorname{fix} to the solution of above equation.

  \begin{matrix} {\texttt{addlist}} & = & \operatorname{fix} \left( \lambda f l.l \left( \lambda h t. {\texttt{cn\_add}} h (f t) \right) {\texttt{cn0}} \right) \end{matrix}

• For trees, let’s use a different form of binary trees than so far: instead of keeping elements in inner nodes, we will keep elements in leaves.

• Define leafn = \lambda x y.x n and nodeL R = \lambda x y.y L R.

• Add numbers stored inside a tree:

  \begin{matrix} {\texttt{addtree}} t & = & t (\lambda n.n) \left( \lambda l r. {\texttt{cn\_add}} \left( {\texttt{addtree}} l \right) \left( {\texttt{addtree}} r \right) \right) \end{matrix}

  and, in solved form:

  \begin{matrix} {\texttt{addtree}} & = & \operatorname{fix} \left( \lambda f t.t (\lambda n.n) \left( \lambda l r. {\texttt{cn\_add}} (f l) (f r) \right) \right) \end{matrix}

let nil = fun x y -> ylet cons h t = fun x y -> x h tlet addlist l =
fix (fun f l -> l (fun h t -> cnadd h (f t)) cn0) l;;decodecnat
(addlist (cons cn1 (cons cn2 (cons cn7 nil))));;let leaf n = fun x y -> x nlet node l r = fun x y -> y l rlet addtree t = fix (fun f t -> t (fun n -> n) (fun l r -> cnadd (f l) (f r)) ) t;;decodecnat (addtree (node (node (leaf cn3) (leaf cn7)) (leaf cn1)));;

• Observe a regularity: when we encode a variant type with n variants, for each variant we define a function that takes n arguments.

• If the kth variant C_{k} has m_{k} parameters, then the function c_{k} that encodes it will have the form:

  C_{k} (v_{1}, \ldots, v_{m_{k}}) \sim c_{k} v_{1} \ldots v_{m_{k}} = \lambda x_{1} \ldots x_{n} .x_{k} v_{1} \ldots v_{m_{k}}

• The encoded variants serve as a shallow pattern matching with guaranteed exhaustiveness: kth argument corresponds to kth branch of pattern matching.

9 Looping Recursion

• Let’s come back to numbers defined as lengths lists and define addition:

let pnadd m n = fix (fun f m n -> ifthenelse (pniszero m) n (pnsucc (f (pnpred m) n)) ) m n;;decodepnat (pnadd pn3 pn3);;

• Oops… OCaml says:Stack overflow during evaluation (looping recursion?).
• What is wrong? Nothing as far as \lambda-calculus is concerned. But OCaml and F# always compute arguments before calling a function. By definition of fix, f corresponds to recursively calling pn_add. Therefore,(pnsucc (f (pnpred m) n)) will be called regardless of what(pniszero m) returns!
• Why addlist and addtree work?
• addlist and addtree work because their recursive calls are “guarded” by corresponding fun. What is inside of fun is not computed immediately, only when the function is applied to argument(s).
• To avoid looping recursion, you need to guard all recursive calls. Besides putting them inside fun, in OCaml or F# you can also put them in branches of a match clause, as long as one of the branches does not have unguarded recursive calls!
• The trick to use with functions like if_then_else, is to guard their arguments with fun x ->, where x is not used, and apply the result of if_then_else to some dummy value.
  • In OCaml or F# we would guard by fun () ->, and then apply to (), but we do not have datatypes like unit in \lambda-calculus.

let pnadd m n = fix (fun f m n -> (ifthenelse (pniszero m) (fun x -> n) (fun x -> pnsucc (f (pnpred m) n))) id ) m n;;decodepnat (pnadd pn3 pn3);;decodepnat (pnadd pn3 pn7);;

10 In-class Work and Homework

Define (implement) and verify: 1. c_or and c_not; 1. exponentiation for Church numerals; 1. is-zero predicate for Church numerals; 1. even-number predicate for Church numerals; 1. multiplication for pair-encoded natural numbers; 1. factorial n! for pair-encoded natural numbers. 1. Construct \lambda-terms m_{0}, m_{1}, \ldots such that for all n one has:

\begin{matrix} m_{0} & = & x \\\\\\ m_{n + 1} & = & m_{n + 2} m_{n} \end{matrix}

(where equality is after performing \beta-reductions). 1. Define (implement) and verify a function computing: the length of a list (in Church numerals); 1. cn_max – maximum of two Church numerals; 1. the depth of a tree (in Church numerals). 1. Representing side-effects as an explicitly “passed around” state value, write combinators that represent the imperative constructs: 1. for…to… 1. for…downto… 1. while…do… 1. do…while… 1. repeat…until…

Rather than writing a \lambda-term using the encodings that we’ve learnt, just implement the functions in OCaml / F#, using built-in int and bool types. You can use let rec instead of fix. * For example, in exercise (a), write a function let rec for_to f beg_i end_i s =… where f takes arguments i ranging from beg_i to end_i, state s at given step, and returns state s at next step; the for_to function returns the state after the last step. * And in exercise (c), write a function let rec while_do p f s =… where both p and f take state s at given step, and if p s returns true, then f s is computed to obtain state at next step; the while_do function returns the state after the last step.

Do not use the imperative features of OCaml and F#, we will not even cover them in this course!

Although we will not cover them, it is instructive to see the implementation using the imperative features, to better understand what is actually required of a solution to the last exercise.

1. let forto f begi endi s = let s = ref s in for i = begi to endi do
   s := f i !s done; !s
2. let fordownto f begi endi s = let s = ref s in for i = begi downto endi do s := f i !s done; !s
3. let whiledo p f s = let s = ref s in while p !s do s := f !s done;
   !s
4. let dowhile p f s = let s = ref (f s) in while p !s do s := f !s
   done; !s
5. let repeatuntil p f s = let s = ref (f s) in while not (p !s) do s := f !s done; !s

Functional Programming

Functions

Exercise 1: Define (implement) and test on a couple of examples functions corresponding to / computing:

1. *c_or* and *c_not*;
2. exponentiation for Church numerals;
3. is-zero predicate for Church numerals;
4. even-number predicate for Church numerals;
5. multiplication for pair-encoded natural numbers;
6. factorial n! for pair-encoded natural numbers.
7. the length of a list (in Church numerals);
8. *cn_max* – maximum of two Church numerals;
9. the depth of a tree (in Church numerals).

Exercise 2: Representing side-effects as an explicitly “passed around” state value, write (higher-order) functions that represent the imperative constructs:

1. *for…to**…*
2. *for…downto**…*
3. *while…do**…*
4. *do…while**…*
5. *repeat…until**…*

Rather than writing a \lambda-term using the encodings that we’ve learnt, just implement the functions in OCaml / F#, using built-in int and bool types. You can use let rec instead of fix.

• For example, in exercise (a), write a function let rec *for_to f beg_i end_i s* =… where *f* takes arguments *i* ranging from *beg_i* to *end_i*, state *s* at given step, and returns state *s* at next step; the *for_to* function returns the state after the last step.
• And in exercise (c), write a function let rec *while_do p f s* =… where both *p* and *f* take state *s* at given step, and if *p s* returns true, then *f s* is computed to obtain state at next step; the *while_do* function returns the state after the last step.

Do not use the imperative features of OCaml and F#, we will not even cover them in this course!

Despite we will not cover them, it is instructive to see the implementation using the imperative features, to better understand what is actually required of a solution to this exercise.

1. let forto f begi endi s = let s = ref s in for i = begi to endi do
   s := f i !s done; !s
2. let fordownto f begi endi s = let s = ref s in for i = begi downto endi do s := f i !s done; !s
3. let whiledo p f s = let s = ref s in while p !s do s := f !s done;
   !s
4. let dowhile p f s = let s = ref (f s) in while p !s do s := f !s
   done; !s
5. let repeatuntil p f s = let s = ref (f s) in while not (p !s) do s := f !s done; !s

Lecture 5: Polymorphism & ADTs

Parametric types. Abstract Data Types.

Example: maps using red-black trees.

If you see any error on the slides, let me know!

1 Type Inference

We have seen the rules that govern the assignment of types to expressions, but how does OCaml guess what types to use, and when no correct types exist? It solves equations.

• Variables play two roles: of unknowns and of parameters.

  • Inside:

    # let f = List.hd;;
    val f : 'a list -> 'a

    'a is a parameter: it can become any type. Mathematically we write: f : \forall \alpha . \alpha \operatorname{list} \rightarrow \alpha – the quantified type is called a type scheme.

  • Inside:

    # let x = ref [];;
    val x : 'a list ref

    '_a is an unknown. It stands for a particular type like float or (int -> int), OCaml just doesn’t yet know the type.

  • OCaml only reports unknowns like '_a in inferred types for reasons not relevant to functional programming. When unknowns appear in inferred type against our expectations, \eta-expansion may help: writing let f x = expr x instead of let f = expr – for example:

    # let f = List.append [];;
    val f : 'a list -> 'a list = <fun>
    # let f l = List.append [] l;;
    val f : 'a list -> 'a list = <fun>

• A type environment specifies what names (corresponding to parameters and definitions) are available for an expression, because they were introduced above it, and it specifies their types.
• Type inference solves equations over unknowns. “What has to hold so that e : \tau in type environment \Gamma?”
  • If, for example, f : \forall \alpha . \alpha \operatorname{list} \rightarrow \alpha \in \Gamma, then for f : \tau we introduce \gamma \operatorname{list} \rightarrow \gamma = \tau for some fresh unknown \gamma.
  • For e_{1} e_{2} : \tau we introduce \beta = \tau and ask for e_{1} : \gamma \rightarrow \beta and e_{2} : \gamma, for some fresh unknowns \beta, \gamma.
  • For \operatorname{fun}x \rightarrow e : \tau we introduce \beta \rightarrow \gamma = \tau and ask for e : \gamma in environment \lbrace x : \beta \rbrace \cup \Gamma, for some fresh unknowns \beta, \gamma.
  • Case \operatorname{let}x = e_{1} \operatorname{in}e_{2} : \tau is different. One approach is to first solve the equations that we get by asking for e_{1} : \beta, for some fresh unknown \beta. Let’s say a solution \beta = \tau_{\beta} has been found, \alpha_{1} \ldots \alpha_{n} \beta_{1} \ldots \beta_{m} are the remaining unknowns in \tau_{\beta}, and \alpha_{1} \ldots \alpha_{n} are all that do not appear in \Gamma. Then we ask for e_{2} : \tau in environment \lbrace x : \forall \alpha_{1} \ldots \alpha_{n} . \tau_{\beta} \rbrace \cup \Gamma.
  • Remember that whenever we establish a solution \beta = \tau_{\beta} to an unknown \beta, it takes effect everywhere!
  • To find a type for e (in environment \Gamma), we pick a fresh unknown \beta and ask for e : \beta (in \Gamma).
• The “top-level” definitions for which the system infers types with variables are called polymorphic, which informally means “working with different shapes of data”.
  • This kind of polymorphism is called parametric polymorphism, since the types have parameters. A different kind of polymorphism is provided by object-oriented programming languages.

2 Parametric Types

• Polymorphic functions shine when used with polymorphic data types. In:

  type ’a mylist = Empty | Cons of ’a * ’a mylist

  we define lists that can store elements of any type 'a. Now:

  # let tail l =  match l with    | Empty -> invalidarg "tail"    | Cons 
  (, tl) -> tl;;      val tail : 'a mylist -> 'a mylist

  is a polymorphic function: works for lists with elements of any type.

• A parametric type like ’a mylist is not itself a data type but a family of data types: bool mylist, int mylist etc. are different types.

  • We say that the type int mylist instantiates the parametric type ’a mylist.

• In OCaml, the syntax is a bit confusing: type parameters precede type name. For example:

  type (’a, ’b) choice = Left of ’a | Right of ’b

  has two parameters. Mathematically we would write \operatorname{choice} (\alpha, \beta).

  • Functions do not have to be polymorphic:

    # let getint c =  match c with
        | Left i -> i
        | Right b -> if b then 1 else 0;;
    val getint : (int, bool) choice -> int

• In F#, we provide parameters (when more than one) after type name:

  type choice<'a,'b> = Left of 'a | Right of ’b

• In Haskell, we provide type parameters similarly to function arguments:

  data Choice a b = Left a | Right b

3 Type Inference, Formally

• A statement that an expression has a type in an environment is called a type judgement. For environment \Gamma = \lbrace x : \forall \alpha _{1} \ldots \alpha_{n} . \tau_{x} ; \ldots \rbrace, expression e and type \tau we write

  \[ e : \]

• We will derive the equations in one go using \llbracket \cdot \rrbracket, to be solved later. Besides equations we will need to manage introduced variables, using existential quantification.

• For local definitions we require to remember what constraints should hold when the definition is used. Therefore we extend type schemes in the environment to: \Gamma = \lbrace x : \forall \beta_{1} \ldots \beta_{m} [\exists \alpha_{1} \ldots \alpha_{n} .D] . \tau_{x} ; \ldots \rbrace where D are equations – keeping the variables \alpha_{1} \ldots \alpha _{n} introduced while deriving D in front.

  • A simpler form would be enough: \Gamma = \lbrace x : \forall \beta [\exists \alpha_{1} \ldots \alpha_{n} .D] . \beta ; \ldots \rbrace

\begin{matrix} \llbracket \Gamma \vdash x : \tau \rrbracket & = & \exists \overline{\beta'} \bar{\alpha}' . (D [\bar{\beta} \bar{\alpha} := \overline{\beta'} \bar{\alpha}'] \wedge \tau_{x} [\bar{\beta} \bar{\alpha} := \overline{\beta'} \bar{\alpha}'] \dot{=} \tau)\\\\\\ & & \text{where } \Gamma (x) = \forall \bar{\beta} [\exists \bar{\alpha} .D] . \tau_{x}, \overline{\beta'} \bar{\alpha}' \#\operatorname{FV} (\Gamma, \tau)\\\\\\ & & \\\\\\ \llbracket \Gamma \vdash \boldsymbol{\operatorname{fun}} x {\texttt{->}} e : \tau \rrbracket & = & \exists \alpha _{1} \alpha_{2} . (\llbracket \Gamma \lbrace x : \alpha_{1} \rbrace \vdash e : \alpha_{2} \rrbracket \wedge \alpha_{1} \rightarrow \alpha _{2} \dot{=} \tau),\\\\\\ & & \text{where } \alpha_{1} \alpha_{2} \#\operatorname{FV} (\Gamma, \tau)\\\\\\ & & \\\\\\ \llbracket \Gamma \vdash e_{1} e_{2} : \tau \rrbracket & = & \exists \alpha . (\llbracket \Gamma \vdash e_{1} : \alpha \rightarrow \tau \rrbracket \wedge \llbracket \Gamma \vdash e_{2} : \alpha \rrbracket), \alpha \#\operatorname{FV} (\Gamma, \tau)\\\\\\ & & \\\\\\ \llbracket \Gamma \vdash K e_{1} \ldots e_{n} : \tau \rrbracket & = & \exists \bar{\alpha}' . (\wedge_{i} \llbracket \Gamma \vdash e_{i} : \tau _{i} [\bar{\alpha} := \bar{\alpha}'] \rrbracket \wedge \varepsilon (\bar{\alpha}') \dot{=} \tau),\\\\\\ & & \text{w. } K \,:\, \forall \bar{\alpha} . \tau_{1} \times \ldots \times \tau_{n} \rightarrow \varepsilon (\bar{\alpha}), \bar{\alpha}' \#\operatorname{FV} (\Gamma, \tau)\\\\\\ & & \\\\\\ \llbracket \Gamma \vdash e : \tau \rrbracket & = & (\exists \beta .C) \wedge \llbracket \Gamma \lbrace x : \forall \beta [C] . \beta \rbrace \vdash e_{2} : \tau \rrbracket\\\\\\ e = \boldsymbol{\operatorname{let}} x = e_{1} \boldsymbol{\operatorname{in}} e_{2} & & \text{where } C = \llbracket \Gamma \vdash e_{1} : \beta \rrbracket\\\\\\ & & \\\\\\ \llbracket \Gamma \vdash e : \tau \rrbracket & = & (\exists \beta .C) \wedge \llbracket \Gamma \lbrace x : \forall \beta [C] . \beta \rbrace \vdash e_{2} : \tau \rrbracket\\\\\\ e = \boldsymbol{\operatorname{letrec}} x = e_{1} \boldsymbol{\operatorname{in}} e_{2} & & \text{where } C = \llbracket \Gamma \lbrace x : \beta \rbrace \vdash e_{1} : \beta \rrbracket\\\\\\ & & \\\\\\ \llbracket \Gamma \vdash e : \tau \rrbracket & = & \exists \alpha_{v} . \llbracket \Gamma \vdash e_{v} : \alpha_{v} \rrbracket \wedge_{i} \llbracket \Gamma \vdash p_{i} .e_{i} : \alpha_{v} \rightarrow \tau \rrbracket,\\\\\\ e = \boldsymbol{\operatorname{match}} e_{v} \boldsymbol{\operatorname{with}} \bar{c} & & \alpha_{v} \#\operatorname{FV} (\Gamma, \tau)\\\\\\ \bar{c} = p_{1} .e_{1} | \ldots |p_{n} .e_{n} & & \\\\\\ & & \\\\\\ \llbracket \Gamma, \Sigma \vdash p.e : \tau_{1} \rightarrow \tau_{2} \rrbracket & = & \llbracket \Sigma \vdash p \downarrow \tau_{1} \rrbracket \wedge \exists \bar{\beta} . \llbracket \Gamma \Gamma' \vdash e : \tau_{2} \rrbracket\\\\\\ & & \text{where } \exists \bar{\beta} \Gamma' \text{ is } \llbracket \Sigma \vdash p \uparrow \tau_{1} \rrbracket, \bar{\beta} \#\operatorname{FV} (\Gamma, \tau_{2})\\\\\\ & & \\\\\\ \llbracket \Sigma \vdash p \downarrow \tau_{1} \rrbracket & & \text{derives constraints on type of matched value}\\\\\\ & & \\\\\\ \llbracket \Sigma \vdash p \uparrow \tau_{1} \rrbracket & & \text{derives environment for pattern variables} \end{matrix}

• By \bar{\alpha} or \overline{\alpha_{i}} we denote a sequence of some length: \alpha_{1} \ldots \alpha_{n}
• By \wedge_{i} \varphi_{i} we denote a conjunction of \overline{\varphi_{i}}: \varphi_{1} \ldots \varphi_{n}.

3.1 Polymorphic Recursion

• Note the limited polymorphism of let rec f = … – we cannot use f polymorphically in its definition.
  • In modern OCaml we can bypass the problem if we provide type of f upfront: let rec f : ’a. ’a -> ’a list = …
  • where ’a. ’a -> ’a list stands for \forall \alpha . \alpha \rightarrow \alpha \operatorname{list}.
• Using the recursively defined function with different types in its definition is called polymorphic recursion.
• It is most useful together with irregular recursive datatypes where the recursive use has different type arguments than the actual parameters.

3.1.1 Polymorphic Rec: A list alternating between two types of elements

type (’x, ’o) alterning =| Stop| One of ’x * (’o, ’x) alterninglet rec tolist : ’x ’o ’a. (’x->’a) -> (’o->’a) -> (’x, ’o) alterning -> ’a list = fun x2a o2a -> function | Stop -> [] | One (x, rest) -> x2a x::tolist o2a x2a restlet tochoicelist alt = tolist (fun x->Left x) (fun o->Right o) altlet it = tochoicelist (One (1, One (“o”, One (2, One (“oo”, Stop)))))

3.1.2 Polymorphic Rec: Data-Structural Bootstrapping

type ’a seq = Nil | Zero of (’a * ’a) seq | One of ’a * (’a * ’a) seqWe store a list of elements in exponentially increasing chunks.let example = One (0, One ((1,2), Zero (One ((((3,4),(5,6)), ((7,8),(9,10))), Nil))))let rec cons : ’a. ’a -> ’a seq -> ’a seq = fun x -> functionAppending an element to the datastructure is like | Nil -> One (x, Nil)adding one to a binary number: 1+0=1 | Zero ps -> One (x, ps)1+…0=…1 | One (y, ps) -> Zero (cons (x,y) ps)1+…1=[…+1]0let rec lookup : ’a. int -> ’a seq -> ’a = fun i s -> match i, s withRather than returning None : 'a option | , Nil -> raise Notfoundwe raise exception, for convenience. | 0, One (x, ) -> x | i, One (, ps) -> lookup (i-1) (Zero ps) | i, Zero ps ->Random-Access lookup works let x, y = lookup (i / 2) ps inin logarithmic time – much faster than if i mod 2 = 0 then x else yin standard lists.

4 Algebraic Specification

• The way we introduce a data structure, like complex numbers or strings, in mathematics, is by specifying an algebraic structure.
• Algebraic structures consist of a set (or several sets, for so-called multisorted algebras) and a bunch of functions (aka. operations) over this set (or sets).
• A signature is a rough description of an algebraic structure: it provides sorts – names for the sets (in multisorted case) and names of the functions-operations together with their arity (and what sorts of arguments they take).
• We select a class of algebraic structures by providing axioms that have to hold. We will call such classes algebraic specifications.
  • In mathematics, a rusty name for some algebraic specifications is a variety, a more modern and name is algebraic category.
• Algebraic structures correspond to “implementations” and signatures to “interfaces” in programming languages.
• We will say that an algebraic structure implements an algebraic specification when all axioms of the specification hold in the structure.
• All algebraic specifications are implemented by multiple structures!
• We say that an algebraic structure does not have junk, when all its elements (i.e. elements in the sets corresponding to sorts) can be built using operations in its signature.
• We allow parametric types as sorts. In that case, strictly speaking, we define a family of algebraic specifications (a different specification for each instantiation of the parametric type).

4.1 Algebraic specifications: examples

• An algebraic specification can also use an earlier specification.
• In “impure” languages like OCaml and F# we allow that the result of any operation be an \operatorname{error}. In Haskell we could use Maybe.

5 Homomorphisms

• Mappings between algebraic structures with the same signature preserving operations.
• A homomorphism from algebraic structure (A, \lbrace f^A, g^A, \ldots \rbrace) to (B, \lbrace f^B, g^B, \ldots \rbrace) is a function h : A \rightarrow B such that h (f^A (a_{1}, \ldots, a_{n_{f}})) = f^B (h (a_{1}), \ldots, h (a_{n_{f}})) for all (a_{1}, \ldots, a_{n_{f}}), h (g^A (a_{1}, \ldots, a_{n_{g}})) = g^B (h (a_{1}), \ldots, h (a_{n_{g}})) for all (a_{1}, \ldots, a_{n_{g}}), …
• Two algebraic structures are isomorphic if there are homomorphisms h_{1} : A \rightarrow B, h_{2} : B \rightarrow A from one to the other and back, that when composed in any order form identity: \forall (b \in B) h_{1} (h_{2} (b)) = b, \forall (a \in A) h_{2} (h_{1} (a)) = a.
• An algebraic specification whose all implementations without junk are isomorphic is called “monomorphic”.
  • We usually only add axioms that really matter to us to the specification, so that the implementations have room for optimization. For this reason, the resulting specifications will often not be monomorphic in the above sense.

6 Example: Maps

7 Modules and interfaces (signatures): syntax

• In the ML family of languages, structures are given names by module bindings, and signatures are types of modules.
• From outside of a structure or signature, we refer to the values or types it provides with a dot notation: Module.value.
• Module (and module type) names have to start with a capital letter (in ML languages).
• Since modules and module types have names, there is a tradition to name the central type of a signature (the one that is “specified” by the signature), for brevity, t.
• Module types are often named with “all-caps” (all letters upper case).

module type MAP = sig type (’a, ’b) t val empty : (’a, ’b) t val member : ’a -> (’a, ’b) t -> bool val add : ’a -> ’b -> (’a, ’b) t -> (’a, ’b) t val remove : ’a -> (’a, ’b) t -> (’a, ’b) t val find : ’a -> (’a, ’b) t -> ’bendmodule ListMap : MAP = struct type (’a, ’b) t = (’a * ’b) list let empty = [] let member = List.memassoc let add k v m = (k, v)::m let remove = List.removeassoc let find = List.assocend

8 Implementing maps: Association lists

Let’s now build an implementation of maps from the ground up. The most straightforward implementation… might not be what you expected:

module TrivialMap : MAP = struct  type ('a, 'b) t =    | Empty    | Add of 'a 
\* 'b \* ('a, 'b) t    | Remove of 'a \* ('a, 'b) t          let empty = Empty 
 let rec member k m =    match m with      | Empty -> false      | Add 
(k2, , ) when k = k2 -> true      | Remove (k2, ) when k = k2 -> false 
     | Add (, , m2) -> member k m2      | Remove (, m2) -> member k m2 
 let add k v m = Add (k, v, m)  let remove k m = Remove (k, m)  let rec find k 
m =    match m with      | Empty -> raise Not_found      | Add (k2, v, ) 
when k = k2 -> v      | Remove (k2, ) when k = k2 -> raise Notfound    
  | Add (, , m2) -> find k m2      | Remove (, m2) -> find k m2 end

Here is an implementation based on association lists, i.e. on lists of key-value pairs.

module MyListMap : MAP = struct  type ('a, 'b) t = Empty | Add of 'a \* 'b \* 
('a, 'b) t  let empty = Empty  let rec member k m =    match m with      | 
Empty -> false      | Add (k2, , ) when k = k2 -> true      | Add (, , 
m2) -> member k m2  let rec add k v m =    match m with      | 
Empty -> Add (k, v, Empty)      | Add (k2, , m) when k = k2 -> Add (k, 
v, m)      | Add (k2, v2, m) -> Add (k2, v2, add k v m)

  let rec remove k m =    match m with      | Empty -> Empty      | Add 
(k2, , m) when k = k2 -> m      | Add (k2, v, m) -> Add (k2, v, remove 
k m)  let rec find k m =    match m with      | Empty -> raise Error      
| Add (k2, v, ) when k = k2 -> v      | Add (, , m2) -> find k m2 end

9 Implementing maps: Binary search trees

• Binary search trees are binary trees with elements stored at the interior nodes, such that elements to the left of a node are smaller than, and elements to the right bigger than, elements within a node.
• For maps, we store key-value pairs as elements in binary search trees, and compare the elements by keys alone.
• On average, binary search trees are fast because they use “divide-and-conquer” to search for the value associated with a key. (O (\log n) compl.)
  • In worst case they reduce to association lists.
• The simple polymorphic signature for maps is only possible with implementations based on some total order of keys because OCaml has polymorphic comparison (and equality) operators.
  • These operators work on elements of most types, but not on functions. They may not work in a way you would want though!
  • Our signature for polymorphic maps is not the standard approach because of the problem of needing the order of keys; it is just to keep things simple.

module BTreeMap : MAP = struct  type ('a, 'b) t = Empty | T of ('a, 'b) t \* 
'a \* 'b \* ('a, 'b) t  let empty = Empty  let rec member k m =‘‘Divide and 
conquer'' search through the tree.    match m with      | Empty -> false   
   | T (, k2, , ) when k = k2 -> true      | T (m1, k2, , ) when k < 
k2 -> member k m1      | T (, , , m2) -> member k m2  let rec add k v 
m =Searches the tree in the same way as `member`    match m withbut copies 
every node along the way.      | Empty -> T (Empty, k, v, Empty)      | T 
(m1, k2, , m2) when k = k2 -> T (m1, k, v, m2)      | T (m1, k2, v2, m2) 
when k < k2 -> T (add k v m1, k2, v2, m2)      | T (m1, k2, v2, 
m2) -> T (m1, k2, v2, add k v m2)

let rec splitrightmost m = (* A helper 
function, it does not belong *)
   match m with (* to the ‘‘exported'' signature.     *)
 | Empty -> raise Notfound      | T (Empty, k, v, Empty) -> k, v, 
EmptyWe remove one element,      | T (m1, k, v, m2) ->the one that is on 
the bottom right.        let rk, rv, rm = splitrightmost m2 in        rk, rv, 
T (m1, k, v, rm)

  let rec remove k m =    match m with      | Empty -> Empty      | T (m1, 
k2, , Empty) when k = k2 -> m1      | T (Empty, k2, , m2) when k = 
k2 -> m2      | T (m1, k2, , m2) when k = k2 ->        let rk, rv, rm 
= splitrightmost m1 in        T (rm, rk, rv, m2)      | T (m1, k2, v, m2) when 
k < k2 -> T (remove k m1, k2, v, m2)      | T (m1, k2, v, m2) -> 
T (m1, k2, v, remove k m2)  let rec find k m =    match m with      | 
Empty -> raise Notfound      | T (, k2, v, ) when k = k2 -> v      | T 
(m1, k2, , ) when k < k2 -> find k m1      | T (, , , m2) -> find 
k m2 end

10 Implementing maps: red-black trees

Based on Wikipedia http://en.wikipedia.org/wiki/Red-black_tree, Chris Okasaki’s “Functional Data Structures” and Matt Might’s excellent blog post http://matt.might.net/articles/red-black-delete/.

• Binary search trees are good when we encounter keys in random order, because the cost of operations is limited by the depth of the tree which is small relatively to the number of nodes…
• …unless the tree grows unbalanced achieving large depth (which means there are sibling subtrees of vastly different sizes on some path).
• To remedy it, we rebalance the tree while building it – i.e. while adding elements.
• In red-black trees we achieve balance by remembering one of two colors with each node, keeping the same length of each root-leaf path if only black nodes are counted, and not allowing a red node to have a red child.
  • This way the depth is at most twice the depth of a perfectly balanced tree with the same number of nodes.

10.1 B-trees of order 4 (2-3-4 trees)

How can we have perfectly balanced trees without worrying about having 2^k - 1 elements? 2-3-4 trees can store from 1 to 3 elements in each node and have 2 to 4 subtrees correspondingly. Lots of freedom!

To insert “25” into (“.” stand for leaves, ignored later)

we descend right, but it is a full node, so we move the middle up and split the remaining elements:

Now there is a place between 24 and 29: next to 29

To represent 2-3-4 tree as a binary tree with one element per node, we color the middle element of a 4-node, or the first element of 2-/3-node, black and make it the parent of its neighbor elements, and make them parents of the original subtrees. Turning this:

Red-black_tree_B-tree.png

into this Red-Black tree:

Red-black_tree_example.png

10.2 Red-Black trees, without deletion

• Invariant 1. No red node has a red child.
• Invariant 2. Every path from the root to an empty node contains the same number of black nodes.
• First we implement Red-Black tree based sets without deletion.
• The implementation proceeds almost exactly like for unbalanced binary search trees, we only need to restore invariants.
• By keeping balance at each step of constructing a node, it is enough to check locally (around the root of the subtree).
• For understandable implementation of deletion, we need to introduce more colors. See Matt Might’s post edited in a separate file.

type color = R | Btype 'a t = E | T of color \* 'a t \* 'a \* 'a tlet empty = 
Elet rec member x m =  match m withLike in unbalanced binary search tree.  | 
Empty -> false  | T (, , y, ) when x = y -> true  | T (, a, y, ) when 
x < y -> member x a  | T (, , , b) -> member x blet balance = 
functionRestoring the invariants.  | B,T (R,T (R,a,x,b),y,c),z,dOn next 
figure: left,  | B,T (R,a,x,T (R,b,y,c)),z,dtop,  | B,a,x,T (R,T 
(R,b,y,c),z,d)bottom,  | B,a,x,T (R,b,y,T (R,c,z,d))right,    -> T (R,T 
(B,a,x,b),y,T (B,c,z,d))center tree.  | color,a,x,b -> T (color,a,x,b)We 
allow red-red violation for now.

let insert x s =  let rec ins = functionLike in unbalanced binary search tree, 
   | E -> T (R,E,x,E)but fix violation above created node.    | T 
(color,a,y,b) as s ->      if x<y then balance (color,ins a,y,b)      
else if x>y then balance (color,a,y,ins b)      else s in
  match ins s with (* We could still have red-red violation at root, *)
  | T (,a,y,b) -> T (B,a,y,b) (* fixed by coloring it black. *)
  | E -> failwith "insert: impossible"

11 Homework

1. Derive the equations and solve them to find the type for:

   let cadr l = List.hd (List.tl l) in cadr (1::2::[]), cadr (true::false::[])

   in environ. \Gamma = \left\lbrace \text{{\textcolor{green}{List}}{\textcolor{blue}{.}}{\textcolor{brown}{hd}}} : \forall \alpha . \alpha \operatorname{list} \rightarrow \alpha ; \text{{\textcolor{green}{List}}{\textcolor{blue}{.}}{\textcolor{brown}{tl}}} : \forall \alpha . \alpha \operatorname{list} \rightarrow \alpha \operatorname{list} \right\rbrace. You can take “shortcuts” if it is too many equations to write down.

2. What does it mean that an implementation has junk (as an algebraic structure for a given signature)? Is it bad?

3. Define a monomorphic algebraic specification (other than, but similar to, \operatorname{nat}_{p} or \operatorname{string}_{p}, some useful data type).

4. Discuss an example of a (monomorphic) algebraic specification where it would be useful to drop some axioms (giving up monomorphicity) to allow more efficient implementations.

5. Does the example ListMap meet the requirements of the algebraic specification for maps? Hint: here is the definition of List.removeassoc; compare a x equals 0 if and only if a = x.

   let rec removeassoc x = function  | [] -> []  | (a, b as pair) :: l ->
         if compare a x = 0 then l else pair :: removeassoc x l

6. Trick question: what is the computational complexity of ListMap or TrivialMap?

7. * The implementation MyListMap is inefficient: it performs a lot of copying and is not tail-recursive. Optimize it (without changing the type definition).

8. Add (and specify) \operatorname{isEmpty}: (\alpha, \beta) \operatorname{map} \rightarrow \operatorname{bool} to the example algebraic specification of maps without increasing the burden on its implementations (i.e. without affecting implementations of other operations). Hint: equational reasoning might be not enough; consider an equivalence relation \approx meaning “have the same keys”, defined and used just in the axioms of the specification.

9. Design an algebraic specification and write a signature for first-in-first-out queues. Provide two implementations: one straightforward using a list, and another one using two lists: one for freshly added elements providing efficient queueing of new elements, and “reversed” one for efficient popping of old elements.

10. Design an algebraic specification and write a signature for sets. Provide two implementations: one straightforward using a list, and another one using a map into the unit type.

11. (Ex. 2.2 in Chris Okasaki “Purely Functional Data Structures”) In the worst case, member performs approximately 2 d comparisons, where d is the depth of the tree. Rewrite member to take no mare than d + 1 comparisons by keeping track of a candidate element that might be equal to the query element (say, the last element for which < returned false) and checking for equality only when you hit the bottom of the tree.

12. (Ex. 3.10 in Chris Okasaki “Purely Functional Data Structures”) The balance function currently performs several unnecessary tests: when e.g.  ins recurses on the left child, there are no violations on the right child.

    1. Split balance into lbalance and rbalance that test for violations of left resp. right child only. Replace calls to balance appropriately.
    2. One of the remaining tests on grandchildren is also unnecessary. Rewrite ins so that it never tests the color of nodes not on the search path.

13. * Implement maps (i.e. write a module for the map signature) based on AVL trees. See http://en.wikipedia.org/wiki/AVL_tree.

Functional Programming

Type Inference

Abstract Data Types

Exercise 1: Derive the equations and solve them to find the type for:

let cadr l = List.hd (List.tl l) in cadr (1::2::[]), cadr (true::false::[])

in environment \Gamma = \left\lbrace \text{{\textcolor{green}{List}}{\textcolor{blue}{.}}{\textcolor{brown}{hd}}} : \forall \alpha . \alpha \operatorname{list} \rightarrow \alpha ; \text{{\textcolor{green}{List}}{\textcolor{blue}{.}}{\textcolor{brown}{tl}}} : \forall \alpha . \alpha \operatorname{list} \rightarrow \alpha \operatorname{list} \right\rbrace. You can take “shortcuts” if it is too many equations to write down.

Exercise 2: Terms t_{1}, t_{2}, \ldots \in T (\Sigma, X) are built out of variables x, y, \ldots \in X and function symbols f, g, \ldots \in \Sigma the way you build values out of functions:

• X \subset T (\Sigma, X) – variables are terms; usually an infinite set,
• for terms t_{1}, \ldots, t_{n} \in T (\Sigma, X) and a function symbol f \in \Sigma _{n} of arity n,f (t_{1}, \ldots, t_{n}) \in T (\Sigma, X) – bigger terms arise from applying function symbols to smaller terms; \Sigma = \dot{\cup}_{n} \Sigma _{n} is called a signature.

In OCaml, we can define terms as: type term = V of string | T of string term list5mm, where for example V(“x”) is a variable x and T(“f”, [V(“x”); V(“y”)]) is the term f (x, y).*

By substitutions* \sigma, \rho, \ldots we mean finite sets of variable, term pairs which we can write as \lbrace x_{1} \mapsto t_{1}, \ldots, x_{k} \mapsto t_{k} \rbrace or [x_{1} := t_{1} ; \ldots ; x_{k} := t_{k}], but also functions from terms to terms \sigma : T (\Sigma, X) \rightarrow T (\Sigma, X) related to the pairs as follows: if \sigma = \lbrace x_{1} \mapsto t_{1}, \ldots, x_{k} \mapsto t_{k} \rbrace, then*

• \sigma (x_{i}) = t_{i} for x_{i} \in \lbrace x_{1}, \ldots, x_{k} \rbrace,
• \sigma (x) = x for x \in X\backslash \lbrace x_{1}, \ldots, x_{k} \rbrace,
• \sigma (f (t_{1}, \ldots, t_{n})) = f (\sigma (t_{1}), \ldots, \sigma (t_{n})).

In OCaml, we can define substitutions \sigma as: type subst = (string term) list, together with a function apply : subst -> term -> term which computes \sigma (\cdot).*

We say that a substitution \sigma is more general* than all substitutions \rho \circ \sigma, where (\rho \circ \sigma) (x) = \rho (\sigma (x)). In type inference, we are interested in most general solutions: the less general type judgement \text{{\textcolor{green}{List}}{\textcolor{blue}{.}}{\textcolor{brown}{hd}}} : \operatorname{int}\operatorname{list} \rightarrow \operatorname{int}, although valid, is less useful than \text{{\textcolor{green}{List}}{\textcolor{blue}{.}}{\textcolor{brown}{hd}}} : \forall \alpha . \alpha \operatorname{list} \rightarrow \alpha because it limits the usage of List.hd.*

A unification problem* is a finite set of equations S = \lbrace s_{1} =^? t_{1}, \ldots, s_{n} =^? t_{n} \rbrace which we can also write as s_{1} \dot{=} t_{1} \wedge \ldots \wedge s_{n} \dot{=} t_{n}. A solution, or unifier of S, is a substitution \sigma such that \sigma (s_{i}) = \sigma (t_{i}) for i = 1, \ldots, n. A most general unifier, for short MGU, is a most general such substitution.*

A substitution is idempotent* when \sigma = \sigma \circ \sigma. If \sigma = \lbrace x_{1} \mapsto t_{1}, \ldots, x_{k} \mapsto t_{k} \rbrace, then \sigma is idempotent exactly when no t_{i} contains any of the variables \lbrace x_{1}, \ldots, x_{n} \rbrace; i.e. \lbrace x_{1}, \ldots, x_{n} \rbrace \cap \operatorname{Vars} (t_{1}, \ldots, t_{n}) = \varnothing.*

1. Implement an algorithm that, given a set of equations represented as a list of pairs of terms, computes an idempotent most general unifier of the equations.
2. ** (Ex. 4.22 in* *Franz Baader and Tobias Nipkov “Term Rewriting and All That”**, p. 82.) Modify the implementation of unification to achieve linear space complexity by working with what could be called iterated substitutions. For example, the solution to* \lbrace x =^? f (y), y =^? g (z), z =^? a \rbrace should be represented as variable, term pairs (x, f (y)), (y, g (z)), (z, a). (Hint: iterated substitutions should be unfolded lazily, i.e. only so far that either a non-variable term or the end of the instantiation chain is found.)

Exercise 3:

1. What does it mean that an implementation has junk (as an algebraic structure for a given signature)? Is it bad?
2. Define a monomorphic algebraic specification (other than, but similar to, \operatorname{nat}_{p} or \operatorname{string}_{p}, some useful data type).
3. Discuss an example of a (monomorphic) algebraic specification where it would be useful to drop some axioms (giving up monomorphicity) to allow more efficient implementations.

Exercise 4:

1. Does the example ListMap meet the requirements of the algebraic specification for maps? Hint: here is the definition of List.removeassoc;*compare a x* equals 0 if and only if *a*=*x*.

   let rec removeassoc x = function | [] -> [] | (a, b as pair) :: l -> if compare a x = 0 then l else pair :: removeassoc x l

2. Trick question: what is the computational complexity of ListMap or TrivialMap?

3. ** The implementation* MyListMap is inefficient: it performs a lot of copying and is not tail-recursive. Optimize it (without changing the type definition).

4. Add (and specify) \operatorname{isEmpty}: (\alpha, \beta) \operatorname{map} \rightarrow \operatorname{bool} to the example algebraic specification of maps without increasing the burden on its implementations (i.e. without affecting implementations of other operations). Hint: equational reasoning might be not enough; consider an equivalence relation \approx meaning “have the same keys”, defined and used just in the axioms of the specification.

Exercise 5: Design an algebraic specification and write a signature for first-in-first-out queues. Provide two implementations: one straightforward using a list, and another one using two lists: one for freshly added elements providing efficient queueing of new elements, and “reversed” one for efficient popping of old elements.

Exercise 6: Design an algebraic specification and write a signature for sets. Provide two implementations: one straightforward using a list, and another one using a map into the unit type.

• To allow for a more complete specification of sets here, augment the maps ADT with generally useful operations that you find necessary or convenient for map-based implementation of sets.

Exercise 7:

1. (Ex. 2.2 in *Chris Okasaki “Purely Functional Data Structures”**) In the worst case,* *member* performs approximately 2 d comparisons, where d is the depth of the tree. Rewrite *member* to take no mare than d + 1 comparisons by keeping track of a candidate element that might be equal to the query element (say, the last element for which < returned false) and checking for equality only when you hit the bottom of the tree.
2. (Ex. 3.10 in *Chris Okasaki “Purely Functional Data Structures”**) The *balance* function currently performs several unnecessary tests: when e.g.* *ins* recurses on the left child, there are no violations on the right child.
   1. Split *balance* into *lbalance* and *rbalance* that test for violations of left resp. right child only. Replace calls to *balance* appropriately.
   2. One of the remaining tests on grandchildren is also unnecessary. Rewrite *ins* so that it never tests the color of nodes not on the search path.

Lecture 6: Folding and Backtracking

Mapping and folding.Backtracking using lists. Constraint solving.

Martin Odersky ‘‘Functional Programming Fundamentals’’ Lectures 2, 5 and 6

Bits of Ralf Laemmel ‘‘Going Bananas’’

Graham Hutton ‘‘Programming in Haskell’’ Chapter 11 ‘‘Countdown Problem’’

Tomasz Wierzbicki ‘‘Honey Islands Puzzle Solver’’

If you see any error on the slides, let me know!

1 Plan

• map and fold_right: recursive function examples, abstracting over gets the higher-order functions.
• Reversing list example, tail-recursive variant, fold_left.
• Trimming a list: filter.
  • Another definition via fold_right.
• map and fold for trees and other data structures.
• The point-free programming style. A bit of history: the FP language.
• Sum over an interval example: \sum_{n = a}^b f (n).
• Combining multiple results: concat_map.
• Interlude: generating all subsets of a set (as list), and as exercise: all permutations of a list.
• The Google problem: the map_reduce higher-order function.
  • Homework reference: modified map_reduce to
    1. build a histogram of a list of documents
    2. build an inverted index for a list of documents
    Later: use fold (?) to search for a set of words (conjunctive query).
• Puzzles: checking correctness of a solution.
• Combining bags of intermediate results: the concat_fold functions.
• From checking to generating solutions.
• Improving “generate-and-test” by filtering (propagating constraints) along the way.
• Constraint variables, splitting and constraint propagation.
• Another example with “heavier” constraint propagation.

2 Basic generic list operations

How to print a comma-separated list of integers? In module String:

val concat : string -> string list -> string

First convert numbers into strings:

let rec stringsofints = function | [] -> [] | hd::tl -> stringofint hd :: stringsofints tllet commasepints = String.concat “,” -| stringsofints

How to get strings sorted from shortest to longest? First find the length:

let rec stringslengths = function | [] -> [] | hd::tl -> (String.length hd, hd) :: stringslengths tllet bysize = List.sort compare -| stringslengths

2.1 Always extract common patterns

1.589482.889124.91267032676283.016123164439747.15635335361822.783288133350976.098012303214712.127116682100812.139816774705652.127116682100811.483645323455482.296451250165373.70616-0.561076.6695164704326-0.4552354808837159.37886955946554-0.6034032279402048.15119394099749-1.323075142214584.36233298055298-1.19607421616616-8.062594.51897-5.437905146183364.62480156105305-2.538050668077794.56130109802884-3.5117244344493.79929554173833-7.575754067998413.92629646778674-7.914421.15344-4.506565021828281.30161066278608-2.453383384045510.984108347665035-3.659892181505490.391437359439079-7.575754067998410.4549378224632891.483652.27528-0.506035851303082-3.630258632094194.34117-1.217240.255969704987432-3.63025863209419-7.639253.88396-7.66042135203069-2.1485811615293-3.659890.370271-6.55974665961106-2.12741434052123-8.16843-2.31792-5.94590885037703-2.21208162455351-4.16789588569917-2.27558208757772-4.76056687392512-2.88941989681175-7.78742227807911-2.86825307580368-2.72855-3.79959-0.506035851303082-3.630258632094190.742806588173039-4.053595052255590.213636062971293-4.60393239846541-2.79205252017463-4.41343100939278-5.840072.78329-2.919053446223053.01612316443974-1.05637319751292.78328813335097-1.691377827754992.14828350310888-5.395571504167222.23295078714116-5.33207-0.476402-0.992872734488689-0.2647340918110861.75881399656039-0.5399027649159940.785140230189178-1.21724103717423-4.52773184283635-1.19607421616616-5.459072.19062-5.62840653525599-3.71492591612647-4.52773-1.23841-5.45907196719143-3.778426379150680cm

Now use the generic function:

let commasepints = String.concat “,” -| listmap stringofintlet bysize =
List.sort compare -| listmap (fun s->String.length s, s)

-6.968285.20805-5.592439476121185.48321537240376-4.237762931604715.22921352030692-4.576432067733834.72120981611324-6.354445032411694.70004299510517-6.693111.18635-4.682266172774181.24985117078979-2.756085461039821.1016834237333-3.306422807249640.509012435507342-6.354445032411690.466678793491203-2.269253.7687-0.8722383913216043.7687028707501-0.1102328350310893.45120055562905-0.5759028972086263.04903095647572-2.692584998015613.11253141949993-2.37508-0.549329-0.512402434184416-0.3799940468315911.73128059267099-0.591662256912291.05394232041275-1.16316642413018-2.03641354676544-1.12083278211404-6.92595-2.36968-4.02609472152401-2.11567336949332-0.999239317370023-2.34850840058209-1.48607620055563-2.87767892578383-6.07927635930679-2.87767892578383-2.26925-3.914851.49844556158222-3.809019050138913.40345945230851-4.063020902235752.93778939013097-4.52869096441328-1.27440799047493-4.61335824844556-6.354454.70004-6.10044318031486-2.2003406535256-3.306420.509012-5.10853954194466-2.14605530848409-2.734923.11253-1.38460084405009-3.806950349498371.05394-1.184330.19997872622222-3.78626681481166-3.560423.4512-3.200588702209293.133698240508-3.073587776160873.64170194470168-3.58159-0.760997-2.90425320809631-0.54932861489615-2.75608546103982-0.866830930017198-4.70343-4.21119-4.08959518454822-4.10535454425189-4.1742624685805-4.48635732239714-3.242923.11253-4.3859306786612-3.87251951316312-3.26132-1.28056-4.23776293160471-3.95718679719540cm

2.2 Can we make fold tail-recursive?

Let’s investigate some tail-recursive functions. (Not hidden as helpers.)

-5.909944.94728-3.729759227411035.01078184945099-1.486076200555634.88378092340257-2.099914009789654.33344357719275-5.338437624024344.26994311416854-5.867611.47592-2.756085461039821.666424130175950.7152731842836351.49708956211139-0.4489019711602060.925585394893504-4.936268024871010.925585394893504-6.01578-2.79978-2.69258499801561-2.56694007143802-0.152566477047228-2.79977510252679-0.427735150152137-3.30777880672047-4.57643206773383-3.35011244873661-3.750933.06343-2.121080830797723.29626934779733-0.5970697182166953.04226749570049-2.226914935838072.55543061251488-4.02609-1.1911-2.45974996692684-0.852427569784363-1.21090752745072-1.25459716893769-2.43858314591877-1.63559994708295-4.5341-4.40845-2.37508268289456-4.28145257309168-0.343067866119857-4.4084534991401-1.02040613837809-4.93762402434184-3.83559333245138-4.93762402434184-0.1102333.296271.498445561582223.423270273845752.874288927106763.232768884773122.175783833840452.555430612514880.1437690170657492.57659743352295-0.491236-0.9582623.61512766238921-0.8100939277682237.04415266569652-1.064095779865065.71064294218812-1.720267231115230.524771795211007-1.677933589099090.376604-4.302622.21811747585659-4.239118931075543.61512766238921-4.429620320148173.17062442121974-4.916457203333770.799940468315915-4.95879084534991-5.338444.29111-6.07927635930679-2.16477047228469-5.69827358116153-2.69394099748644-4.957430.967919-5.48660537108083-1.97426908321207-5.44427172906469-2.6516073554703-2.226912.55543-2.03641354676544-3.62528112184151-2.37508268289456-4.28145257309168-2.41742-1.61443-2.69258499801561-3.79461568990607-2.80072853017803-4.283284085867292.895463.253945.64714247916391-2.397605503373463.72096176742955-4.429620320148174.73754-1.786764.14429818759095-3.413612911760813.50929355734886-4.323786215107820.5036052.70363.00128985315518-4.49312078317238-0.0678992-1.50862.89545574811483-4.598954888212731.752452.70361.62544648763064-4.450787141156242.47212-1.57213.04362349517132-2.461105966397676.17631-1.50863.04362349517132-2.461105966397673.04362-2.461112.02761608678397-4.366119857123960cm

• With fold_left, it is easier to hide the accumulator. The average example is a bit more tricky than list_rev.

  let listrev l = foldleft (fun t h->h::t) [] llet average = foldleft (fun (sum,tot) e->sum +. e, 1. +. tot) (0.,0.)

• The function names and order of arguments for List.fold_right / List.fold_left are due to:

  • fold_right f makes f right associative, like list constructor ::

    List.foldright f [a1; …; an] b is f a1 (f a2 (… (f an b) …)).

  • fold_left f makes f left associative, like function application

    List.foldleft f a [b1; …; bn] is f (… (f (f a b1) b2) …) bn.

• The “backward” structure of fold_left computation:

• List filtering, already rather generic (a polymorphic higher-order function)

  let listfilter p l = List.foldright (fun h t->if p h then h::t else t) l []

• Tail-recursive map returning elements in reverse order:

  let listrevmap f l = List.foldleft (fun t h->f h::t) [] l

3 map and fold for trees and other structures

• Mapping binary trees is straightforward:

  type ’a btree = Empty | Node of ’a * ’a btree * ’a btree let rec btmap f = function | Empty -> Empty | Node (e, l, r) -> Node (f e, btmap f l, btmap f r) let test = Node (3, Node (5, Empty, Empty), Node (7, Empty, Empty))let = btmap ((+) 1) test

• map and fold we consider in this section preserve / respect the structure of the data, they do not correspond to map and fold of abstract data type containers, which are like List.rev_map and List.fold_left over container elements listed in arbitrary order.

  • I.e. here we generalize List.map and List.fold_right to other structures.

• fold in most general form needs to process the element together with partial results for the subtrees.

  let rec btfold f base = function | Empty -> base | Node (e, l,

  18. -> f e (btfold f base l) (btfold f base r)

• Examples:

  let sumels = btfold (fun i l r -> i + l + r) 0let depth t = btfold (fun
  l r -> 1 + max l r) 1 t

3.1 map and fold for more complex structures

To have a data structure to work with, we recall expressions from lecture 3.

type expression = Const of float | Var of string | Sum of expression * expression (* e1 + e2 ) | Diff of expression expression (* e1 - e2 ) | Prod of expression expression (* e1 * e2 ) | Quot of expression expression (* e1 / e2 *)

Multitude of cases make the datatype harder to work with. Fortunately, or-patterns help a bit:

let rec vars = function | Const -> [] | Var x -> [x] | Sum (a,b) | Diff (a,b) | Prod (a,b) | Quot (a,b) -> vars a @ vars b

Mapping and folding needs to be specialized for each case. We pack the behaviors into a record.

type expressionmap = { mapconst : float -> expression; mapvar : string -> expression; mapsum : expression -> expression -> expression; mapdiff : expression -> expression -> expression;
mapprod : expression -> expression -> expression; mapquot : expression -> expression -> expression;}Note how expression from above is substituted by 'a below, explain why?type ’a expressionfold = {
foldconst : float -> ’a; foldvar : string -> ’a; foldsum : ’a -> ’a -> ’a; folddiff : ’a -> ’a -> ’a; foldprod : ’a -> ’a -> ’a; foldquot : ’a -> ’a -> ’a;}

Next we define standard behaviors for map and fold, which can be tailored to needs for particular case.

let identitymap = { mapconst = (fun c -> Const c); mapvar = (fun x -> Var x); mapsum = (fun a b -> Sum (a, b)); mapdiff = (fun a b -> Diff (a, b)); mapprod = (fun a b -> Prod (a, b)); mapquot = (fun a b -> Quot (a, b));}let makefold op base = { foldconst = (fun -> base); foldvar = (fun -> base); foldsum = op; folddiff = op;
foldprod = op; foldquot = op;}

The actual map and fold functions are straightforward:

let rec exprmap emap = function | Const c -> emap.mapconst c | Var x -> emap.mapvar x | Sum (a,b) -> emap.mapsum (exprmap emap a) (exprmap emap b) | Diff (a,b) -> emap.mapdiff (exprmap emap a) (exprmap emap b) | Prod (a,b) -> emap.mapprod (exprmap emap a) (exprmap emap b) | Quot (a,b) -> emap.mapquot (exprmap emap a) (exprmap emap b)let rec exprfold efold = function | Const c -> efold.foldconst c | Var x -> efold.foldvar x | Sum (a,b) -> efold.foldsum (exprfold efold a) (exprfold efold b) | Diff (a,b) -> efold.folddiff (exprfold efold a) (exprfold efold b) | Prod (a,b) -> efold.foldprod (exprfold efold a) (exprfold efold b) | Quot (a,b) -> efold.foldquot (exprfold efold a) (exprfold efold b)

Now examples. We use {record with field=value} syntax which copies record but puts value instead of record.field in the result.

let primevars = exprmap {identitymap with mapvar = fun x -> Var (x”’“)}let subst s = let apply x = try List.assoc x s with Notfound -> Var x in exprmap {identitymap with mapvar = apply}let vars = exprfold {(makefold (@) []) with foldvar = fun x-> [x]}let size = exprfold (makefold (fun a b->1+a+b) 1)let eval env = exprfold { foldconst = id;
foldvar = (fun x -> List.assoc x env); foldsum = (+.); folddiff = (-.);
foldprod = ( *.); foldquot = (/.);}

4 Point-free Programming

• In 1977/78, John Backus designed FP, the first function-level programming language. Over the next decade it evolved into the FL language.

  • ”Clarity is achieved when programs are written at the function level –that is, by putting together existing programs to form new ones, rather than by manipulating objects and then abstracting from those objects to produce programs.” The FL Project: The Design of a Functional Language

• For functionl-level programming style, we need functionals/combinators, like these from OCaml Batteries: let const x = xlet ( |- ) f g x = g (f x)let ( -| ) f g x = f (g x)let flip f x y = f y xlet ( *** ) f g = fun (x,y) -> (f x, g y)let ( &&& ) f g = fun x -> (f x, g x)let first f x = fst (f x)let second f x = snd (f x)let curry f x y = f (x,y)let uncurry f (x,y) = f x y

• The flow of computation can be seen as a circuit where the results of nodes-functions are connected to further nodes as inputs.

  We can represent the cross-sections of the circuit as tuples of intermediate values.

• let print2 c i = let a = Char.escaped c in let b = stringofint i in a b

-9.51-4.01.0-9.4935-0.00601931-4.00.0Char.escaped-41string_of_int-4.05-5.47857e-050.513.50.50.5395720333377430.0151475062839uncurry (^)3.50.57.50.510.50.50cm

• Since we usually work by passing arguments one at a time rather than in tuples, we need uncurry to access multi-argument functions, and we pack the result with curry.

  • Turning C/Pascal-like function into one that takes arguments one at a time is called currification, after the logician Haskell Brooks Curry.

• Another option to remove explicit use of function parameters, rather than to pack intermediate values as tuples, is to use function composition, flip, and the so called S combinator:

  let s x y z = x z (y z)

  to bring a particular argument of a function to “front”, and pass it a result of another function. Example: a filter-map function

  let func2 f g l = List.filter f (List.map g (l))Definition of function composition.let func2 f g = (-|) (List.filter f) (List.map g)let func2 f = (-|) (List.filter f) -| List.mapCompositionagain, below without the infix notation.let func2 f = (-|) ((-|) (List.filter f)) List.maplet func2 f = flip (-|) List.map ((-|) (List.filter f))let func2 f = (((|-) List.map) -| ((-|) -| List.filter)) flet func2 = (|-) List.map -| ((-|) -| List.filter)

5 Reductions. More higher-order/list functions

Mathematics has notation for sum over an interval: \sum_{n = a}^b f (n).

In OCaml, we do not have a universal addition operator:

let rec isumfromto f a b = if a > b then 0 else f a + isumfromto f (a+1) blet rec fsumfromto f a b = if a > b then 0. else f a +. fsumfromto f (a+1) blet pi2over6 = fsumfromto (fun i->1. /. floatofint (i*i)) 1 5000

It is natural to generalize:

let rec opfromto op base f a b = if a > b then base else op (f a) (opfromto op base f (a+1) b)

Let’s collect the results of a multifunction (i.e. a set-valued function) for a set of arguments, in math notation:

f (A) = \bigcup_{p \in A} f (p)

It is a useful operation over lists with union translated as append:

let rec concatmap f = function | [] -> [] | a::l -> f a @ concatmap f l

and more efficiently:

let concatmap f l = let rec cmapf accu = function | [] -> accu | a::l -> cmapf (List.revappend (f a) accu) l in List.rev (cmapf [] l)

5.1 List manipulation: All subsequences of a list

let rec subseqs l = match l with | [] -> [[]] | x::xs ->
let pxs = subseqs xs in List.map (fun px -> x::px) pxs @ pxs

Tail-recursively:

let rec rmapappend f accu = function | [] -> accu | a::l -> rmapappend f (f a :: accu) l

let rec subseqs l = match l with | [] -> [[]] | x::xs ->
let pxs = subseqs xs in rmapappend (fun px -> x::px) pxs pxs

In-class work: Return a list of all possible ways of splitting a list into two non-empty parts.

Homework:

Find all permutations of a list.

Find all ways of choosing without repetition from a list.

5.2 By key: group_by and map_reduce

It is often useful to organize values by some property.

First we collect an elements from an association list by key.

let collect l = match List.sort (fun x y -> compare (fst x) (fst y)) l with | [] -> []Start with associations sorted by key. | (k0, v0)::tl -> let k0, vs, l = List.foldleft (fun (k0, vs, l) (kn, vn) ->Collect values for the current key if k0 = kn then k0, vn::vs, land when the key changes else kn, [vn], (k0,List.rev vs)::l)stack the collected values. (k0, [v0], []) tl inWhat do we gain by reversing?
List.rev ((k0,List.rev vs)::l)

Now we can group by an arbitrary property:

let groupby p l = collect (List.map (fun e->p e, e) l)

But we want to process the results, like with an aggregate operation in SQL. The aggregation operation is called reduction.

let aggregateby p red base l = let ags = groupby p l in List.map (fun (k,vs)->k, List.foldright red vs base) ags

We can use the feed-forward operator: let ( |> ) x f = f x

let aggregateby p redf base l = groupby p l |> List.map (fun (k,vs)->k, List.foldright redf vs base)

Often it is easier to extract the property over which we aggregate upfront. Since we first map the elements into the extracted key-value pairs, we call the operation map_reduce:

let mapreduce mapf redf base l = List.map mapf l |> collect |> List.map (fun (k,vs)->k, List.foldright redf vs base)

5.2.1 map_reduce/concat_reduce examples

Sometimes we have multiple sources of information rather than records.

let concatreduce mapf redf base l = concatmap mapf l |> collect |> List.map (fun (k,vs)->k, List.foldright redf vs base)

Compute the merged histogram of several documents:

let histogram documents = let mapf doc = Str.split (Str.regexp “[ t.,;]+”) doc |> List.map (fun word->word,1) in concatreduce mapf (+) 0 documents

Now compute the inverted index of several documents (which come with identifiers or addresses).

let cons hd tl = hd::tllet invertedindex documents = let mapf (addr, doc) =
Str.split (Str.regexp “[ t.,;]+”) doc |> List.map (fun word->word,addr) in concatreduce mapf cons [] documents

And now… a “search engine”:

let search index words = match List.map (flip List.assoc index) words with | [] -> [] | idx::idcs -> List.foldleft intersect idx idcs

where intersect computes intersection of sets represented as lists.

5.2.2 Tail-recursive variants

let revcollect l = match List.sort (fun x y -> compare (fst x) (fst y)) l with | [] -> [] | (k0, v0)::tl -> let k0, vs, l = List.foldleft
(fun (k0, vs, l) (kn, vn) -> if k0 = kn then k0, vn::vs, l
else kn, [vn], (k0, vs)::l) (k0, [v0], []) tl in List.rev ((k0, vs)::l)

let trconcatreduce mapf redf base l = concatmap mapf l |> revcollect
|> List.revmap (fun (k,vs)->k, List.foldleft redf base vs)

let rcons tl hd = hd::tllet invertedindex documents = let mapf (addr, doc) = … in trconcatreduce mapf rcons [] documents

5.2.3 Helper functions for inverted index demonstration

let intersect xs ys =Sets as sorted lists. let rec aux acc = function
| [], | , [] -> acc | (x::xs’ as xs), (y::ys’ as ys) -> let c = compare x y in if c = 0 then aux (x::acc) (xs’, ys’) else if c < 0 then aux acc (xs’, ys) else aux acc (xs, ys’) in List.rev (aux [] (xs, ys))

let readlines file = let input = openin file in let rec read lines =The Scanf library uses continuation passing. try Scanf.fscanf input “%[]” (fun x -> read (x :: lines)) with Endoffile -> lines in
List.rev (read [])

let indexed l =Index elements by their positions. Array.oflist l |> Array.mapi (fun i e->i,e) |> Array.tolist

let searchengine lines = let lines = indexed lines in let index = invertedindex lines in fun words -> let ans = search index words in
List.map (flip List.assoc lines) ans

let searchbible = searchengine (readlines “./bible-kjv.txt”)let testresult =
searchbible [“Abraham”; “sons”; “wife”]

5.3 Higher-order functions for the option type

Operate on an optional value:

let mapoption f = function | None -> None | Some e -> f e

Map an operation over a list and filter-out cases when it does not succeed:

let rec mapsome f = function | [] -> [] | e::l -> match f e with
| None -> mapsome f l | Some r -> r :: mapsome f lTail-recurively:

let mapsome f l = let rec mapsf accu = function | [] -> accu | a::l -> mapsf (match f a with None -> accu | Some r -> r::accu) l in List.rev (mapsf [] l)

6 The Countdown Problem Puzzle

• Using a given set of numbers and arithmetic operators +, -, *, /, construct an expression with a given value.

• All numbers, including intermediate results, must be positive integers.

• Each of the source numbers can be used at most once when constructing the expression.

• Example:

  • numbers 1, 3, 7, 10, 25, 50
  • target 765
  • possible solution (25-10) * (50+1)

• There are 780 solutions for this example.

• Changing the target to 831 gives an example that has no solutions.

• Operators:

  type op = Add | Sub | Mul | Div

• Apply an operator:

  let apply op x y = match op with | Add -> x + y | Sub -> x - y | Mul -> x * y | Div -> x / y

• Decide if the result of applying an operator to two positive integers is another positive integer:

  let valid op x y = match op with | Add -> true | Sub -> x > y | Mul -> true | Div -> x mod y = 0

• Expressions:

  type expr = Val of int | App of op * expr * expr

• Return the overall value of an expression, provided that it is a positive integer:

  let rec eval = function | Val n -> if n > 0 then Some n else None
  | App (o,l,r) -> eval l |> mapoption (fun x -> eval r |> mapoption (fun y -> if valid o x y then Some (apply o x y)
  else None))

• Homework: Return a list of all possible ways of choosing zero or more elements from a list – choices.

• Return a list of all the values in an expression:

  let rec values = function | Val n -> [n] | App (,l,r) -> values l @ values r

• Decide if an expression is a solution for a given list of source numbers and a target number:

  let solution e ns n = listdiff (values e) ns = [] && isunique (values e) && eval e = Some n

6.1 Brute force solution

• Return a list of all possible ways of splitting a list into two non-empty parts:

  let split l = let rec aux lhs acc = function | [] | [] -> [] | [y; z] -> (List.rev (y::lhs), [z])::acc | hd::rhs -> let lhs = hd::lhs in aux lhs ((List.rev lhs, rhs)::acc) rhs in aux [] [] l

• We introduce an operator to work on multiple sources of data, producing even more data for the next stage of computation:

  let ( |-> ) x f = concatmap f x

• Return a list of all possible expressions whose values are precisely a given list of numbers:

  let combine l r =Combine two expressions using each operator. List.map (fun o->App (o,l,r)) [Add; Sub; Mul; Div]let rec exprs = function | [] -> [] | [n] -> [Val n] | ns -> split ns |-> (fun (ls,rs) ->For each split ls,rs of numbers, exprs ls |-> (fun l ->for each expression l over ls exprs rs |-> (fun r ->and expression r over rs combine l r)))produce all l ? r expressions.

• Return a list of all possible expressions that solve an instance of the countdown problem:

  let guard n = List.filter (fun e -> eval e = Some n)

  let solutions ns n = choices ns |-> (fun ns’ -> exprs ns’ |> guard n)

• Another way to express this:

  let guard p e = if p e then [e] else []

  let solutions ns n = choices ns |-> (fun ns’ -> exprs ns’ |-> guard (fun e -> eval e = Some n))

6.2 Fuse the generate phase with the test phase

• We seek to define a function that fuses together the generation and evaluation of expressions:

  • We memorize the value together with the expression – in pairs (e, eval e) – so only valid subexpressions are ever generated.

  let combine’ (l,x) (r,y) = [Add; Sub; Mul; Div] |> List.filter (fun o->valid o x y) |> List.map (fun o->App (o,l,r), apply o x y)let rec results = function | [] -> [] | [n] -> if n > 0 then [Val n, n] else [] | ns -> split ns |-> (fun (ls,rs) ->
  results ls |-> (fun lx -> results rs |-> (fun ry ->
  combine’ lx ry)))

• Once the result is generated its value is already computed, we only check if it equals the target.

  let solutions’ ns n = choices ns |-> (fun ns’ -> results ns’ |> List.filter (fun (e,m)-> m=n) |> List.map fst)We discard the memorized values.

6.3 Eliminate symmetric cases

• Strengthening the valid predicate to take account of commutativity and identity properties:

  let valid op x y = match op with | Add -> x <= y | Sub -> x > y | Mul -> x <= y && x <> 1 && y <> 1 | Div -> x mod y = 0 && y <> 1

  • We eliminate repeating symmetrical solutions on the semantic level, i.e.  on values, rather than on the syntactic level of expressions – it is both easier and gives better results.

• Now recompile combine’, results and solutions’.

7 The Honey Islands Puzzle

• Be a bee! Find the cells to eat honey out of, so that the least amount of honey becomes sour, assuming that sourness spreads through contact.
  • Honey sourness is totally made up, sorry.
• Each honeycomb cell is connected with 6 other cells, unless it is a border cell. Given a honeycomb with some cells initially marked as black, mark some more cells so that unmarked cells form num_islands disconnected components, each with island_size cells.

Task: 3 islands x 3Solution:

7.1 Representing the honeycomb

type cell = int * intWe address cells using ‘‘cartesian’’ coordinatesmodule CellSet =and store them in either lists or sets. Set.Make (struct type t = cell let compare = compare end)type task = {For board ‘‘size’’ N, the honeycomb coordinates boardsize : int;range from (- 2 N, - N) to 2 N, N.
numislands : int;Required number of islands islandsize : int;and required number of cells in an island. emptycells : CellSet.t;The cells that are initially without honey.}

let cellsetoflist l =List into set, inverse of CellSet.elements
List.foldright CellSet.add l CellSet.empty

7.1.1 Neighborhood

x,y-0.902203-0.291672x+2,y2.23049-0.376339x+1,y+10.410142.35418x-1,y+1-2.637882.33301x-2,y-4.20423-0.418673x-1,y-1-2.65905-3.08569x+1,y-10.431307-3.191530cm

let neighbors n eaten (x,y) = List.filter (insideboard n eaten) [x-1,y-1; x+1,y-1; x+2,y; x+1,y+1; x-1,y+1; x-2,y]

7.1.2 Building the honeycomb

0,0-0.373032-0.1543520,2-0.3730323.041840,-2-0.394199-3.541041,10.5159741.496664,03.33116-0.239023,12.505661.496662,21.510813.063-2,0-2.23571-0.1543520cm

let even x = x mod 2 = 0

let insideboard n eaten (x, y) = even x = even y && abs y <= n && abs x + abs y <= 2*n && not (CellSet.mem (x,y) eaten)

let honeycells n eaten = fromto (-2n) (2n)|->(fun x -> fromto (-n) n |-> (fun y -> guard (insideboard n eaten) (x, y)))

7.1.3 Drawing honeycombs

We separately generate colored polygons:

let drawhoneycomb \simw \simh task eaten = let i2f = floatofint in let nx = i2f (4 * task.boardsize + 2) in let ny = i2f (2 * task.boardsize + 2) in let radius = min (i2f w /. nx) (i2f h /. ny) in let x0 = w / 2 in let y0 = h / 2 in let dx = (sqrt 3. /. 2.) . radius +. 1. inThe distance between let dy = (3. /. 2.) . radius +. 2. in(x, y) and (x + 1, y + 1). let drawcell (x,y) = Array.init 7We draw a closed polygon by placing 6 points (fun i ->evenly spaced on a circumcircle. let phi = floatofint i . pi /. 3. in x0 + intoffloat (radius . sin phi +. floatofint x . dx), y0 + intoffloat (radius . cos phi +. floatofint y *. dy)) in let honey = honeycells task.boardsize (CellSet.union task.emptycells (cellsetoflist eaten)) |> List.map (fun p->drawcell p, (255, 255, 0)) in let eaten = List.map (fun p->drawcell p, (50, 0, 50)) eaten in let oldempty = List.map (fun p->drawcell p, (0, 0, 0)) (CellSet.elements task.emptycells) in honey @ eaten @ oldempty

We can draw the polygons to an SVG image:

n” title); (match desc with None -> () | Some desc -> Printf.fprintf f ” %sn” desc); let drawshape (points, (r,g,b)) = uncurry (Printf.fprintf f ” <path d=“M %d %d”) points.(0); Array.iteri (fun i (x, y) -> if i > 0 then Printf.fprintf f ” L %d %d” x y) points; Printf.fprintf f ““n fill=”rgb(%d, %d, %d)” stroke-width=“3” />n” r g b in List.iter drawshape curves; Printf.fprintf f “%!”

But we also want to draw on a screen window – we need to link the Graphics library. In the interactive toplevel:

##load “graphics.cma”;;

When compiling we just provide graphics.cma to the command.

let drawtoscreen \simw \simh curves = Graphics.opengraph (” “stringofint w”x”stringofint h); Graphics.setcolor (Graphics.rgb 50 50 0);We draw a brown background. Graphics.fillrect 0 0 (Graphics.sizex ()) (Graphics.sizey ()); List.iter (fun (points, (r,g,b)) -> Graphics.setcolor (Graphics.rgb r g b); Graphics.fillpoly points) curves; if Graphics.readkey () = 'q'We wait so that solutions can be seen then failwith “User interrupted finding solutions.”;as they’re computed. Graphics.closegraph ()

7.2 Testing correctness of a solution

We walk through each island counting its cells, depth-first: having visited everything possible in one direction, we check whether something remains in another direction.

Correctness means there are numislands components each with islandsize cells. We start by computing the cells to walk on: honey.

let checkcorrect n islandsize numislands emptycells = let honey = honeycells n emptycells in

We keep track of already visited cells and islands. When an unvisited cell is there after walking around an island, it must belong to a different island.

let rec checkboard beenislands unvisited visited = match unvisited with
| [] -> beenislands = numislands | cell::remaining when CellSet.mem cell visited -> checkboard been_islands remaining visitedKeep looking.
| cell::remaining (* when not visited *) -> let (beensize, unvisited, visited) = checkisland cellVisit another island.(1, remaining, CellSet.add cell visited) in beensize = islandsize && checkboard (beenislands+1) unvisited visited

When walking over an island, besides the unvisited and visited cells, we need to remember been_size – number of cells in the island visited so far.

and checkisland current state = neighbors n emptycells current |> List.foldleft Walk into each direction and accumulate visits.(fun (beensize, unvisited, visited as state) neighbor -> if CellSet.mem neighbor visited then state else let unvisited = remove neighbor unvisited in let visited = CellSet.add neighbor visited in
let beensize = beensize + 1 in checkisland neighbor
(beensize, unvisited, visited)) state inStart from the current overall state (initial been_size is 1).

Initially there are no islands already visited.

checkboard 0 honey emptycells

7.3 Interlude: multiple results per step

When there is only one possible result per step, we work through a list using List.foldright and List.foldleft functions.

What if there are multiple results? Recall that when we have multiple sources of data and want to collect multiple results, we use concat_map:

-4.568261.32331-3.509921.34447-2.218751.32331-0.9699031.323310.3424391.30214-4.568261.32331-5.541936764122240.264965603915862-4.568261.32331-4.695263923799440.328466066940071-4.568261.32331-4.039092472549280.286132424923932-3.509921.34447-3.573422410371740.391966529964281-3.509921.34447-2.896084138113510.370799708956211-2.218751.32331-2.451580896944040.434300171980421-0.9699031.32331-1.604908056621250.413133350972351-0.9699031.32331-0.8640693213388010.3919665299642811.316111.386811.316111.386810.405939939145390.4554669929884911.316111.386811.083278211403620.476633813996561.316111.386811.8029501256780.4131333509723511.316111.386812.586122502976580.54013427702077-5.541940.264966-5.541940.264966-4.695260.328466-4.039090.286132-3.573420.391967-2.896080.3708-2.451580.4343-1.604910.413133-0.8640690.3919670.405940.4554671.083280.4766341.802950.4131332.586120.540134-5.774770.624802-6.007606826299780.56130109802884-6.02877364730784-0.0525367112051859-5.73243815319487-0.116037174229395-4.017930.794136-3.890924725492790.56130109802884-3.933258367508930.0109637518190237-4.22959386162191-0.116037174229395-3.763920.878803-3.679256515412090.0532973938351634-3.44642148432332-0.031369890197116-2.874920.89997-2.769083212065090.688302024077259-2.76908321206509-0.0102030691890462-2.98075142214579-0.031369890197116-2.557420.89997-2.557415001984390.0956310358513031-2.45158089694404-0.0737035322132557-2.091740.815303-2.007077655774570.688302024077259-2.070578118798780.0744642148432332-2.23991268686334-0.031369890197116-1.668410.878803-1.816576266701940.794136129117608-1.837743087710010.0532973938351634-1.62607487762932-0.137203995237465-0.6312340.878803-0.4830665431935440.794136129117608-0.5254001852096840.0956310358513031-0.821735679322662-0.0948703532213256-0.01739650.857637-0.1443974070644270.794136129117608-0.2078978700886360.264965603915862-0.1443974070644270.1379646778674430.1731050.7518020.0672708030162720.1591314988755130.469440.8788030.300105834105040.9634706971821670.278939013096970.05329739383516340.4271067601534590.05329739383516342.649620.9423042.882457997089560.8999702341579572.84012435507342-0.0313698901971162.48028839793623-0.0525367112051859-5.541940.264966-5.54193676412224-0.539373594390792-4.695260.328466-4.71643074480751-0.560540415398862-3.573420.391967-3.55225558936367-0.539373594390792-2.896080.3708-2.89608413811351-0.539373594390792-1.604910.413133-1.62607487762932-0.560540415398862-0.8640690.391967-0.864069321338801-0.5817072364069320.405940.4554670.38477311813732-0.5605404153988621.083280.4766341.06211139039556-0.4970399523746531.802950.4131331.78178330466993-0.4758731313665832.586120.5401342.5014552189443-0.497039952374653-5.54194-0.539374-4.71643-0.56054-3.55226-0.539374-2.89608-0.539374-1.62607-0.56054-0.864069-0.5817070.384773-0.560541.06211-0.497041.78178-0.4758732.50146-0.49704-5.541941.55614-5.859439079243291.47147440137584-5.859439079243291.11163844423866-5.626604048154520.9846375181902372.120451.534972.416787934912031.492641222383912.416787934912031.196305728270942.205119724831331.13280526524673-5.98644-0.306539-6.28277549940468-0.348872205318164-6.24044185738854-0.687541341447281-5.9229395422675-0.856875909511842.96713-0.2218713.30579441725096-0.3700390263262343.30579441725096-0.6452076994311422.88245799708956-0.85687590951184concat_map-11.06650.984638f xs =-10.34680.264966List.map f xs3.707961.04814|> List.concat3.87730.0744642

We shortened concat_map calls using “work |-> (fun a_result -> …)” scheme. Here we need to collect results once per step.

let rec concatfold f a = function | [] -> [a] | x::xs -> f x a |-> (fun a’ -> concatfold f a’ xs)

7.4 Generating a solution

We turn the code for testing a solution into one that generates a correct solution.

• We pass around the current solution eaten.
• The results will be in a list.
• Empty list means that in a particular case there are no (further) results.
• When walking an island, we pick a new neighbor and try eating from it in one set of possible solutions – which ends walking in its direction, and walking through it in another set of possible solutions.
  • When testing a solution, we never decided to eat from a cell.

The generating function has the same signature as the testing function:

let findtoeat n islandsize numislands emptycells = let honey = honeycells n emptycells in

Since we return lists of solutions, if we are done with current solution eaten we return [eaten], and if we are in a “dead corner” we return [].

let rec findboard beenislands unvisited visited eaten = match unvisited with | [] -> if beenislands = numislands then [eaten] else [] | cell::remaining when CellSet.mem cell visited -> findboard beenislands remaining visited eaten | cell::remaining (* when not visited *) -> findisland cell (1, remaining, CellSet.add cell visited, eaten) |->Concatenate solutions for each way of eating cells around and island. (fun (beensize, unvisited, visited, eaten) ->
if beensize = islandsize then findboard (beenislands+1)
unvisited visited eaten else [])

We step into each neighbor of a current cell of the island, and either eat it or walk further.

and findisland current state = neighbors n emptycells current |> concatfoldInstead of fold_left since multiple results.(fun neighbor
(beensize, unvisited, visited, eaten as state) -> if CellSet.mem neighbor visited then [state] else let unvisited = remove neighbor unvisited in let visited = CellSet.add neighbor visited in (beensize, unvisited, visited,
neighbor::eaten):: (* solutions where neighbor is honey *)
findisland neighbor (beensize+1, unvisited, visited, eaten)) state in

The initial partial solution is – nothing eaten yet.

checkboard 0 honey emptycells []

We can test it now:

let w = 800 and h = 800let ans0 = findtoeat testtask0.boardsize testtask0.islandsize testtask0.numislands testtask0.emptycellslet = drawtoscreen \simw \simh (drawhoneycomb \simw \simh testtask0 (List.hd ans0))

But in a more complex case, finding all solutions takes too long:

let ans1 = findtoeat testtask1.boardsize testtask1.islandsize testtask1.numislands testtask1.emptycellslet = drawtoscreen \simw \simh (drawhoneycomb \simw \simh testtask1 (List.hd ans1))

(See Lec6.ml for definitions of test cases.)

7.5 Optimizations for Honey Islands

• Main rule: fail (drop solution candidates) as early as possible.
  • Is the number of solutions generated by the more brute-force approach above 2^n for n honey cells, or smaller?
• We will guard both choices (eating a cell and keeping it in island).
• We know exactly how much honey needs to be eaten.
• Since the state has many fields, we define a record for it.

type state = { beensize: int;Number of honey cells in current island.
beenislands: int;Number of islands visited so far. unvisited: cell list;Cells that need to be visited. visited: CellSet.t;Already visited. eaten: cell list;Current solution candidate. moretoeat: int;Remaining cells to eat for a complete solution.}

We define the basic operations on the state up-front. If you could keep them inlined, the code would remain more similar to the previous version.

let rec visitcell s = match s.unvisited with | [] -> None | c::remaining when CellSet.mem c s.visited -> visitcell {s with unvisited=remaining} | c::remaining (* when c not visited *) -> Some (c, {s with unvisited=remaining; visited = CellSet.add c s.visited})

let eatcell c s = {s with eaten = c::s.eaten; visited = CellSet.add c s.visited; moretoeat = s.moretoeat - 1}

let keepcell c s =Actually c is not used… {s with beensize = s.beensize + 1; visited = CellSet.add c s.visited}

let freshisland s =We increase been_size at the start of find_island {s with beensize = 0;rather than before calling it. beenislands = s.beenislands + 1}

let initstate unvisited moretoeat = { beensize =5mm 0; beenislands = 0;
unvisited; visited = CellSet.empty; eaten = []; moretoeat;}

We need a state to begin with:

let initstate unvisited moretoeat = { beensize = 0; beenislands = 0;
unvisited; visited = CellSet.empty; eaten = []; moretoeat;}

The “main loop” only changes because of the different handling of state.

let rec findboard s = match visitcell s with | None -> if s.beenislands = numislands then [eaten] else [] | Some (cell, s) ->
findisland cell (freshisland s) |-> (fun s -> if s.beensize = s.islandsize then findboard s else [])

In the “island loop” we only try actions that make sense:

and findisland current s = let s = keepcell current s in neighbors n emptycells current |> concatfold (fun neighbor s ->
if CellSet.mem neighbor s.visited then [s] else let chooseeat =Guard against actions that would fail. if s.moretoeat = 0 then [] else [eatcell neighbor s] and choosekeep = if s.beensize >= islandsize then [] else findisland neighbor s in chooseeat @ choosekeep) s in

Finally, we compute the required length of eaten and start searching.

let cellstoeat = List.length honey - islandsize * numislands in
findboard (initstate honey cellstoeat)

8 Constraint-based puzzles

• Puzzles can be presented by providing the general form of solutions, and additional requirements that the solutions must meet.

• For many puzzles, the general form of solutions for a given problem can be decomposed into a fixed number of variables.

  • A domain of a variable is a set of possible values the variable can have in any solution.
  • In the Honey Islands puzzle, the variables correspond to cells and the domains are \lbrace \operatorname{Honey}, \operatorname{Empty} \rbrace (either a cell has honey, or is empty – without distinguishing “initially empty” and “eaten”).
  • In the Honey Islands puzzle, the constraints are: a selection of cells that have to be empty, the number and size of connected components of cells that are not empty. The neighborhood graph – which cell-variable is connected with which – is part of the constraints.

• There is a general and often efficient scheme of solving constraint-based problems. Finite Domain Constraint Programming algorithm:

  1. With each variable, associate a set of values, initially equal to the domain of the variable. The singleton containing the association is the initial set of partial solutions.
  2. While there is a solution with more than one value associated to some variable in the set of partial solutions, select it and:
     1. If there is a possible value for some variable, such that for all possible assignments of values to other variables, the requirements fail, remove this value from the set associated with this variable.
     2. If there is a variable with empty set of possible values associated to it, remove the solution from the set of partial solutions.
     3. Select the variable with the smallest non-singleton set associated with it (i.e. the smallest greater than 2 size). Split that set into similarly-sized parts. Replace the solution with two solutions where the variable is associated with either of the two parts.
  3. The final solutions are built from partial solutions by assigning to a variable the single possible value associated with it.

• This general algorithm can be simplified. For example, in step (2.c), instead of splitting into two equal-sized parts, we can partition into a singleton and remainder, or partition “all the way” into several singletons.

• The above definition of finite domain constraint solving algorithm is sketchy. Questions?

• We will not discuss a complete implementation example, but you can exploit ideas from the algorithm in your homework.

• Recall how we generated all subsequences of a list. Find (i.e. generate) all:

  1. permutations of a list;
  2. ways of choosing without repetition from a list;
  3. combinations of K distinct objects chosen from the N elements of a list.

• Using folding for the expression data type, compute the degree of the corresponding polynomial. See http://en.wikipedia.org/wiki/Degree_of_a_polynomial.

• Implement simplification of expressions using mapping for the expression data type.

• Express in terms of fold_left or fold_right:

  1. indexed : ’a list -> (int * ’a) list, which pairs elements with their indices in the list;
  2. * concat_fold, as used in the solution of Honey Islands puzzle:
     • let rec concatfold f a = function | [] -> [a] | x::xs ->
       f x a |-> (fun a’ -> concatfold f a’ xs)
     • Hint – consider the function:let rec concatfoldl f a = function | [] -> a | x::xs -> concatfoldl f (concatmap (f x) a) xs
  3. run-length encoding of a list (exercise 10 from 99 Problems).
     • encode [‘a;‘a;‘a;‘a;‘b;‘c;‘c;‘a;‘a;‘d] = [4,‘a; 1,‘b; 2,‘c; 2,‘a; 1,‘d]
• 1. Write a more efficient variant of list_diff that computes the difference of sets represented as sorted lists.
  2. is_unique in the provided code takes quadratic time – optimize it.

• Write functions compose and perform that take a list of functions and return their composition, i.e. a function compose [f1; …; fn] = x ↦ f1 (… (fn x)…) and perform [f1; …; fn] = x ↦ fn (… (f1 x)…).

• Write a solver for the Tents Puzzle http://www.mathsisfun.com/games/tents-puzzle.html.

• * Robot Squad. We are given a map of terrain with empty spaces and walls, and lidar readings for multiple robots, 8 readings of the distance to wall or another robot, for each robot. Robots are equipped with compasses, the lidar readings are in directions E, NE, N, NW, W, SW, S, SE. Determine the possible positions of robots.

• * Write a solver for the Plinx Puzzle http://www.mathsisfun.com/games/plinx-puzzle.html. It does not need to always return correct solutions but it should correctly solve the initial levels from the game.

Lecture 7: Laziness

Lazy evaluation. Stream processing.

M. Douglas McIlroy ‘‘Power Series, Power Serious’’

Oleg Kiselyov, Simon Peyton-Jones, Amr Sabry ‘‘Lazy v. Yield: Incremental, Linear Pretty-Printing’’

If you see any error on the slides, let me know!

1 Laziness

• Today’s lecture is about lazy evaluation.
• Thank you for coming, goodbye!
• But perhaps, do you have any questions?

2 Evaluation strategies and parameter passing

• Evaluation strategy is the order in which expressions are computed.

  • For the most part: when are arguments computed.

• Recall our problems with using flow control expressions like if_then_else in examples from \lambda-calculus lecture.

• There are many technical terms describing various strategies. Wikipedia:

  Strict evaluationArguments are always evaluated completely before function is applied. Non-strict evaluationArguments are not evaluated unless they are actually used in the evaluation of the function body. Eager evaluationAn expression is evaluated as soon as it gets bound to a variable. Lazy evaluationNon-strict evaluation which avoids repeating computation. Call-by-valueThe argument expression is evaluated, and the resulting value is bound to the corresponding variable in the function (frequently by copying the value into a new memory region). Call-by-referenceA function receives an implicit reference to a variable used as argument, rather than a copy of its value.

  • In purely functional languages there is no difference between the two strategies, so they are typically described as call-by-value even though implementations use call-by-reference internally for efficiency.
  • Call-by-value languages like C and OCaml support explicit references (objects that refer to other objects), and these can be used to simulate call-by-reference. Normal order Start computing function bodies before evaluating their arguments. Do not even wait for arguments if they are not needed. Call-by-nameArguments are substituted directly into the function body and then left to be evaluated whenever they appear in the function. Call-by-needIf the function argument is evaluated, that value is stored for subsequent uses.

• Almost all languages do not compute inside the body of un-applied function, but with curried functions you can pre-compute data before all arguments are provided.

  • Recall the search_bible example.

• In eager / call-by-value languages we can simulate call-by-name by taking a function to compute the value as an argument instead of the value directly.

  • ”Our” languages have a unit type with a single value () specifically for use as throw-away arguments.
  • Scala has a built-in support for call-by-name (i.e. direct, without the need to build argument functions).

• ML languages have built-in support for lazy evaluation.

• Haskell has built-in support for eager evaluation.

3 Call-by-name: streams

• Call-by-name is useful not only for implementing flow control

  • let ifthenelse cond e1 e2 = match cond with true -> e1 () | false -> e2 ()

  but also for arguments of value constructors, i.e. for data structures.

• Streams are lists with call-by-name tails.

  type ’a stream = SNil | SCons of ’a * (unit -> ’a stream)

• Reading from a stream into a list.

  let rec stake n = function | SCons (a, s) when n > 0 -> a::(stake (n-1) (s ())) | -> []

• Streams can easily be infinite.

  let rec sones = SCons (1, fun () -> sones)let rec sfrom n = SCons (n, fun () ->sfrom (n+1))

• Streams admit list-like operations.

  let rec smap f = function | SNil -> SNil | SCons (a, s) -> SCons (f a, fun () -> smap f (s ()))let rec szip = function | SNil, SNil -> SNil | SCons (a1, s1), SCons (a2, s2) -> SCons ((a1, a2), fun () -> szip (s1 (), s2 ())) | -> raise (Invalidargument “szip”)

• Streams can provide scaffolding for recursive algorithms:

  let rec sfib = SCons (1, fun () -> smap (fun (a,b)-> a+b) (szip (sfib, SCons (1, fun () -> sfib))))

  -3.45314-0.974534-3.85530493451515-0.297195396216431-3.262633946289190.020306918904617-3.89764-0.254862-3.876471755523220.464810160074084-3.241467125281120.930480222251621-2.33129-1.0592-2.60646249503903-0.276028575208361-2.267793358909910.0414737399126869-1.46345-0.9957-1.73862283370816-0.276028575208361-1.442287339595180.0626405609207567-1.73862-0.254862-2.013791506813070.676478370154782-1.548121444635531.03631432729197-2.62763-0.276029-2.796963884111650.507143802090224-2.373627463950261.0151475062839+-3.7833-0.582834+-2.55958-0.567776+-1.69025-0.5390640cm

• Streams are less functional than could be expected in context of input-output effects.

  let filestream name = let ch = openin name in let rec chreadline () =
  try SCons (inputline ch, chreadline) with Endoffile -> SNil in
  chreadline ()

• OCaml Batteries use a stream type enum for interfacing between various sequence-like data types.

  • The safest way to use streams in a linear / ephemeral manner: every value used only once.
  • Streams minimize space consumption at the expense of time for recomputation.

4 Lazy values

• Lazy evaluation is more general than call-by-need as any value can be lazy, not only a function parameter.

• A lazy value is a value that “holds” an expression until its result is needed, and from then on it “holds” the result.

  • Also called: a suspension. If it holds the expression, called a thunk.

• In OCaml, we build lazy values explicitly. In Haskell, all values are lazy but functions can have call-by-value parameters which “need” the argument.

• To create a lazy value: lazy expr – where expr is the suspended computation.

• Two ways to use a lazy value, be careful when the result is computed!

  • In expressions: Lazy.force l_expr
  • In patterns: match lexpr with lazy v -> …
    • Syntactically lazy behaves like a data constructor.

• Lazy lists:

  type ’a llist = LNil | LCons of ’a * ’a llist Lazy.t

• Reading from a lazy list into a list:

  let rec ltake n = function | LCons (a, lazy l) when n > 0 -> a::(ltake (n-1) l) | -> []

• Lazy lists can easily be infinite:

  let rec lones = LCons (1, lazy lones)let rec lfrom n = LCons (n, lazy (lfrom (n+1)))

• Read once, access multiple times:

  let filellist name = let ch = openin name in let rec chreadline () =
  try LCons (inputline ch, lazy (chreadline ())) with Endoffile -> LNil in chreadline ()

• let rec lzip = function | LNil, LNil -> LNil | LCons (a1, ll1), LCons (a2, ll2) -> LCons ((a1, a2), lazy ( lzip (Lazy.force ll1, Lazy.force ll2))) | -> raise (Invalidargument “lzip”)

  let rec lmap f = function | LNil -> LNil | LCons (a, ll) -> LCons (f a, lazy (lmap f (Lazy.force ll)))

• let posnums = lfrom 1let rec lfact = LCons (1, lazy (lmap (fun (a,b)-> a*b) (lzip (lfact, posnums))))

  -3.24858-1.02259-3.5449133483265-0.239416589495965-3.290911496229660.0569189046170128-2.40191-1.00142-2.65590686598756-0.281750231512105-2.380738192882660.0145852626008731-1.5129-0.980255-1.70339992062442-0.218249768487895-1.512898531551790.0145852626008731-0.327557-1.02259-0.772059796269348-0.0489152004233364-0.3063897340918110.1839198306654320.878952-1.022590.392115359174494-0.2394165894959650.6037835692551920.0780857256250827-3.56608-0.260583-3.629580632358780.691923534859108-3.33324513824581.03059267098823-2.67707-0.260583-2.69824050800370.734257176875248-2.42307183489881.0517594919963-1.7034-0.21825-1.872734488688980.670756713851039-1.555232173567931.0517594919963-0.77206-0.0489152-0.9413943643339070.903591744939807-0.6238920492128591.094093134012440.392115-0.2394170.2862812541341450.6284230718348990.6249503902632621.0517594919963-2.60922-0.546619-1.66302-0.503353-0.632667-0.50820.504955-0.500198*-3.48713460768869-0.5100825754830590cm

5 Power series and differential equations

• Differential equations idea due to Henning Thielemann. Just an example.

• Expression P (x) = \sum_{i = 0}^n a_{i} x^i defines a polynomial for n < \infty and a power series for n = \infty.

• If we define

  let rec lfoldright f l base = match l with | LNil -> base | LCons (a, lazy l) -> f a (lfoldright f l base)

  then we can compute polynomials

  let horner x l = lfoldright (fun c sum -> c +. x *. sum) l 0.

• But it will not work for infinite power series!

  • Does it make sense to compute the value at x of a power series?
  • Does it make sense to fold an infinite list?

• If the power series converges for x > 1, then when the elements a_{n} get small, the remaining sum \sum_{i = n}^{\infty} a_{i} x^i is also small.

• lfold_right falls into an infinite loop on infinite lists. We need call-by-name / call-by-need semantics for the argument function f.

  let rec lazyfoldr f l base = match l with | LNil -> base | LCons (a, ll) -> f a (lazy (lazyfoldr f (Lazy.force ll) base))

• We need a stopping condition in the Horner algorithm step:

  let lhorner x l =This is a bit of a hack, let upd c sum =we hope to ‘‘hit’’ the interval (0, \varepsilon]. if c = 0. || absfloat c > epsilonfloat then c +. x *. Lazy.force sum else 0. in lazyfoldr upd l 0.

  let invfact = lmap (fun n -> 1. /. floatofint n) lfactlet e = lhorner 1. invfact

5.1 Power series / polynomial operations

• let rec add xs ys = match xs, ys with | LNil, -> ys | , LNil -> xs | LCons (x,xs), LCons (y,ys) -> LCons (x +. y, lazy (add (Lazy.force xs) (Lazy.force ys)))
• let rec sub xs ys = match xs, ys with | LNil, -> lmap (fun x-> \sim-.x) ys | , LNil -> xs | LCons (x,xs), LCons (y,ys) ->
  LCons (x-.y, lazy (add (Lazy.force xs) (Lazy.force ys)))
• let scale s = lmap (fun x->s*.x)
• let rec shift n xs = if n = 0 then xs else if n > 0 then LCons (0. , lazy (shift (n-1) xs)) else match xs with | LNil -> LNil | LCons (0., lazy xs) -> shift (n+1) xs | -> failwith “shift: fractional division”
• let rec mul xs = function | LNil -> LNil | LCons (y, ys) -> add (scale y xs) (LCons (0., lazy (mul xs (Lazy.force ys))))
• let rec div xs ys = match xs, ys with | LNil, -> LNil | LCons (0., xs’), LCons (0., ys’) -> div (Lazy.force xs’) (Lazy.force ys’) | LCons (x, xs’), LCons (y, ys’) -> let q = x /. y in LCons (q, lazy (divSeries (sub (Lazy.force xs’) (scale q (Lazy.force ys’))) ys)) | LCons , LNil -> failwith “divSeries: division by zero”
• let integrate c xs = LCons (c, lazy (lmap (uncurry (/.)) (lzip (xs, posnums))))
• let ltail = function | LNil -> invalidarg “ltail” | LCons (, lazy tl) -> tl
• let differentiate xs = lmap (uncurry ( *.)) (lzip (ltail xs, posnums))

5.2 Differential equations

• \frac{\mathrm{d} \sin x}{\mathrm{d} x} = \cos x, \frac{\mathrm{d} \cos x}{\mathrm{d} x} = - \sin x, \sin 0 = 0, \cos 0 = 1.

• We will solve the corresponding integral equations. Why?

• We cannot define the integral by direct recursion like this:

  let rec sin = integrate (ofint 0) cosUnary op. let (\sim-:) =and cos = integrate (ofint 1) \sim-:sin lmap (fun x-> \sim-.x)

  unfortunately fails:

  Error: This kind of expression is not allowed as right-hand side of ‘let rec'

  • Even changing the second argument of integrate to call-by-need does not help, because OCaml cannot represent the values that x and y refer to.

• We need to inline a bit of integrate so that OCaml knows how to start building the recursive structure.

  let integ xs = lmap (uncurry (/.)) (lzip (xs, posnums))let rec sin = LCons (ofint 0, lazy (integ cos))and cos = LCons (ofint 1, lazy (integ \sim-:sin))

• The complete example would look much more elegant in Haskell.

• Although this approach is not limited to linear equations, equations like Lotka-Volterra or Lorentz are not “solvable” – computed coefficients quickly grow instead of quickly falling…

• Drawing functions are like in previous lecture, but with open curves.

• let plot1D f \simw \simscale \simtbeg \simtend = let dt = (tend -. tbeg) /. ofint w in Array.init w (fun i -> let y = lhorner (dt . ofint i) f in i, to_int (scale . y))

6 Arbitrary precision computation

• Putting it all together reveals drastic numerical errors for large x.

  let graph = let scale = ofint h /. ofint 8 in [plot1D sin \simw \simh0:(h/2) \simscale \simtbeg:(ofint 0) \simtend:(ofint 15),
  (250,250,0); plot1D cos \simw \simh0:(h/2) \simscale
  \simtbeg:(ofint 0) \simtend:(ofint 15), (250,0,250)]let () = drawtoscreen \simw \simh graph

  • Floating-point numbers have limited precision.
  • We break out of Horner method computations too quickly.

• For infinite precision on rational numbers we use the nums library.

  • It does not help – yet.

• Generate a sequence of approximations to the power series limit at x.

  let infhorner x l = let upd c sum = LCons (c, lazy (lmap (fun apx -> c+.x*.apx) (Lazy.force sum))) in lazyfoldr upd l (LCons (ofint 0, lazy LNil))

• Find where the series converges – as far as a given test is concerned.

  let rec exact f = functionWe arbitrarily decide that convergence is | LNil -> assert falsewhen three consecutive results are the same. | LCons (x0, lazy (LCons (x1, lazy (LCons (x2, ))))) when f x0 = f x1 && f x0 = f x2 -> f x0 | LCons (, lazy tl) -> exact f tl

• Draw the pixels of the graph at exact coordinates.

  let plot1D f \simw \simh0 \simscale \simtbeg \simtend = let dt = (tend -. tbeg) /. ofint w in let eval = exact (fun y-> toint (scale . y)) in Array.init w (fun i -> let y = infhorner (tbeg +. dt . ofint i) f in i, h0 + eval y)

• Success! If a power series had every third term contributing we would have to check three terms in the function exact…

  • We could like in lhorner test for f x0 = f x1 && not x0 =. x1

• Example n_chain: nuclear chain reaction–A decays into B decays into C

  • http://en.wikipedia.org/wiki/Radioactive_decay#Chain-decay_processes

  let nchain \simnA0 \simnB0 \simlA \simlB = let rec nA = LCons (nA0, lazy (integ (\sim-.lA :. nA))) and nB = LCons (nB0, lazy (integ (\sim-.lB :. nB +: lA *:. nA))) in nA, nB

7 Circular data structures: double-linked list

• Without delayed computation, the ability to define data structures with referential cycles is very limited.

• Double-linked lists contain such cycles between any two nodes even if they are not cyclic when following only forward or backward links.

  -5.517280.0390925-4.670607884640830.102592935573489-4.564773779600480.0602592935573488-4.1626-0.00324117-4.88227609472152-0.214909379547559-5.05161066278608-0.10907527450721-2.215260.0179257-1.516751554438420.229593861621908-1.410917449398070.123759756581558-0.987581-0.00324117-1.68608612250298-0.15140891652335-1.8130870485514-0.06674163249107020.9809330.01792571.615937954755920.1660933985976981.827606164836620.01792565154120922.20861-0.06674161.57360431273978-0.2784098425717691.40426974467522-0.151408916523354.198290.03909254.812127926974470.1872602196057684.981462495039030.1237597565815585.44713-0.0244084.74862746395026-0.172575737531424.5792928958857-0.151408916523350cm

• We need to “break” the cycles by making some links lazy.

• type ’a dllist = DLNil | DLCons of ’a dllist Lazy.t * ’a * ’a dllist

• let rec dldrop n l = match l with | DLCons (, x, xs) when n>0 -> dldrop (n-1) xs | -> l

• let dllistoflist l = let rec dllist prev l = match l with | [] -> DLNil | x::xs -> let rec cell = lazy (DLCons (prev, x, dllist cell xs)) in Lazy.force cell in dllist (lazy DLNil) l

• let rec dltake n l = match l with | DLCons (, x, xs) when n>0 -> x::dltake (n-1) xs | -> []

• let rec dlbackwards n l = match l with | DLCons (lazy xs, x, ) when n>0 -> x::dlbackwards (n-1) xs | -> []

8 Input-Output streams

• The stream type used a throwaway argument to make a suspension

  type ’a stream = SNil | SCons of ’a * (unit -> ’a stream)

  What if we take a real argument?

  type (’a, ’b) iostream = EOS | More of ’b * (’a -> (’a, ’b) iostream)

  A stream that for a single input value produces an output value.

• type ’a istream = (unit, ’a) iostreamInput stream produces output when “asked”.

  type ’a ostream = (’a, unit) iostreamOutput stream consumes provided input.

  • Sorry, the confusion arises from adapting the input file / output file terminology, also used for streams.

• We can compose streams: directing output of one to input of another.

  let rec compose sf sg = match sg with | EOS -> EOSNo more output.| More (z, g) -> match sf withNo more | EOS -> More (z, fun -> EOS)input ‘‘processing power’’. | More (y, f) -> let update x = compose (f x) (g y) in More (z, update)

  • Every box has one incoming and one outgoing wire: 0.02903822.280180.02903823257044581.41233959518455-0.03446220.459833-0.0344622304537637-0.492674295541738-0.0132954-1.40285-0.0132954094456939-2.228353618203470cm
  • Notice how the output stream is ahead of the input stream.

8.1 Pipes

• We need a more flexible input-output stream definition.

  • Consume several inputs to produce a single output.
  • Produce several outputs after a single input (or even without input).
  • No need for a dummy when producing output requires input.

• After Haskell, we call the data structure pipe.

  type (’a, ’b) pipe = EOP| Yield of ’b * (’a, ’b) pipeFor incremental streams change to lazy.|Await of ’a -> (’a, ’b) pipe

• Again, we can have producing output only input pipes and consuming input only output pipes.

  type ’a ipipe = (unit, ’a) pipetype voidtype ’a opipe = (’a, void) pipe

  • Why void rather than unit, and why only for opipe?

• Composition of pipes is like “concatenating them in space” or connecting boxes:

  let rec compose pf pg = match pg with | EOP -> EOPDone producing results. | Yield (z, pg’) -> Yield (z, compose pf pg’)Ready result. | Await g -> match pf with | EOP -> EOPEnd of input. | Yield (y, pf’) -> compose pf’ (g y)Compute next result. | Await f ->
  let update x = compose (f x) pg in Await updateWait for more input.

  let (>->) pf pg = compose pf pg

• Appending pipes means “concatenating them in time” or adding more fuel to a box:

  let rec append pf pg = match pf with | EOP -> pgWhen pf runs out, use pg.|Yield (z, pf’) -> Yield (z, append pf’ pg) | Await f ->If pf awaits input, continue when it comes. let update x = append (f x) pg in Await update

• Append a list of ready results in front of a pipe.

  let rec yieldall l tail = match l with | [] -> tail | x::xs -> Yield (x, yieldall xs tail)

• Iterate a pipe (not functional).

  let rec iterate f : ’a opipe = Await (fun x -> let () = f x in iterate

8.2 Example: pretty-printing

• Print hierarchically organized document with a limited line width.

  type doc = Text of string | Line | Cat of doc * doc | Group of doc

• let (++) d1 d2 = Cat (d1, Cat (Line, d2))let (!) s = Text slet testdoc =
  Group (!“Document” ++ Group (!“First part” ++ !“Second part”))

  # let () = printendline (pretty 30 testdoc);;
  DocumentFirst part Second part
  # let () = printendline (pretty 20 testdoc);;
  DocumentFirst partSecond part
  # let () = printendline (pretty 60 testdoc);;
  Document First part Second part

• Straightforward solution:

  let pretty w d =Allowed width of line w. let rec width = functionTotal length of subdocument. | Text z -> String.length z | Line -> 1 | Cat (d1, d2) -> width d1 + width d2 | Group d -> width d in
  let rec format f r = functionRemaining space r. | Text z -> z, r - String.length z | Line when f -> ” “, r-1If not f then line breaks. | Line ->”“, w | Cat (d1, d2) -> let s1, r = format f r d1 in let s2, r = format f r d2 in s1 s2, rIf following group fits, then without line breaks.| Group d -> format (f || width d <=

  18. r d in fst (format false w d)

• Working with a stream of nodes.

  type (’a, ’b) doce =Annotated nodes, special for group beginning. TE of ’a

  • string | LE of ’a | GBeg of ’b | GEnd of ’a

• Normalize a subdocument – remove empty groups.

  let rec norm = function | Group d -> norm d | Text “” -> None | Cat (Text ““, d) -> norm d | d -> Some d

• Generate the stream by infix traversal.

  let rec gen = function | Text z -> Yield (TE ((),z), EOP) | Line -> Yield (LE (), EOP) | Cat (d1, d2) -> append (gen d1) (gen d2) | Group d -> match norm d with | None -> EOP | Some d -> Yield (GBeg (), append (gen d) (Yield (GEnd (), EOP)))

• Compute lengths of document prefixes, i.e. the position of each node counting by characters from the beginning of document.

  let rec docpos curpos = Await (functionWe input from a doc_e pipe | TE (, z) -> Yield (TE (curpos, z),and output doc_e annotated with position. docpos (curpos + String.length z)) | LE ->Spice and line breaks increase position by 1. Yield (LE curpos, docpos (curpos + 1)) | GBeg ->Groups do not increase position. Yield (GBeg curpos, docpos curpos) | GEnd -> Yield (GEnd curpos, docpos curpos))

  let docpos = docpos 0The whole document starts at 0.

• Put the end position of the group into the group beginning marker, so that we can know whether to break it into multiple lines.

  let rec grends grstack = Await (function | TE | LE as e -> (match grstack with | [] -> Yield (e, grends [])We can yield only when | gr::grs -> grends ((e::gr)::grs))no group is waiting. | GBeg -> grends ([]::grstack)Wait for end of group. | GEnd endp -> match grstack withEnd the group on top of stack. | [] -> failwith “grends: unmatched group end marker” | [gr] ->Top group – we can yield now.
  yieldall (GBeg endp::List.rev (GEnd endp::gr)) (grends [])
  | gr::par::grs ->Remember in parent group instead. let par = GEnd endp::gr @ [GBeg endp] @ par in grends (par::grs))Could use catenable lists above.

• That’s waiting too long! We can stop waiting when the width of a group exceeds line limit. GBeg will not store end of group when it is irrelevant.

  let rec grends w grstack = let flush tail =When the stack exceeds width w, yieldallflush it – yield everything in it.(revconcatmap \simprep:(GBeg Toofar) snd grstack) tail inAbove: concatenate in rev. with prep before each part. Await (function | TE (curp, ) | LE curp as e -> (match grstack withRemember beginning of groups in the stack.
  | [] -> Yield (e, grends w []) | (begp, ):: when curp-begp > w -> flush (Yield (e, grends w [])) | (begp, gr)::grs -> grends w ((begp, e::gr)::grs)) | GBeg begp -> grends w ((begp, [])::grstack) | GEnd endp as e -> match grstack withNo longer fail when the stack is empty – | [] -> Yield (e, grends w [])could have been flushed. | (begp, ):: when endp-begp > w -> flush (Yield (e, grends w [])) | [, gr] ->If width not exceeded, yieldallwork as before optimization.(GBeg (Pos endp)::List.rev (GEnd endp::gr)) (grends w []) | (, gr)::(parbegp, par)::grs ->
  let par = GEnd endp::gr @ [GBeg (Pos endp)] @ par in grends w ((parbegp, par)::grs))

• Initial stack is empty:

  let grends w = grends w []

• Finally we produce the resulting stream of strings.

  let rec format w (inline, endlpos as st) =State: the stack of Await (function‘‘group fits in line’’; position where end of line would be. | TE (, z) -> Yield (z, format w st) | LE p when List.hd inline ->
  Yield (” “, format w st)After return, line has w free space. | LE p -> Yield (”“, format w (inline, p+w)) | GBeg Toofar ->Group with end too far is not inline. format w (false::inline, endlpos) | GBeg (Pos p) ->Group is inline if it ends soon enough. format w ((p<=endlpos)::inline, endlpos) | GEnd -> format w (List.tl inline, endlpos))

  let format w = format w ([false], w)Break lines outside of groups.

• Put the pipes together:

  let prettyprint w doc =

  -7.32332-0.0176611-6.8788199497288-0.0176610662786083-4.10597-0.0176611-3.64029633549411-0.0176610662786083-0.1477710.003505750.2755655509988090.003505754729461573.76809-0.01766114.233761079507870.003505754729461570cm

• Factorize format so that various line breaking styles can be plugged in.

  let rec breaks w (inline, endlpos as st) = Await (function | TE as e -> Yield (e, breaks w st) | LE p when List.hd inline -> Yield (TE (p, ” “), breaks w st) | LE p as e -> Yield (e, breaks w (inline, p+w)) | GBeg Toofar as e -> Yield (e, breaks w (false::inline, endlpos)) | GBeg (Pos p) as e -> Yield (e, breaks w ((p<=endlpos)::inline, endlpos)) | GEnd as e -> Yield (e, breaks w (List.tl inline, endlpos)))let breaks w = breaks w ([false], w)
  let rec emit = Await (function | TE (, z) -> Yield (z, emit) | LE -> Yield (”n”, emit) | GBeg | GEnd -> emit)let prettyprint w doc = gen doc >-> docpos >-> grends w >-> breaks w >-> emit >-> iterate printstring

• Tests.

  let (++) d1 d2 = Cat (d1, Cat (Line, d2))let (!) s = Text slet testdoc =
  Group (!“Document” ++ Group (!“First part” ++ !“Second part”))let printedoc prp prep = function | TE (p,z) -> prp p; printendline (“:”z) | LE p -> prp p; printendline “: endline” | GBeg ep -> prep ep; printendline “: GBeg” | GEnd p -> prp p; printendline “: GEnd”let noop () = ()let printpos = function | Pos p -> printint p | Toofar -> printstring “Too far”let = gen testdoc >-> iterate (printedoc noop noop)let = gen testdoc >-> docpos >-> iterate (printedoc printint printint)let = gen testdoc >-> docpos >-> grends 20 >-> iterate (printedoc printint printpos)let = gen testdoc >-> docpos >-> grends 30 >-> iterate (printedoc printint printpos)let = gen testdoc >-> docpos >-> grends 60 >-> iterate (printedoc printint printpos)let = prettyprint 20 testdoclet = prettyprint 30 testdoclet = prettyprint 60 testdoc

Functional Programming

Streams and lazy evaluation

Exercise 1: My first impulse was to define lazy list functions as here:

let rec wrong_lzip = function | LNil, LNil -> LNil | LCons (a1, lazy l1), LCons (a2, lazy l2) -> LCons ((a1, a2), lazy (wrong_lzip (l1, l2))) | -> raise (Invalidargument “lzip”)let rec wrong_lmap f = function | LNil -> LNil | LCons (a, lazy l) -> LCons (f a, lazy (wrong_lmap f l))

What is wrong with these definitions – for which edge cases they do not work as intended?

Exercise 2: Cyclic lazy lists:

1. Implement a function *cycle : 'a list -> 'a llist* that creates a lazy list with elements from standard list, and the whole list as the tail after the last element from the input list.

   *[a1; a2; …; aN]\mapsto

   		…

   -1.407730.189096-0.9632226484984790.210262600873131-0.2012170.1890960.2644529699695730.2102626008731310.751290.1890961.068792168276230.1890957798650621.788460.1890962.190633681703930.2102626008731312.19063368170393-0.191906998280196-2.0-0.2-2.0003968778939-0.001405609207567140cm*

   Your function cycle can either return LNil or fail for an empty list as argument. 1. Note that *inv_fact* from the lecture defines the power series for the \exp (\cdot) function (\exp (x) = e^x). Using *cycle* and *inv_fact*, define the power series for \sin (\cdot) and \cos (\cdot), and draw their graphs using helper functions from the lecture script *Lec7.ml*.

   Exercise 3: * Modify one of the puzzle solving programs (either from the previous lecture or from your previous homework) to work with lazy lists. Implement the necessary higher-order lazy list functions. Check that indeed displaying only the first solution when there are multiple solutions in the result takes shorter than computing solutions by the original program.

   Exercise 4: Hamming’s problem. Generate in increasing order the numbers of the form 2^{a_{1}} 3^{a_{2}} 5^{a_{3}} \ldots p_{k}^{a_{k}}, that is numbers not divisible by prime numbers greater than the kth prime number.

   • In the original Hamming’s problem posed by Dijkstra, k = 3*, which is related

   to* http://en.wikipedia.org/wiki/Regular_number.

   Starter code is available in the middle of the lecture script Lec7.ml:let rec lfilter f = function | LNil -> LNil | LCons (n, ll) -> if f n then LCons (n, lazy (lfilter f (Lazy.force ll))) else lfilter f (Lazy.force ll)let primes = let rec sieve = function LCons(p,nf) -> LCons(p, lazy (sieve (sift p (Lazy.force nf)))) | LNil -> failwith “Impossible! Internal error.” and sift p = lfilter (function n -> n mod p <> 0)in sieve (lfrom 2)let times ll n = lmap (fun i -> i n) ll;;let rec merge xs ys = match xs, ys with | LCons (x, lazy xr), LCons (y, lazy yr) -> if x < y then LCons (x, lazy (merge xr ys)) else if x > y then LCons (y, lazy (merge xs yr)) else LCons (x, lazy (merge xr yr)) | r, LNil | LNil, r -> rlet hamming k = let pr = ltake k primes in let rec h = LCons (1, lazy ( )) in h*

   Exercise 5: Modify format and/or breaks to use just a single number instead of a stack of booleans to keep track of what groups should be inlined.

   Exercise 6: Add indentation to the pretty-printer for groups: if a group does not fit in a single line, its consecutive lines are indented by a given amount tab of spaces deeper than its parent group lines would be. For comparison, let’s do several implementations.

   1. Modify the straightforward implementation of *pretty*.
   2. Modify the first pipe-based implementation of *pretty* by modifying the *format* function.
   3. Modify the second pipe-based implementation of *pretty* by modifying the *breaks* function. Recover the positions of elements – the number of characters from the beginning of the document – by keeping track of the growing offset.
   4. ** Modify a pipe-based implementation to provide a different style of indentation: indent the first line of a group, when the group starts on a new line, at the same level as the consecutive lines (rather than at the parent level of indentation).*

   Exercise 7: Write a pipe that takes document elements annotated with linear position, and produces document elements annotated with (line, column) coordinates.

   Write another pipe that takes so annotated elements and adds a line number indicator in front of each line. Do not update the column coordinate. Test the pipes by plugging them before the emit pipe.

   1: first line
   2: second line, etc.

   Exercise 8: Write a pipe that consumes document elements doc_e and yields the toplevel subdocuments doc which would generate the corresponding elements.

   You can modify the definition of documents to allow annotations, so that the element annotations are preserved (gen should ignore annotations to keep things simple):type ’a doc = Text of ’a string | Line of ’a | Cat of doc * doc | Group of ’a * doc*

   Exercise 9: * Design and implement a way to duplicate arrows outgoing from a pipe-box, that would memoize the stream, i.e. not recompute everything “upstream” for the composition of pipes. Such duplicated arrows would behave nicely with pipes reading from files.

   *

   Does not recompute g nor f.				Reads once and passes all content to f and g.

   -5.769180.217059-4.245171318957530.217059134806191-3.800670.238226-2.44599153327160.746229660007938-3.821830.259393-2.4459915332716-0.2909445693874851.088870.2170593.988722053181640.7250628389998681.046530.1958923.96755523217357-0.3332782114036250cm*

   Lecture 8: Monads

   List comprehensions. Basic monads; transformers. Probabilistic Programming.Lightweight cooperative threads.

   Some examples from Tomasz Wierzbicki. Jeff Newbern ‘‘All About Monads’‘.M. Erwig, S. Kollmansberger ‘‘Probabilistic Functional Programming in Haskell’‘.Jerome Vouillon ‘‘Lwt: a Cooperative Thread Library’’.

   If you see any error on the slides, let me know!

   1 List comprehensions

   • Recall the awkward syntax we used in the Countdown Problem example:

     • Brute-force generation:

       let combine l r = List.map (fun o->App (o,l,r)) [Add; Sub; Mul; Div]let rec exprs = function | [] -> [] | [n] -> [Val n] | ns -> split ns |-> (fun (ls,rs) -> exprs ls |-> (fun l -> exprs rs |-> (fun r -> combine l r)))

     • Genarate-and-test scheme:

       let guard p e = if p e then [e] else []let solutions ns n = choices ns |-> (fun ns’ -> exprs ns’ |-> guard (fun e -> eval e = Some n))

   • Recall that we introduced the operator

     let ( |-> ) x f = concatmap f x

   • We can do better with list comprehensions syntax extension.

     #load “dynlink.cma”;;#load “camlp4o.cma”;;#load “Camlp4Parsers/Camlp4ListComprehension.cmo”;;

     let test = [i * 2 | i <- fromto 2 22; i mod 3 = 0]

   • What it means:

     • [expr | ] can be translated as [expr]

     • [expr | v <- generator; more] can be translated as

       generator |-> (fun v -> translation of [expr | more])

     • [expr | condition; more] can be translated as

       if condition then translation of [expr | more] else []

   • Revisiting the Countdown Problem code snippets:

     • Brute-force generation:

       let rec exprs = function | [] -> [] | [n] -> [Val n] | ns -> [App (o,l,r) | (ls,rs) <- split ns; l <- exprs ls; r <- exprs rs; o <- [Add; Sub; Mul; Div]]

     • Genarate-and-test scheme:

       let solutions ns n = [e | ns’ <- choices ns; e <- exprs ns’; eval e = Some n]

   • Subsequences using list comprehensions (with garbage):

     let rec subseqs l = match l with | [] -> [[]] | x::xs -> [ys | px <- subseqs xs; ys <- [px; x::px]]

   • Computing permutations using list comprehensions:

     • via insertion

       let rec insert x = function | [] -> [[x]] | y::ys’ as ys ->
       (x::ys) :: [y::zs | zs <- insert x ys’]let rec insperms = function | [] -> [[]] | x::xs -> [zs | ys <- insperms xs; zs <- insert ys]

     • via selection

       let rec select = function | [x] -> [x,[]] | x::xs -> (x,xs) :: [ y, x::ys | y,ys <- select xs]let rec selperms = function | [] -> [[]] | xs -> [x::ys | x,xs’ <- select xs; ys <- selperms xs’]

   2 Generalized comprehensions aka. do-notation

   • We need to install the syntax extension pa_monad

     • by copying the pa_monad.cmo or pa_monad400.cmo (for OCaml 4.0) file from the course page,
     • or if it does not work, by compiling from sources at http://www.cas.mcmaster.ca/~carette/pa_monad/and installing under a Unix-like shell (Windows: the Cygwin shell).
       • Under Debian/Ubuntu, you may need to install camlp4-extras

   • let rec exprs = function | [] -> [] | [n] -> [Val n] | ns ->
     perform with (|->) in (ls,rs) <– split ns; l <– exprs ls; r <– exprs rs; o <– [Add; Sub; Mul; Div];
     [App (o,l,r)]

   • The perform syntax does not seem to support guards…

     let solutions ns n = perform with (|->) in ns’ <– choices ns;
     e <– exprs ns’; eval e = Some n; e

       eval e = Some n;      Error: This expression has type bool but an 

     expression was expected of type ’a list

   • So it wants a list… What can we do?

   • We can decide whether to return anything

     let solutions ns n = perform with (|->) in ns’ <– choices ns;
     e <– exprs ns’; if eval e = Some n then [e] else []

   • But what if we want to check earlier…

     General “guard check” function

     let guard p = if p then [()] else []

   • let solutions ns n = perform with (|->) in ns’ <– choices ns;
     e <– exprs ns’; guard (eval e = Some n); [e]

   3 Monads

   • A polymorphic type 'a monad (or 'a Monad.t, etc.) that supports at least two operations:

     • bind : 'a monad -> ('a -> 'b monad) -> 'b monad
     • return : 'a -> 'a monad

     • = is infix syntax for bind: let (>>=) a b = bind a b

   • With bind in scope, we do not need the with clause in perform

     let bind a b = concatmap b alet return x = [x] let solutions ns n =
     perform ns’ <– choices ns; e <– exprs ns’; guard (eval e = Some n); return e

   • Why guard looks this way?

     let fail = []let guard p = if p then return () else fail

     • Steps in monadic computation are composed with >>=, e.g. |->
       • as if ; was replaced by >>=
     • [] |-> … does not produce anything – as needed by guarding
     • [()] |-> … \rightsquigarrow (fun _ -> …) () \rightsquigarrow … i.e. keep without change

   • Throwing away the binding argument is a common practice, with infix syntax >> in Haskell, and supported in do-notation and perform.

   • Everything is a monad?

   • Different flavors of monads?

   • Can guard be defined for any monad?

   • perform syntax in depth:

     		exp
     []
     		but uses b instead of bind
     		and f instead of failwith
     		during translation

   • It can be useful to redefine: let failwith = fail (why?)

   3.1 Monad laws

   • A parametric data type is a monad only if its bind and return operations meet axioms:

     \begin{matrix} \operatorname{bind} (\operatorname{return}a) f & \approx & f a\\\\\\ \operatorname{bind}a (\lambda x.\operatorname{return}x) & \approx & a \\\\\\ \operatorname{bind} (\operatorname{bind}a (\lambda x.b)) (\lambda y.c) & \approx & \operatorname{bind}a (\lambda x.\operatorname{bind}b (\lambda y.c)) \end{matrix}

   • Check that the laws hold for our example monad

     let bind a b = concatmap b alet return x = [x]

   3.2 Monoid laws and monad-plus

   • A monoid is a type with, at least, two operations

     • mzero : 'a monoid
     • mplus : 'a monoid -> 'a monoid -> 'a monoid

     that meet the laws:

     \begin{matrix} \operatorname{mplus}\operatorname{mzero}a & \approx & a \\\\\\ \operatorname{mplus}a\operatorname{mzero} & \approx & a \\\\\\ \operatorname{mplus}a (\operatorname{mplus}b c) & \approx & \operatorname{mplus} (\operatorname{mplus}a b) c \end{matrix}

   • We will define fail as synonym for mzero and infix ++ for mplus.

   • Fusing monads and monoids gives the most popular general flavor of monads which we call monad-plus after Haskell.

   • Monad-plus requires additional axioms that relate its “addition” and its “multiplication”.

     \begin{matrix} \operatorname{bind}\operatorname{mzero}f & \approx & \operatorname{mzero}\\\\\\ \operatorname{bind}m (\lambda x.\operatorname{mzero}) & \approx & \operatorname{mzero} \end{matrix}

   • Using infix notation with \oplus as mplus, \boldsymbol{0} as mzero, \vartriangleright as bind and \boldsymbol{1} as return, we get monad-plus axioms

     \begin{matrix} \boldsymbol{0} \oplus a & \approx & a \\\\\\ a \oplus \boldsymbol{0} & \approx & a \\\\\\ a \oplus (b \oplus c) & \approx & (a \oplus b) \oplus c\\\\\\ \boldsymbol{1}x \vartriangleright f & \approx & f x\\\\\\ a \vartriangleright \lambda x.\boldsymbol{1}x & \approx & a \\\\\\ (a \vartriangleright \lambda x.b) \vartriangleright \lambda y.c & \approx & a \vartriangleright (\lambda x.b \vartriangleright \lambda y.c)\\\\\\ \boldsymbol{0} \vartriangleright f & \approx & \boldsymbol{0}\\\\\\ a \vartriangleright (\lambda x.\boldsymbol{0}) & \approx & \boldsymbol{0} \end{matrix}

   • The list type has a natural monad and monoid structure

     let mzero = [] let mplus = (@) let bind a b = concatmap b a let return a = [a]

   • We can define in any monad-plus

     let fail = mzero let failwith = fail let (++) = mplus let (>>=) a b = bind a b let guard p = if p then return () else fail

   3.3 Backtracking: computation with choice

   We have seen mzero, i.e. fail in the countdown problem. What about mplus?

   let findtoeat n islandsize numislands emptycells = let honey = honeycells n emptycells in let rec findboard s = (* Printf.printf “findboard: %sn” (statestr s); ) match visitcell s with | None -> perform
   guard (s.beenislands = numislands); return s.eaten | Some (cell, s) -> perform s <– findisland cell (freshisland s);
   guard (s.beensize = islandsize); findboard s and findisland current s = let s = keepcell current s in neighbors n emptycells current
   |> foldM (fun neighbor s -> if CellSet.mem neighbor s.visited then return s else let chooseeat =
   if s.moretoeat <= 0 then fail else return (eatcell neighbor s) and choosekeep = if s.beensize >= islandsize then fail else findisland neighbor s in mplus chooseeat choosekeep) s in let cellstoeat = List.length honey - islandsize numislands in findboard (initstate honey cellstoeat)

   4 Monad “flavors”

   • Monads “wrap around” a type, but some monads need an additional type parameter.
     • Usually the additional type does not change while within a monad – we will therefore stick to 'a monad rather than parameterize with an additional type ('s, 'a) monad.
   • As monad-plus shows, things get interesting when we add more operations to a basic monad (with bind and return).

     • Monads with access:

       access : ’a monad -> ’a

       Example: the lazy monad.

     • Monad-plus, non-deterministic computation:

       mzero : 'a monad``mplus : 'a monad -> 'a monad -> 'a monad

     • Monads with environment or state – parameterized by type store:

       get : store monadput : store -> unit monad

       There is a “canonical” state monad. Similar monads: the writer monad (with get called listen and put called tell); the reader monad, without put, but with get (called ask) and local:

       local : (store -> store) -> ’a monad -> ’a monad

     • The exception / error monads – parameterized by type excn:

       throw : excn -> ’a monadcatch : ’a monad -> (excn -> ’a monad) -> ’a monad

     • The continuation monad:

       callCC : ((’a -> ’b monad) -> ’a monad) -> ’a monad

       We will not cover it.

     • Probabilistic computation:

       choose : float -> ’a monad -> ’a monad -> ’a monad

       satisfying the laws with a \oplus _{p} b for choose p a b and pq for p*.q, 0 \leqslant p, q \leqslant 1:

       \begin{matrix} a \oplus _{0} b & \approx & b \\\\\\ a \oplus _{p} b & \approx & b \oplus _{1 - p} a\\\\\\ a \oplus _{p} (b \oplus _{q} c) & \approx & \left( a \oplus _{\frac{p}{p + q - pq}} b \right) \oplus _{p + q - pq} c\\\\\\ a \oplus _{p} a & \approx & a \end{matrix}

     • Parallel computation as monad with access and parallel bind:

       parallel :’a monad-> ’b monad-> (’a -> ’b -> ’c monad) -> ’c monad

       Example: lightweight threads.

   5 Interlude: the module system

   • I provide below much more information about the module system than we need, just for completeness. You can use it as reference.

     • Module system details will not be on the exam – only the structure / signature definitions as discussed in lecture 5.

   • Modules collect related type definitions and operations together.

   • Module “values” are introduced with struct … end – structures.

   • Module types are introduced with sig … end – signatures.

     • A structure is a package of definitions, a signature is an interface for packages.

   • A source file source.ml or Source.ml defines a module Source.

     A source file source.mli or Source.mli defines its type.

   • We can create the initial interface by entering the module in the interactive toplevel or by command ocamlc -i source.ml

   • In the “toplevel” – accurately, module level – modules are defined with module ModuleName = … or module ModuleName : MODULE_TYPE = … syntax, and module types with module type MODULETYPE = … syntax.

     • Corresponds to let v_name = … resp. let v_name : v_type = … syntax for values and type vtype = … syntax for types.

   • Locally in expressions, modules are defined with let module M = … in … syntax.

     • Corresponds to let v_name = … in … syntax for values.

   • The content of a module is made visible in the remainder of another module by open Module

     • Module Pervasives is initially visible, as if each file started with open Pervasives.

   • The content of a module is made visible locally in an expression with let open Module in … syntax.

   • Content of a module is included into another module – i.e. made part of it – by include Module.

     • Just having open Module inside Parent does not affect how Parent looks from outside.

   • Module functions – functions from modules to modules – are called functors (not the Haskell ones!). The type of the parameter has to be given.

     module Funct = functor (Arg : sig … end) -> struct … end

     module Funct (Arg : sig … end) = struct … end

     • Functors can return functors, i.e. modules can be parameterized by multiple modules.
     • Modules are either structures or functors.
     • Different kind of thing than Haskell functors.

   • Functor application always uses parentheses: Funct (struct … end)

   • We can use named module type instead of signature and named module instead of structure above.

   • Argument structures can contain more definitions than required.

   • A signature MODULETYPE with type t_name = … is like MODULETYPE but with t_name made more specific.

   • We can also include signatures into other signatures, by include MODULETYPE.

     • include MODULETYPE with type tname := … will substitute type t_name with provided type.

   • Modules, just as expressions, are not recursive or mutually recursive by default. Syntax for recursive modules:module rec ModuleName : MODULETYPE = … and …

   • We can recover the type – i.e. signature – of a module bymodule type of Module

   • Finally, we can pass around modules in normal functions.

     • (module Module) is an expression
     • (val modulev) is a module

     • # module type T = sig val g : int -> int endlet f modv x =  let module 
       M = (val modv : T) in  M.g x;;
       
       val f : (module T) -> int -> int = <fun>
       
       # let test = f (module struct let g i = i*i end : T);;
       
       val test : int -> int = <fun>

   6 The two metaphors

   • Monads can be seen as containers: 'a monad contains stuff of type 'a
   • and as computation: 'a monad is a special way to compute 'a.
     • A monad fixes the sequence of computing steps – unless it is a fancy monad like parallel computation monad.

   6.1 Monads as containers

   • A monad is a quarantine container:

     • we can put something into the container with return

     • we can operate on it, but the result needs to stay in the container

       let lift f m = perform x <– m; return (f x) val lift : (’a -> ’b) -> ’a monad -> ’b monad

     • We can deactivate-unwrap the quarantine container but only when it is in another container so the quarantine is not broken

       let join m = perform x <– m; x val join : (’a monad) monad -> ’a monad

   • The quarantine container for a monad-plus is more like other containers: it can be empty, or contain multiple elements.
   • Monads with access allow us to extract the resulting element from the container, other monads provide a run operation that exposes “what really happened behind the quarantine”.

   6.2 Monads as computation

   • To compute the result, perform instructions, naming partial results.

   • Physical metaphor: assembly line

     -5.762933.70556.069321338801433.72666688715439-5.72061.990996.217489085857921.990987564492666.069323.726678.926842174890862.7741599417912410.0486836883186-0.1045277153062576.217491.990996.386823653922481.736985712395826.76782643206773-0.08336089429818766.76783-0.0833609-5.29726154253208-0.1045277153062576.72549-1.84021-5.19142743749173-1.819040216959920.6717822.879992.3016271993652.879994046831597.720331.863998.12250297658420.7209783040084676.00582-0.9723674.69347797327689-0.9723673766371212.06879-0.9088670.735282444767826-0.908866913612912-5.762932.87999-4.619923270273852.87999404683159-4.42942-0.930034-5.53009657362085-0.930033734620982-9.763462.68949-8.324116946686072.26615623759757-7.308109538298720.9749801561053052.280462.371993.175100860066451.990988185174813.656303743881470.9749801561053053.88914-1.289873.31763460775235-2.263543458129383.29646778674428-2.83504762534727-4.26009-1.18404-4.64394551581309-1.82001279007382-4.72575737531419-2.72921352030692w-7.42741.25543c3.596731.32033c'3.5293-2.47521c''-4.93743-1.586216.280990.911486.76783-0.0833609-4.408260.91148-3.916971543196911.990989632039070.206112-2.89855-0.600035853371303-1.827196584929880cm

     let assemblyLine w = perform c <– makeChopsticks w c’ <– polishChopsticks c c’’ <– wrapChopsticks c’ return c’’

   • Any expression can be spread over a monad, e.g. for \lambda-terms:

     \begin{matrix} \llbracket N \rrbracket = & \operatorname{return}N & \text{(constant)}\\\\\\ \llbracket x \rrbracket = & \operatorname{return}x & \text{(variable)}\\\\\\ \llbracket \lambda x.a \rrbracket = & \operatorname{return} (\lambda x. \llbracket a \rrbracket) & \text{(function)}\\\\\\ \llbracket \operatorname{let}x = a\operatorname{in}b \rrbracket = & \operatorname{bind} \llbracket a \rrbracket (\lambda x. \llbracket b \rrbracket) & \text{(local definition)}\\\\\\ \llbracket a b \rrbracket = & \operatorname{bind} \llbracket a \rrbracket (\lambda v_{a} .\operatorname{bind} \llbracket b \rrbracket (\lambda v_{b} .v_{a} v_{b})) & \text{(application)} \end{matrix}

   • When an expression is spread over a monad, its computation can be monitored or affected without modifying the expression.

   7 Monad classes

   • To implement a monad we need to provide the implementation type, return and bind operations.

     module type MONAD = sig type ’a t val return : ’a -> ’a t val bind : ’a t -> (’a -> ’b t) -> ’b tend

     • Alternatively we could start from return, lift and join operations.

       • For monads that change their additional type parameter we could define: module type MONAD = sig type (’s, ’a) t val return : ’a -> (’s, ’a) t val bind : (’s, ’a) t -> (’a -> (’s, ’b) t) -> (’s, ’b) tend

   • Based on just these two operations, we can define a whole suite of general-purpose functions. We look at just a tiny selection.

     module type MONADOPS = sig type ’a monad include MONAD with type ’a t := ’a monad val ( >>= ) :’a monad -> (’a -> ’b monad) -> ’b monad val foldM : (’a -> ’b -> ’a monad) -> ’a -> ’b list -> ’a monad val whenM : bool -> unit monad -> unit monad
     val lift : (’a -> ’b) -> ’a monad -> 'b monad val (>>|) : ’a monad -> (’a -> ’b) -> ’b monadval join : ’a monad monad -> ’a monad val ( >=> ) : (’a ->’b monad) -> (’b ->’c monad) -> ’a -> ’c monadend

   • Given a particular implementation, we define these functions.

     module MonadOps (M : MONAD) = struct open M type ‘a monad = ’a t let run x = x let (>>=) a b = bind a b let rec foldM f a = function | [] -> return a | x::xs -> f a x >>= fun a’ -> foldM f a’ xs let whenM p s = if p then s else return () let lift f m = perform x <– m; return (f x) let (>>|) a b = lift b a let join m = perform x <– m; x let (>=>) f g = fun x -> f x >>= gend

   • We make the monad “safe” by keeping its type abstract. But run exposes “what really happened”.

     module Monad (M : MONAD) :sig include MONADOPS val run : ’a monad -> ’a M.tend = struct include M include MonadOps(M)end

     • Our run function does not do anything at all. Often more useful functions are called run but then they need to be defined for each implementation separately. Our access operation (see section on monad flavors) is often called run.

   • The monad-plus class of monads has a lot of implementations. They need to provide mzero and mplus.

     module type MONADPLUS = sig include MONAD val mzero : ’a t val mplus : ’a t -> ’a t -> ’a tend

   • Monad-plus class also has its general-purpose functions:

     module type MONADPLUSOPS = sig include MONADOPS val mzero : ’a monad val mplus : ’a monad -> ’a monad -> ’a monad val fail : ’a monad val (++) : ’a monad -> ’a monad -> ’a monad val guard : bool -> unit monad val msummap : (’a -> ’b monad) -> ’a list -> ’b monadend

   • We again separate the “implementation” and the “interface”.

     module MonadPlusOps (M : MONADPLUS) = struct open M include MonadOps(M)
     let fail = mzero let (++) a b = mplus a b let guard p = if p then return () else fail let msummap f l = List.foldright (fun a acc -> mplus (f

     1. acc) l mzeroend

     module MonadPlus (M : MONADPLUS) :sig include MONADPLUSOPS val run : ’a monad -> ’a M.tend = struct include M include MonadPlusOps(M)end

   • We also need a class for computations with state.

     module type STATE = sig type store type ’a t val get : store t val put : store -> unit tend

     The purpose of this signature is inclusion in other signatures.

   8 Monad instances

   • We do not define a class for monads with access since accessing means running the monad, not useful while in the monad.

   • Notation for laziness heavy? Try a monad! (Monads with access.)

     module LazyM = Monad (struct type ’a t = ’a Lazy.t let bind a b = lazy (Lazy.force (b (Lazy.force a))) let return a = lazy aend)

     let laccess m = Lazy.force (LazyM.run m)

   • Our resident list monad. (Monad-plus.)

     module ListM = MonadPlus (struct type ’a t = ’a list let bind a b = concatmap b a let return a = [a] let mzero = [] let mplus = List.appendend)

   8.1 Backtracking parameterized by monad-plus

   module Countdown (M : MONADPLUSOPS) = struct open MOpen the module to make monad operations visible.

   let rec insert x = functionAll choice-introducing operations | [] -> return [x]need to happen in the monad. | y::ys as xs -> return (x::xs) ++ perform xys <– insert x ys; return (y::xys)

   let rec choices = function | [] -> return [] | x::xs -> perform cxs <– choices xs;Choosing which numbers in what order
   return cxs ++ insert x cxsand now whether with or without x.

   type op = Add | Sub | Mul | Div

   let apply op x y = match op with | Add -> x + y | Sub -> x - y | Mul -> x * y | Div -> x / y

   let valid op x y = match op with | Add -> x <= y | Sub -> x > y | Mul -> x <= y && x <> 1 && y <> 1 | Div -> x mod y = 0 && y <> 1

   type expr = Val of int | App of op * expr * expr

   let op2str = function | Add -> “+” | Sub -> “-” | Mul -> “*” | Div -> “/” let rec expr2str = functionWe will provide solutions as strings. | Val n -> stringofint n | App (op,l,r) ->“(”expr2str lop2str opexpr2str r”)”

   let combine (l,x) (r,y) o = performTry out an operator. guard (valid o x y); return (App (o,l,r), apply o x y)

   let split l =Another choice: which numbers go into which argument. let rec aux lhs = function | [] | [] -> failBoth arguments need numbers.| [y; z] -> return (List.rev (y::lhs), [z]) | hd::rhs ->
   let lhs = hd::lhs in return (List.rev lhs, rhs) ++ aux lhs rhs in aux [] l

   let rec results = functionBuild possible expressions once numbers | [] -> failhave been picked.| [n] -> perform guard (n > 0); return (Val n, n) | ns -> perform (ls, rs) <– split ns; lx <– results ls; ly <– results rs;Collect solutions using each operator. msummap (combine lx ly) [Add; Sub; Mul; Div]

   let solutions ns n = performSolve the problem: ns’ <– choices ns;pick numbers and their order, (e,m) <– results ns’;build possible expressions, guard (m=n);check if the expression gives target value, return (expr2str e)‘‘print’’ the solution.end

   8.2 Understanding laziness

   • We will measure execution times:

     #load “unix.cma”;;let time f = let tbeg = Unix.gettimeofday () in let res = f () in let tend = Unix.gettimeofday () in tend -. tbeg, res

   • Let’s check our generalized Countdown solver using original operations.

     module ListCountdown = Countdown (ListM)let test1 () = ListM.run (ListCountdown.solutions [1;3;7;10;25;50] 765)let t1, sol1 = time test1

   • val t1 : float = 2.2856600284576416val sol1 : string list =
     [“((25-(3+7))(1+50))”; ”(((25-3)-7)(1+50))”; …

   • What if we want only one solution? Laziness to the rescue!

     type ’a llist = LNil | LCons of ’a * ’a llist Lazy.tlet rec ltake n = function | LCons (a, lazy l) when n > 0 -> a::(ltake (n-1) l) | -> []let rec lappend l1 l2 = match l1 with LNil -> l2 | LCons (hd, tl) -> LCons (hd, lazy (lappend (Lazy.force tl) l2))let rec lconcatmap f = function | LNil -> LNil | LCons (a, lazy l) ->
     lappend (f a) (lconcatmap f l)

   • That is, another monad-plus.

     module LListM = MonadPlus (struct type ’a t = ’a llist let bind a b = lconcatmap b a let return a = LCons (a, lazy LNil) let mzero = LNil let mplus = lappendend)

   • module LListCountdown = Countdown (LListM)let test2 () = LListM.run (LListCountdown.solutions [1;3;7;10;25;50] 765)

   • # let t2a, sol2 = time test2;;val t2a : float = 2.51197600364685059val 
     sol2 : string llist = LCons ("((25-(3+7))*(1+50))", <lazy>)

     Not good, almost the same time to even get the lazy list!

   • # let t2b, sol21 = time (fun () -> ltake 1 sol2);;val t2b : float 
     = 2.86102294921875e-06val sol21 : string list = ["((25-(3+7))*(1+50))"]# 
     let t2c, sol29 = time (fun () -> ltake 10 sol2);;val t2c : float 
     = 9.059906005859375e-06val sol29 : string list =  ["((25-(3+7))*(1+50))"; 
     "(((25-3)-7)*(1+50))"; …# let t2d, sol239 = time (fun () -> ltake 
     49 sol2);;val t2d : float = 4.00543212890625e-05val sol239 : string list =  
     ["((25-(3+7))*(1+50))"; "(((25-3)-7)*(1+50))"; …

     Getting elements from the list shows they are almost already computed.

   • Wait! Perhaps we should not store all candidates when we are only interested in one.

     module OptionM = MonadPlus (struct type ’a t = ’a option let bind a b =
     match a with None -> None | Some x -> b x let return a = Some a
     let mzero = None let mplus a b = match a with None -> b | Some -> aend)

   • module OptCountdown = Countdown (OptionM)let test3 () = OptionM.run (OptCountdown.solutions [1;3;7;10;25;50] 765)

   •   # let t3, sol3 = time test3;;val t3 : float = 5.0067901611328125e-06val 
       sol3 : string option = None

     It very quickly computes… nothing. Why?

     • What is the OptionM monad (Maybe monad in Haskell) good for?

   • Our lazy list type is not lazy enough.

     • Whenever we “make” a choice: a ++ b or msum_map …, it computes the first candidate for each choice path.
     • When we bind consecutive steps, it computes the second candidate of the first step even when the first candidate would suffice.

   • We want the whole monad to be lazy: it’s called even lazy lists.

     • Our llist are called odd lazy lists.

     type ’a lazylist = ’a lazylist Lazy.tand ’a lazylist = LazNil | LazCons of ’a * ’a lazylistlet rec laztake n = function | lazy (LazCons (a, l)) when n > 0 -> a::(laztake (n-1) l) | -> []let rec appendaux l1 l2 = match l1 with lazy LazNil -> Lazy.force l2 | lazy (LazCons (hd, tl)) -> LazCons (hd, lazy (appendaux tl l2))let lazappend l1 l2 = lazy (appendaux l1 l2)let rec concatmapaux f = function | lazy LazNil -> LazNil | lazy (LazCons (a, l)) -> appendaux (f a) (lazy (concatmapaux f l))let lazconcatmap f l = lazy (concatmapaux f l)

   • module LazyListM = MonadPlus (struct type ’a t = ’a lazylist let bind a b = lazconcatmap b a let return a = lazy (LazCons (a, lazy LazNil)) let mzero = lazy LazNil let mplus = lazappendend)

   • module LazyCountdown = Countdown (LazyListM)let test4 () = LazyListM.run (LazyCountdown.solutions [1;3;7;10;25;50] 765)

   •   # let t4a, sol4 = time test4;;val t4a : float = 2.86102294921875e-06val 
       sol4 : string lazylist = <lazy># let t4b, sol41 = time (fun 
       () -> laztake 1 sol4);;val t4b : float = 0.367874860763549805val sol41 : 
       string list = ["((25-(3+7))*(1+50))"]# let t4c, sol49 = time (fun () -> 
       laztake 10 sol4);;val t4c : float = 0.234670877456665039val sol49 : string 
       list =  ["((25-(3+7))*(1+50))"; "(((25-3)-7)*(1+50))"; …# let t4d, 
       sol439 = time (fun () -> laztake 49 sol4);;val t4d : float 
       = 4.0594940185546875val sol439 : string list =  ["((25-(3+7))*(1+50))"; 
       "(((25-3)-7)*(1+50))"; …

     • Finally, the first solution in considerably less time than all solutions.
     • The next 9 solutions are almost computed once the first one is.
     • But computing all solutions takes nearly twice as long as without the overhead of lazy computation.

   8.3 The exception monad

   • Built-in non-functional exceptions in OCaml are more efficient (and more flexible).
   • Instead of specifying a type of exceptional values, we could use OCaml open type exn, restoring some flexibility.
   • Monadic exceptions are safer than standard exceptions in situations like multi-threading. Monadic lightweight-thread library Lwt has throw (called fail there) and catch operations in its monad.

   module ExceptionM(Excn : sig type t end) : sig type excn = Excn.t type ’a t = OK of ’a | Bad of excn include MONADOPS val run : ’a monad -> ’a t
   val throw : excn -> ’a monad val catch : ’a monad -> (excn -> ’a monad) -> ’a monadend = struct type excn = Excn.t

   module M = struct type ’a t = OK of ’a | Bad of excn let return a = OK a let bind m b = match m with | OK a -> b a | Bad e -> Bad e end include M include MonadOps(M) let throw e = Bad e let catch m handler = match m with | OK -> m | Bad e -> handler eend

   8.4 The state monad

   module StateM(Store : sig type t end) : sig type store = Store.tPass the current store value to get the next value.type ‘a t = store -> ’a * store include MONADOPS include STATE with type ’a t := ’a monad
   and type store := store val run : ’a monad -> ’a tend = struct type store = Store.t module M = struct type ’a t = store -> ’a * store
   let return a = fun s -> a, sKeep the current value unchanged.let bind m b = fun s -> let a, s’ = m s in b a s’ endTo bind two steps, pass the value after first step to the second step. include M include MonadOps(M) let get = fun s -> s, sKeep the value unchanged but put it in monad.let put s’ = fun -> (), s’Change the value; a throwaway in monad.end

   • The state monad is useful to hide passing-around of a “current” value.

   • We will rename variables in \lambda-terms to get rid of possible name clashes.

     • This does not make a \lambda-term safe for multiple steps of \beta-reduction. Find a counter-example.

   • type term =| Var of string| Lam of string * term| App of term * term

   • let (!) x = Var xlet (|->) x t = Lam (x, t)let (@) t1 t2 = App (t1, t2)let test = “x” |-> (“x” |-> !“y” @ !“x”) @ !“x”

   • module S = StateM(struct type t = int * (string * string) list end)open S

     Without opening the module, we would write S.get, S.put and perform with S in…

   • let rec alphaconv = function | Var x as v -> performFunction from terms to StateM monad. (_, env) <– get;Seeing a variable does not change state let v = try Var (List.assoc x env)but we need its new name.
     with Notfound -> v inFree variables don’t change name. return v | Lam (x, t) -> performWe rename each bound variable. (fresh, env) <– get;We need a fresh number. let x’ = x stringofint fresh in
     put (fresh+1, (x, x’)::env);Remember new name, update number. t’ <– alphaconv t; (fresh’, ) <– get;We need to restore names, put (fresh’, env);but keep the number fresh. return (Lam (x’, t’)) | App (t1, t2) -> perform t1 <– alphaconv t1;Passing around of names
     t2 <– alphaconv t2;and the currently fresh number return (App (t1, t2))is done by the monad.

   • val test : term = Lam (“x”, App (Lam (“x”, App (Var “y”, Var “x”)), Var “x”))# let = StateM.run (alphaconv test) (5, []);;- : term * (int * (string * string) list) =(Lam (“x5”, App (Lam (“x6”, App (Var “y”, Var “x6”)), Var “x5”)), (7, []))

   • If we separated the reader monad and the state monad, we would avoid the lines: (fresh’, ) <– get;Restoring the ‘‘reader’’ part env put (fresh’, env);but preserving the ‘‘state’’ part fresh.

   • The elegant way is to define the monad locally:

     let alphaconv t = let module S = StateM (struct type t = int * (string

     • string) list end) in let open S in let rec aux = function | Var x as v -> perform (fresh, env) <– get; let v = try Var (List.assoc x env) with Notfound -> v in return v | Lam (x, t) -> perform (fresh, env) <– get; let x’ = x
       stringofint fresh in put (fresh+1, (x, x’)::env); t’ <– aux t; (fresh’, ) <– get; put (fresh’, env); return (Lam (x’, t’)) | App (t1, t2) -> perform t1 <– aux t1; t2 <– aux t2; return (App (t1, t2)) in run (aux t) (0, [])

   9 Monad transformers

   • Based on: http://lambda.jimpryor.net/monad_transformers/

   • Sometimes we need merits of multiple monads at the same time, e.g. monads AM and BM.

   • Straightforwad idea is to nest one monad within another:

     • either ’a AM.monad BM.monad
     • or ’a BM.monad AM.monad.

   • But we want a monad that has operations of both AM and BM.

   • It turns out that the straightforward approach does not lead to operations with the meaning we want.

   • A monad transformer AT takes a monad BM and turns it into a monad AT(BM) which actually wraps around BM on both sides. AT(BM) has operations of both monads.

   • We will develop a monad transformer StateT which adds state to a monad-plus. The resulting monad has all: return, bind, mzero, mplus, put, get and their supporting general-purpose functions.

     • There is no reason for StateT not to provide state to any flavor of monads. Our restriction to monad-plus is because the type/module system makes more general solutions harder.

   • We need monad transformers in OCaml because “monads are contagious”: although we have built-in state and exceptions, we need to use monadic state and exceptions when we are inside a monad.

     • The reason Lwt is both a concurrency and an exception monad.

   • Things get interesting when we have several monad transformers, e.g. AT, BT, … We can compose them in various orders: AT(BT(CM)), BT(AT(CM)), … achieving different results.

     • With a single trasformer, we will not get into issues with multiple-layer monads…
     • They are worth exploring – especially if you plan a career around programming in Haskell.

   • The state monad, using (fun x -> …) a instead of let x = a in …

     type ’a state = store -> (’a * store)

     let return (a : ’a) : ’a state = fun s -> (a, s)

     let bind (u : ‘a state) (f : ’a -> ’b state) : ’b state = fun s -> (fun (a, s’) -> f a s’) (u s)

   • Monad M transformed to add state, in pseudo-code:

     type ’a stateT(M) = store -> (’a * store) M(* notice this is not an (’a M) state *)

     let return (a : ’a) : ’a stateT(M) = fun s -> M.return (a, s)Rather than returning, M.return

     let bind(u:‘a stateT(M))(f:’a->’b stateT(M)):’b stateT(M)= fun s -> M.bind (u s) (fun (a, s’) -> f a s’)Rather than let-binding, M.bind

   9.1 State transformer

   module StateT (MP : MONADPLUSOPS) (Store : sig type t end) : sigFunctor takes two modules – the second one type store = Store.tprovides only the storage type.type ‘a t = store -> (’a * store) MP.monad include MONADPLUSOPSExporting all the monad-plus operations include STATE with type ’a t := 'a monadand state operations.and type store := store val run : ’a monad -> 'a tExpose ‘‘what happened’’ – resulting states.val runT : ’a monad -> store -> ’a MP.monadend = structRun the state transformer – get the resulting values. type store = Store.t

   module M = struct type ‘a t = store -> (’a * store) MP.monad let return a = fun s -> MP.return (a, s) let bind m b = fun s ->
   MP.bind (m s) (fun (a, s’) -> b a s’) let mzero = fun -> MP.mzeroLift the monad-plus operations.let mplus ma mb = fun s -> MP.mplus (ma s) (mb s) end include M include MonadPlusOps(M) let get = fun s -> MP.return (s, s)Instead of just returning, let put s’ = fun -> MP.return ((), s’)MP.return. let runT m s = MP.lift fst (m s)end

   9.2 Backtracking with state

   module HoneyIslands (M : MONADPLUSOPS) = struct type state = {For use with list monad or lazy list monad. beensize: int; beenislands: int;
   unvisited: cell list; visited: CellSet.t; eaten: cell list;
   moretoeat: int; } let initstate unvisited moretoeat = { beensize = 0;
   beenislands = 0; unvisited; visited = CellSet.empty; eaten = [];
   moretoeat; }

   module BacktrackingM = StateT (M) (struct type t = state end) open BacktrackingM let rec visitcell () = performState update actions. s <– get; match s.unvisited with | [] -> return None | c::remaining when CellSet.mem c s.visited -> perform put {s with unvisited=remaining}; visitcell ()Throwaway argument because of recursion. See () | c::remaining ( when c not visited *) -> perform put {s with unvisited=remaining; visited = CellSet.add c s.visited}; return (Some c)This action returns a value.

   let eatcell c = perform s <– get; put {s with eaten = c::s.eaten; visited = CellSet.add c s.visited; moretoeat = s.moretoeat - 1}; return ()Remaining state update actions just affect the state. let keepcell c = perform s <– get; put {s with
   visited = CellSet.add c s.visited; beensize = s.beensize + 1};
   return () let freshisland = perform s <– get; put {s with beensize = 0; beenislands = s.beenislands + 1}; return ()

   let findtoeat n islandsize numislands emptycells = let honey = honeycells n emptycells inOCaml does not realize that 'a monad with state is actually a function – let rec findboard () = performit’s an abstract type.(*)
   cell <– visitcell (); match cell with | None -> perform s <– get; guard (s.beenislands = numislands); return s.eaten | Some cell -> perform
   freshisland; findisland cell; s <– get;
   guard (s.beensize = islandsize); findboard ()

   and findisland current = perform        keepcell current;        neighbors 

   n emptycells current |> foldMThe partial answer sits in the state – throwaway result.(fun () neighbor -> perform s <– get; whenM (not (CellSet.mem neighbor s.visited))
   (let chooseeat = perform guard (s.moretoeat > 0); eatcell neighbor
   and choosekeep = perform guard (s.beensize < islandsize); findisland neighbor in
   chooseeat ++ choosekeep)) () in

   let cellstoeat =      List.length honey - islandsize * numislands in    

   initstate honey cellstoeat |> runT (findboard ())endmodule HoneyL = HoneyIslands (ListM)let findtoeat a b c d = ListM.run (HoneyL.findtoeat a b c d)

   10 Probabilistic Programming

   • Using a random number generator, we can define procedures that produce various output. This is not functional – mathematical functions have a deterministic result for fixed arguments.
   • Similarly to how we can “simulate” (mutable) variables with state monad and non-determinism (i.e. making choices) with list monad, we can “simulate” random computation with probability monad.
   • The probability monad class means much more than having randomized computation. We can ask questions about probabilities of results. Monad instances can make tradeoffs of efficiency vs. accuracy (exact vs.  approximate probabilities).
   • Probability monad imposes limitations on what approximation algorithms can be implemented.
     • Efficient probabilistic programming library for OCaml, based on continuations, memoisation and reified search trees:http://okmij.org/ftp/kakuritu/index.html

   10.1 The probability monad

   • The essential functions for the probability monad class are choose and distrib – remaining functions could be defined in terms of these but are provided by each instance for efficiency.

   • Inside-monad operations:

     • choose : float -> ’a monad -> ’a monad -> ’a monad

       choose p a b represents an event or distribution which is a with probability p and is b with probability 1 - p.

     • val pick : (’a * float) list -> ’a t

       A result from the provided distribution over values. The argument must be a probability distribution: positive values summing to 1.

     • val uniform : ’a list -> ’a monad

       Uniform distribution over given values.

     • val flip : float -> bool monad

       Equal to choose 0.5 (return true) (return false).

     • val coin : bool monadEqual to flip 0.5.

   • And some operations for getting out of the monad:

     • val prob : (’a -> bool) -> ’a monad -> float

       Returns the probability that the predicate holds.

     • val distrib : ’a monad -> (’a * float) list

       Returns the distribution of probabilities over the resulting values.

     • val access : ’a monad -> ’a

       Samples a random result from the distribution – non-functional behavior.

   • We give two instances of the probability monad: exact distribution monad, and sampling monad, which can approximate distributions.

     • The sampling monad is entirely non-functional: in Haskell, it lives in the IO monad.

   • The monad instances indeed represent probability distributions: collections of positive numbers that add up to 1 – although often merge rather than normalize is used. If pick and choose are used correctly.

   • module type PROBABILITY = sigProbability monad class. include MONADOPS val choose : float -> ’a monad -> ’a monad -> ’a monad val pick : (’a * float) list -> 'a monad val uniform : ’a list -> ’a monadval coin : bool monad val flip : float -> bool monad val prob : (’a -> bool) -> ’a monad -> float val distrib : ’a monad -> (’a * float) list val access : ’a monad -> ’aend

   • let total dist =Helper functions. List.foldleft (fun a (,b)->a+.b) 0. distlet merge dist =Merge repeating elements. mapreduce (fun x->x) (+.) 0. distlet normalize dist = Normalize a measure into a distribution.
     let tot = total dist in if tot = 0. then dist else List.map (fun (e,w)->e,w/.tot) distlet roulette dist =Roulette wheel from a distribution/measure. let tot = total dist in let rec aux r = function [] -> assert false | (e,w):: when w <= r -> e | (,w)::tl -> aux (r-.w) tl in aux (Random.float tot) dist

   • module DistribM : PROBABILITY = struct module M = structExact probability distribution – naive implementation. type ’a t = (’a * float) list
     let bind a b = merge``x w.p. p and then y w.p. q happens =[y, q*.p | (x,p) <- a; (y,q) <- b x]y results w.p. p q. let return a = [a, 1.]Certainly a. end include M include MonadOps (M) let choose p a b = List.map (fun (e,w) -> e, p.w) a @ List.map (fun (e,w) -> e, (1. -.p).w) b let pick dist = dist let uniform elems = normalize (List.map (fun e->e,1.) elems)let coin = [true, 0.5; false, 0.5] let flip p = [true, p; false, 1. -. p]

     let prob p m = m |> List.filter (fun (e,) -> p e)All cases where p holds, |> List.map snd |> List.foldleft (+.) 0.add up.
     let distrib m = m let access m = roulette mend

   • module SamplingM (S : sig val samples : int end) : PROBABILITY = structParameterized by how many samples module M = structused to approximate prob or distrib. type ’a t = unit -> 'aRandomized computation – each call a()let bind a b () = b (a ()) () is an independent sample. let return a = fun () -> aAlways a.end include M include MonadOps (M) let choose p a b () = if Random.float 1. <= p then a () else b () let pick dist = fun () -> roulette dist let uniform elems = let n = List.length elems in fun () -> List.nth (Random.int n) elemslet coin = Random.bool let flip p = choose p (return true) (return false)

     let prob p m = let count = ref 0 in for i = 1 to S.samples do
     if p (m ()) then incr count done; floatofint !count /. floatofint S.sampleslet distrib m = let dist = ref [] in for i = 1 to S.samples do dist := (m (), 1.) :: !dist done; normalize (merge !dist) let access m = m ()end

   10.2 Example: The Monty Hall problem

   • http://en.wikipedia.org/wiki/Monty_Hall_problem: > In search of a new car, the player picks a door, say 1. The game host > then opens one of the other doors, say 3, to reveal a goat and offers to > let the player pick door 2 instead of door 1.

   • module MontyHall (P : PROBABILITY) = struct open P type door = A | B | C
     let doors = [A; B; C]

     let montywin switch = perform prize <– uniform doors;
     chosen <– uniform doors; opened <– uniform (listdiff doors [prize; chosen]); let final = if switch then List.hd
     (listdiff doors [opened; chosen]) else chosen in return (final = prize)end

   • module MontyExact = MontyHall (DistribM)module Sampling1000 = SamplingM (struct let samples = 1000 end)module MontySimul = MontyHall (Sampling1000)

   •   # let t1 = DistribM.distrib (MontyExact.montywin false);;val t1 : (bool * 
       float) list =  [(true, 0.333333333333333315); (false, 0.66666666666666663)]# 
       let t2 = DistribM.distrib (MontyExact.montywin true);;val t2 : (bool * 
       float) list =  [(true, 0.66666666666666663); (false, 0.333333333333333315)]# 
       let t3 = Sampling1000.distrib (MontySimul.montywin false);;val t3 : (bool * 
       float) list = [(true, 0.313); (false, 0.687)]# let t4 = Sampling1000.distrib 
       (MontySimul.montywin true);;val t4 : (bool * float) list = [(true, 0.655); 
       (false, 0.345)]

     10.3 Conditional probabilities

   • Wouldn’t it be nice to have a monad-plus rather than a monad?

   • We could use guard – conditional probabilities!

     • P (A|B)
       • Compute what is needed for both A and B.
       • Guard B.
       • Return A.

   • For the exact distribution monad it turns out very easy – we just need to allow intermediate distributions to be unnormalized (sum to less than 1).

   • For the sampling monad we use rejection sampling.

     • mplus has no straightforward correct implementation.

   • We implemented PROBABILITY separately for educational purposes only, as COND_PROBAB introduced below supersedes it.

   • module type CONDPROBAB = sigClass for conditional probability monad,
     include PROBABILITYwhere guard cond conditions on cond. include MONADPLUSOPS with type ’a monad := ’a monadend

   • module DistribMP : CONDPROBAB = struct module MP = structThe measures no longer restricted to type ’a t = (’a * float) listprobability distributions: let bind a b = merge [y, q*.p | (x,p) <- a; (y,q) <- b x] let return a = [a, 1.] let mzero = []Measure equal 0 everywhere is OK. let mplus = List.append end include MP include MonadPlusOps (MP) let choose p a b =It isn’t a w.p. p & b w.p. (1 - p) since a and b List.map (fun (e,w) -> e, p.w) a @are not normalized!List.map (fun (e,w) -> e, (1. -.p).w) b let pick dist = dist

     let uniform elems = normalize (List.map (fun e->e,1.) elems) let coin = [true, 0.5; false, 0.5] let flip p = [true, p; false, 1. -. p] let prob p m = normalize mFinal normalization step.|> List.filter (fun (e,) -> p e) |> List.map snd |> List.foldleft (+.) 0. let distrib m = normalize m let access m = roulette mend

   • We write the rejection sampler in mostly imperative style:

     module SamplingMP (S : sig val samples : int end) : CONDPROBAB = struct
     exception RejectedFor rejecting current sample. module MP = structMonad operations are exactly as for SamplingM type ’a t = unit -> ’a let bind a b () = b (a ()) () let return a = fun () -> a let mzero = fun () -> raise Rejectedbut now we can fail. let mplus a b = fun () -> failwith “SamplingMP.mplus not implemented” end include MP include MonadPlusOps (MP)

     let choose p a b () =Inside-monad operations don’t change. if Random.float 1. <= p then a () else b () let pick dist = fun () -> roulette distlet uniform elems = let n = List.length elems in fun () -> List.nth elems (Random.int n) let coin = Random.bool let flip p = choose p (return true) (return false)

     let prob p m =Getting out of monad: handle rejected samples. let count = ref 0 and tot = ref 0 in while !tot < S.samples doCount up to the required trynumber of samples. if p (m ()) then incr count;m() can fail. incr totBut if we got here it hasn’t.with Rejected -> ()Rejected, keep sampling. done; floatofint !count /. floatofint S.samples

     let distrib m = let dist = ref [] and tot = ref 0 in while !tot < S.samples do try dist := (m (), 1.) :: !dist; incr tot
     with Rejected -> () done; normalize (merge !dist) let rec access m = try m () with Rejected -> access mend

   10.4 Burglary example: encoding a Bayes net

   • We’re faced with a problem with the following dependency structure:

     	Burglary				Earthquake
     			Alarm
     	John calls				Mary calls

     -5.525383.15826-3.04886559068663.17942188120122-3.133532874718882.73491864003175-2.11753-0.376604-0.297178859637518-0.418937690170658-0.318345680645588-0.228436301098029-5.82172-4.9063-2.98536512766239-4.90630374388147-3.64153657891255-6.028145257309170.570661-4.863973.63984984786347-4.906303743881472.85667747056489-6.091645720333380.7399953.158263.682183489879613.094754597168943.512848921815052.50208360894298-3.346952.3791-1.790454363947570.2764614914471450.9764792.39298-0.6819827901385850.319857839429467-1.87545-1.04339-3.6026998120943-3.65669671517365-0.55984-1.063621.16004444583979-3.529329161908520cm

     • Alarm can be due to either a burglary or an earthquake.
     • I’ve left on vacations.
     • I’ve asked neighbors John and Mary to call me if the alarm rings.
     • Mary only calls when she is really sure about the alarm, but John has better hearing.
     • Earthquakes are twice as probable as burglaries.
     • The alarm has about 30% chance of going off during earthquake.
     • I can check on the radio if there was an earthquake, but I might miss the news.

   • module Burglary (P : CONDPROBAB) = struct open P type whathappened =
     Safe | Burgl | Earthq | Burglnearthq

     let check \simjohncalled \simmarycalled \simradio = perform
     earthquake <– flip 0.002; guard (radio = None || radio = Some earthquake); burglary <– flip 0.001; let alarmp = match burglary, earthquake with | false, false -> 0.001 | false, true -> 0.29 | true, false -> 0.94 | true, true -> 0.95 in alarm <– flip alarmp;

     let johnp = if alarm then 0.9 else 0.05 in    johncalls <-- flip 

     johnp; guard (johncalls = johncalled); let maryp = if alarm then 0.7 else 0.01 in marycalls <– flip maryp; guard (marycalls = marycalled); match burglary, earthquake with | false, false -> return Safe | true, false -> return Burgl | false, true -> return Earthq | true, true -> return Burglnearthqend

   • module BurglaryExact = Burglary (DistribMP)module Sampling2000 = SamplingMP (struct let samples = 2000 end)module BurglarySimul = Burglary (Sampling2000)

   # let t1 = DistribMP.distrib  (BurglaryExact.check $\sim$johncalled:true 
   $\sim$marycalled:false     $\sim$radio:None);;    val t1 : 
   (BurglaryExact.whathappened * float) list =  
   [(BurglaryExact.Burglnearthq, 1.03476433660005444e-05);   
   (BurglaryExact.Earthq, 0.00452829235738691407);   
   (BurglaryExact.Burgl, 0.00511951049003530299);   
   (BurglaryExact.Safe, 0.99034184950921178)]# let t2 = DistribMP.distrib  
   (BurglaryExact.check $\sim$johncalled:true $\sim$marycalled:true     
   $\sim$radio:None);;    val t2 : (BurglaryExact.whathappened * float) list =  
   [(BurglaryExact.Burglnearthq, 0.00057437256500405794);   
   (BurglaryExact.Earthq, 0.175492465840075218);   
   (BurglaryExact.Burgl, 0.283597462799388911);   
   (BurglaryExact.Safe, 0.540335698795532)]# let t3 = DistribMP.distrib  
   (BurglaryExact.check $\sim$johncalled:true $\sim$marycalled:true     
   $\sim$radio:(Some true));;    val t3 : (BurglaryExact.whathappened * float) 
   list =  [(BurglaryExact.Burglnearthq, 0.0032622416021499262);   
   (BurglaryExact.Earthq, 0.99673775839785006)]
   
   # let t4 = Sampling2000.distrib  (BurglarySimul.check $\sim$johncalled:true 
   $\sim$marycalled:false     $\sim$radio:None);;    val t4 : 
   (BurglarySimul.whathappened * float) list =  [(BurglarySimul.Earthq, 0.0035); 
   (BurglarySimul.Burgl, 0.0035);   (BurglarySimul.Safe, 0.993)]# let t5 = 
   Sampling2000.distrib  (BurglarySimul.check $\sim$johncalled:true 
   $\sim$marycalled:true     $\sim$radio:None);;    val t5 : 
   (BurglarySimul.whathappened * float) list =  
   [(BurglarySimul.Burglnearthq, 0.0005); (BurglarySimul.Earthq, 0.1715);   
   (BurglarySimul.Burgl, 0.2875); (BurglarySimul.Safe, 0.5405)]# let t6 = 
   Sampling2000.distrib  (BurglarySimul.check $\sim$johncalled:true 
   $\sim$marycalled:true     $\sim$radio:(Some true));;    val t6 : 
   (BurglarySimul.whathappened * float) list =  
   [(BurglarySimul.Burglnearthq, 0.0015); (BurglarySimul.Earthq, 0.9985)]

   11 Lightweight cooperative threads

   • bind is inherently sequential: bind a (fun x -> b) computes a, and resumes computing b only once the result x is known.

   • For concurrency we need to “suppress” this sequentiality. We introduce

     parallel :’a monad-> ’b monad-> (’a -> ’b -> ’c monad) -> ’c monad

     where parallel a b (fun x y -> c) does not wait for a to be computed before it can start computing b.

   • It can be that only accessing the value in the monad triggers the computation of the value, as we’ve seen in some monads.

     • The state monad does not start computing until you “get out of the monad” and pass the initial value.
     • The list monad computes right away – the 'a monad value is the computed results.

     In former case, a “built-in” parallel is necessary for concurrency.

   • If the monad starts computing right away, as in the Lwt library, parallel \concat{e}{\rsub{a}} \concat{e}{\rsub{b}} c is equivalent to

     perform let a = e_{a} in let b = e_{b} in x <– a; y <– b; c x y

     • We will follow this model, with an imperative implementation.
     • In any case, do not call run or access from within a monad.

   • We still need to decide on when concurrency happens.

     • Under fine-grained concurrency, every bind is suspended and computation moves to other threads.
       • It comes back to complete the bind before running threads created since the bind was suspended.
       • We implement this model in our example.
     • Under coarse-grained concurrency, computation is only suspended when requested.
       • Operation suspend is often called yield but the meaning is more similar to Await than Yield from lecture 7.
       • Library operations that need to wait for an event or completion of IO (file operations, etc.) should call suspend or its equivalent internally.
       • We leave coarse-grained concurrency as exercise 11.

   • The basic operations of a multithreading monad class.

     module type THREADS = sig include MONAD val parallel : ’a t -> ’b t -> (’a -> ’b -> ’c t) -> ’c tend

   • Although in our implementation parallel will be redundant, it is a principled way to make sure subthreads of a thread are run concurrently.

   • All within-monad operations.

     module type THREADOPS = sig include MONADOPS include THREADS with type ’a t := ’a monad val parallelmap : ’a list -> (’a -> ’b monad) -> ’b list monad val (>||=) : ’a monad -> ’b monad -> (’a -> ’b -> ’c monad) -> ’c monad val (>||) : ’a monad -> ’b monad -> (unit -> ’c monad) -> ’c monadend

   • Outside-monad operations.

     module type THREADSYS = sig include THREADS val access : ’a t -> ’a
     val killthreads : unit -> unitend

   • Helper functions.

     module ThreadOps (M : THREADS) = struct open M include MonadOps (M) let parallelmap l f = List.foldright (fun a bs -> parallel (f a) bs
     (fun a bs -> return (a::bs))) l (return []) let (>||=) = parallel let (>||) a b c = parallel a b (fun -> c ())end

   • Put an interface around an implementation.

     module Threads (M : THREADSYS) :sig include THREADOPS val access : ’a monad -> ’a val killthreads : unit -> unitend = struct include M
     include ThreadOps(M)end

   • Our implementation, following the Lwt paper.

   module Cooperative = Threads(struct type ‘a state = | Return of 'aThe thread has returned.| Sleep of (’a -> unit) listWhen thread returns, wake up waiters.| Link of 'a tA link to the actual thread.and ’a t = {mutable state : ’a state}State of the thread can change– it can return, or more waiters can be added.let rec find t = match t.state withUnion-find style link chasing. | Link t -> find t | -> t let jobs = Queue.create ()Work queue – will storeunit -> unit procedures. let wakeup m a =Thread m has actually finished – let m = find m inupdating its state. match m.state with | Return -> assert false | Sleep waiters -> m.state <- Return a;Set the state, and only then
   List.iter ((|>) a) waiterswake up the waiters. | Link -> assert false let return a = {state = Return a}let connect t t’ =t was a placeholder for t'. let t’ = find t’ in match t’.state with | Sleep waiters’ -> let t = find t in (match t.state with | Sleep waiters ->If both sleep, collect their waiters t.state <- Sleep (waiters’ @ waiters); t’.state <- Link tand link one to the other.| -> assert false) | Return x -> wakeup t xIf t' returned, wake up the placeholder.| Link -> assert falselet rec bind a b = let a = find a in let m = {state = Sleep []} inThe resulting monad.
   (match a.state with | Return x ->If a returned, we suspend further work. let job () = connect m (b x) in(In exercise 11, this should
   Queue.push job jobsonly happen after suspend.)| Sleep waiters ->If a sleeps, we wait for it to return. let job x = connect m (b x) in
   a.state <- Sleep (job::waiters) | Link -> assert false); m
   let parallel a b c = performSince in our implementation x <– a;the threads run as soon as they are created, y <– b;parallel is redundant. c x ylet rec access m =Accessing not only gets the result of m, let m = find m inbut spins the thread loop till m terminates. match m.state with | Return x -> xNo further work.| Sleep -> (try Queue.pop jobs ()Perform suspended work. with Queue.Empty ->
   failwith “access: result not available”); access m | Link -> assert false let killthreads () = Queue.clear jobsRemove pending work.end)

   • module TTest (T : THREADOPS) = struct open T let rec loop s n = perform
     return (Printf.printf “– %s(%d)%!” s n); if n > 0 then loop s (n-1)We cannot use whenM because else return ()the thread would be created regardless of condition.endmodule TT = TTest (Cooperative)
   • let test = Cooperative.killthreads ();Clean-up after previous tests. let thread1 = TT.loop “A” 5 in let thread2 = TT.loop “B” 4 in
     Cooperative.access thread1;We ensure threads finish computing
     Cooperative.access thread2before we proceed.

   # let test =    Cooperative.killthreads ();    let thread1 = TT.loop "A" 5 in    let thread2 = TT.loop "B" 4 in    Cooperative.access thread1;    Cooperative.access thread2;;-- A(5)-- B(4)-- A(4)-- B(3)-- A(3)-- B(2)-- A(2)-- B(1)-- A(1)-- B(0)-- A(0)val test : unit = ()

   Exercise 1.

   Puzzle via Oleg Kiselyov.

   “U2” has a concert that starts in 17 minutes and they must all cross a bridge to get there. All four men begin on the same side of the bridge. It is night. There is one flashlight. A maximum of two people can cross at one time. Any party who crosses, either 1 or 2 people, must have the flashlight with them. The flashlight must be walked back and forth, it cannot be thrown, etc.. Each band member walks at a different speed. A pair must walk together at the rate of the slower man’s pace:

   • Bono: 1 minute to cross
   • Edge: 2 minutes to cross
   • Adam: 5 minutes to cross
   • Larry: 10 minutes to cross

   For example: if Bono and Larry walk across first, 10 minutes have elapsed when they get to the other side of the bridge. If Larry then returns with the flashlight, a total of 20 minutes have passed and you have failed the mission.

   Find all answers to the puzzle using a list comprehension. The comprehension will be a bit long but recursion is not needed.

   Exercise 2.

   Assume concat_map as defined in lecture 6. What will the following expresions return? Why?

   1. perform with (|->) in return 5; return 7
   2. let guard p = if p then [()] else [];;perform with (|->) in guard false; return 7;;
   3. perform with (|->) in return 5; guard false; return 7;;

   Exercise 3.

   Define bind in terms of lift and join.

   Exercise 4.

   Define a monad-plus implementation based on binary trees, with constant-time mzero and mplus. Starter code:type ’a tree = Empty | Leaf of ’a | T of ’a t * ’a tmodule TreeM = MonadPlus (struct type ’a t = ’a tree let bind a b = TODO let return a = TODO let mzero = TODO let mplus a b = TODOend)

   Exercise 5.

   Show the monad-plus laws for one of:

   1. TreeM from your solution of exercise ;
   2. ListM from lecture.

   Exercise 6.

   Why the following monad-plus is not lazy enough?

   • let rec badappend l1 l2 = match l1 with lazy LazNil -> l2 | lazy (LazCons (hd, tl)) -> lazy (LazCons (hd, badappend tl l2))let rec badconcatmap f = function | lazy LazNil -> lazy LazNil | lazy (LazCons (a, l)) -> badappend (f a) (badconcatmap f l)
   • module BadyListM = MonadPlus (struct type ’a t = ’a lazylist let bind a b = badconcatmap b a let return a = lazy (LazCons (a, lazy LazNil)) let mzero = lazy LazNil let mplus = badappendend)
   • module BadyCountdown = Countdown (BadyListM)let test5 () = BadyListM.run (BadyCountdown.solutions [1;3;7;10;25;50] 765)

   • let t5a, sol5 = time test5;;val t5a : float = 3.3954310417175293val sol5 :

     string lazylist = # let t5b, sol51 = time (fun () -> laztake 1 sol5);;val t5b : float = 3.0994415283203125e-06val sol51 : string list = [“((25-(3+7))*(1+50))”]# let t5c, sol59 = time (fun () -> laztake 10 sol5);;val t5c : float = 7.8678131103515625e-06val sol59 : string list = [“((25-(3+7))*(1+50))”; “(((25-3)-7)*(1+50))”; …# let t5d, sol539 = time (fun () -> laztake 49 sol5);;val t5d : float = 2.59876251220703125e-05val sol539 : string list =
     [“((25-(3+7))*(1+50))”; “(((25-3)-7)*(1+50))”; …

   Exercise 7.

   Convert a “rectangular” list of lists of strings, representing a matrix with inner lists being rows, into a string, where elements are column-aligned. (Exercise not related to recent material.)

   Exercise 8.

   Recall the overly rich way to introduce monads – providing the freedom of additional parametermodule type MONAD = sig type (’s, ’a) t val return : ’a -> (’s, ’a) t val bind : (’s, ’a) t -> (’a -> (’s, ’b) t) -> (’s, ’b) tend

   Recall the operations for the exception monad:val throw : excn -> ’a monadval catch : ’a monad -> (excn -> ’a monad) -> ’a monad

   1. Design the signatures for the exception monad operations to use the enriched monads with (’s, ’a) monad type, so that they provide more flexibility than our exception monad.
   2. Does the implementation of the exception monad need to change? The same implementation can work with both sets of signatures, but the implementation given in lecture needs a very slight change. Can you find it without implementing? If not, the lecture script provides RMONAD, RMONAD_OPS, RMonadOps and RMonad, so you can implement and see for yourself – copy ExceptionM and modify:module ExceptionRM : sig type (’e, ’a) t = KEEP/TODO include RMONADOPS val run : (’e, ’a) monad -> (’e, ’a) t val throw : TODO val catch : TODOend = struct module M = struct
      type (’e, ’a) t = KEEP/TODO let return a = OK a let bind m b = KEEP/TODO end include M include RMonadOps(M) let throw e = KEEP/TODO
      let catch m handler = KEEP/TODOend

   Exercise 9.

   Implement the following constructs for all monads:

   1. for…to…
   2. for…downto…
   3. while…do…
   4. do…while…
   5. repeat…until…

   Explain how, when your implementation is instantiated with the StateM monad, we get the solution to exercise 2 from lecture 4.

   Exercise 10.

   A canonical example of a probabilistic model is that of a lawn whose grass may be wet because it rained, because the sprinkler was on, or for some other reason. Oleg Kiselyov builds on this example with variables rain, sprinkler, and wet_grass, by adding variables cloudy and wet_roof. The probability tables are:

   \begin{eqnarray*} P (\operatorname{cloudy}) & = & 0.5 \\\\\\ P (\operatorname{rain}|\operatorname{cloudy}) & = & 0.8 \\\\\\ P (\operatorname{rain}|\operatorname{not}\operatorname{cloudy}) & = & 0.2 \\\\\\ P (\operatorname{sprinkler}|\operatorname{cloudy}) & = & 0.1 \\\\\\ P (\operatorname{sprinkler}|\operatorname{not}\operatorname{cloudy}) & = & \0.5 \\\\\\ P (\operatorname{wet}\operatorname{roof}|\operatorname{not}\operatorname{rain}) & = & 0 \\\\\\ P (\operatorname{wet}\operatorname{roof}|\operatorname{rain}) & = & 0.7 \\\\\\ P (\operatorname{wet}\operatorname{grass}|\operatorname{rain} \wedge \operatorname{not}\operatorname{sprinkler}) & = & 0.9 \\\\\\ P (\operatorname{wet}\operatorname{grass}|\operatorname{sprinkler} \wedge \operatorname{not}\operatorname{rain}) & = & 0.9 \end{eqnarray*}

   We observe whether the grass is wet and whether the roof is wet. What is the probability that it rained?

   Exercise 11.

   Implement the coarse-grained concurrency model.

   • Modify bind to compute the resulting monad straight away if the input monad has returned.
   • Introduce suspend to do what in the fine-grained model was the effect of bind (return a) b, i.e. suspend the work although it could already be started.
   • One possibility is to introduce suspend of type unit monad, introduce a “dummy” monadic value Suspend (besides Return and Sleep), and define bind suspend b to do what bind (return ()) b would formerly do.

   Lecture 9: Compiler

   Compilation. Runtime. Optimization. Parsing.

   Andrew W. Appel ‘‘Modern Compiler Implementation in ML’‘E. Chailloux, P. Manoury, B. Pagano ‘‘Developing Applications with OCaml’‘Jon D. Harrop ‘‘OCaml for Scientists’’Francois Pottier, Yann Regis-Gianas ‘‘Menhir Reference Manual’’

   If you see any error on the slides, let me know!

   1 OCaml Compilers

   • OCaml has two primary compilers: the bytecode compiler ocamlc and the native code compiler ocamlopt.

     • Natively compiled code runs about 10 times faster than bytecode – depending on program.

   • OCaml has an interactive shell called toplevel (in other languages, repl): ocaml which is based on the bytecode compiler.

     • There is a toplevel ocamlnat based on the native code compiler but currently not part of the binary distribution.

   • There are “third-party” compilers, most notably js_of_ocaml which translates OCaml bytecode into JavaScript source.

     • On modern JS virtual machines like V8 the result can be 2-3x faster than on OCaml virtual machine (but can also be slower).

   • Stages of compilation:

   • Programs:

     ocaml	toplevel loop
     ocamlrun	bytecode interpreter (VM)
     camlp4	preprocessor (syntax extensions)
     ocamlc	bytecode compiler
     ocamlopt	native code compiler
     ocamlmktop	new toplevel constructor
     ocamldep	dependencies between modules
     ocamlbuild	building projects tool
     ocamlbrowser	graphical browsing of sources

   • File extensions:

     .ml	OCaml source file
     .mli	OCaml interface source file
     .cmi	compiled interface
     .cmo	bytecode-compiled file
     .cmx	native-code-compiled file
     .cma	bytecode-compiled library (several source files)
     .cmxa	native-code-compiled library
     .cmt/.cmti/.annot	type information for editors
     .c	C source file
     .o	C native-code-compiled file
     .a	C native-code-compiled library

   • Both compilers commands:

     -a	construct a runtime library
     -c	compile without linking
     -o	name_of_executable specify the name of the executable
     -linkall	link with all libraries used
     -i	display all compiled global declarations
     -pp	command uses command as preprocessor
     -unsafe	turn off index checking for arrays
     -v	display the version of the compiler
     -w list	choose among the list the level of warning message
     -impl file	indicate that file is a Caml source (.ml)
     -intf file	indicate that file is a Caml interface (.mli)
     -I directory	add directory in the list of directories; prefix + for relative
     -g	generate debugging information

   • Warning levels:

     A/a	enable/disable all messages
     F/f	partial application in a sequence
     P/p	for incomplete pattern matching
     U/u	for missing cases in pattern matching
     X/x	enable/disable all other messages for hidden object
     M/m, V/v	object-oriented related warnings

   • Native compiler commands:

     -compact	optimize the produced code for space
     -S	keeps the assembly code in a file
     -inline	level set the aggressiveness of inlining

   • Environment variable OCAMLRUNPARAM:

     b	print detailed stack backtrace of runtime exceptions
     s/h/i	size of the minor heap/major heap/size increment
     o/O	major GC speed setting / heap compaction trigger setting

     Typical use, running prog: export OCAMLRUNPARAM='b'; ./prog

     To have stack backtraces, compile with option -g.

   • Toplevel loop directives:

     #quit;;	exit
     #directory "dir";;	add dir to the “search path”; + for rel.
     #cd "dir-name";;	change directory
     #load "file-name";;	load a bytecode .cmo/.cma file
     #load_rec "file-name";;	load the files file-name depends on too
     #use "file-name";;	read, compile and execute source phrases
     #instal_printer pr_nm;;	register pr_nm to print values of a type
     #print_depth num;;	how many nestings to print
     #print_length num;;	how many nodes to print – the rest …
     #trace func;;/#untrace	trace calls to func/stop tracing

   1.1 Compiling multiple-file projects

   • Traditionally the file containing a module would have a lowercase name, although the module name is always uppercase.

     • Some people think it is more elegant to use uppercase for file names, to reflect module names, i.e. for MyModule, use MyModule.ml rather than myModule.ml.

   • We have a project with main module main.ml and helper modules sub1.ml and sub2.ml with corresponding interfaces.

   • Native compilation by hand:

     …:…/Lec9$ ocamlopt sub1.mli…:…/Lec9$ ocamlopt sub2.mli…:…/Lec9$ ocamlopt -c sub1.ml…:…/Lec9$ ocamlopt -c sub2.ml…:…/Lec9$ ocamlopt -c main.ml…:…/Lec9$ ocamlopt unix.cmxa sub1.cmx sub2.cmx main.cmx -o prog…:…/Lec9$ ./prog

   • Native compilation using make:

   PROG := prog
   LIBS := unix
   SOURCES := sub1.ml sub2.ml main.ml
   INTERFACES := $(wildcard *.mli)
   OBJS := $(patsubst %.ml,%.cmx,$(SOURCES))
   LIBS := $(patsubst %,%.cmxa,$(LIBS))
   $(PROG): $(OBJS)
   ocamlopt -o $@ $(LIBS) $(OBJS)
   clean: rm -rf $(PROG) *.o *.cmx *.cmi *~
   %.cmx: %.ml
   ocamlopt -c $*.ml
   %.cmi: %.mli
   ocamlopt -c $*.mli
   depend: $(SOURCES) $(INTERFACES)
   ocamldep -native $(SOURCES) $(INTERFACES)

   • First use command: touch .depend; make depend; make
   • Later just make, after creating new source files make depend
   • Using ocamlbuild

     • files with compiled code are created in _build directory

     • Command: ocamlbuild -libs unix main.native

     • Resulting program is called main.native (in directory _build, but with a link in the project directory)

     • More arguments passed after comma, e.g.

       ocamlbuild -libs nums,unix,graphics main.native

     • Passing parameters to the compiler with -cflags, e.g.:

       ocamlbuild -cflags -I,+lablgtk,-rectypes hello.native

     • Adding a – at the end (followed with command-line arguments for the program) will compile and run the program:

       ocamlbuild -libs unix main.native --

   1.2 Editors

   • Emacs
     • ocaml-mode from the standard distribution
     • alternative tuareg-mode https://forge.ocamlcore.org/projects/tuareg/
       • cheat-sheet: http://www.ocamlpro.com/files/tuareg-mode.pdf
     • camldebug intergration with debugger
     • type feedback with C-c C-t key shortcut, needs .annot files
   • Vim
     • OMLet plugin http://www.lix.polytechnique.fr/~dbaelde/productions/omlet.html
     • For type lookup: either https://github.com/avsm/ocaml-annot
       • or http://www.vim.org/scripts/script.php?script_id=2025
       • also? http://www.vim.org/scripts/script.php?script_id=1197
   • Eclipse
     • OCaml Development Tools http://ocamldt.free.fr/
     • an old plugin OcaIDE http://www.algo-prog.info/ocaide/
   • TypeRex http://www.typerex.org/
     • currently mostly as typerex-mode for Emacs but integration with other editors will become better
     • Auto-completion of identifiers (experimental)
     • Browsing of identifiers: show type and comment, go to definition
     • local and whole-program refactoring: renaming identifiers and compilation units, open elimination
   • Indentation tool ocp-ident https://github.com/OCamlPro/ocp-indent
     • Installation instructions for Emacs and Vim
     • Can be used with other editors.
   • Some dedicated editors
     • OCamlEditor http://ocamleditor.forge.ocamlcore.org/
     • ocamlbrowser inspects libraries and programs
       • browsing contents of modules
       • search by name and by type
       • basic editing, with syntax highlighting
     • Cameleon http://home.gna.org/cameleon/ (older)
     • Camelia http://camelia.sourceforge.net/ (even older)

   2 Imperative features in OCaml

   OCaml is not a purely functional language, it has built-in:

   • Mutable arrays.

     let a = Array.make 5 0 ina.(3) <- 7; a.(2), a.(3)

     • Hashtables in the standard distribution (based on arrays).

       let h = Hashtbl.create 11 inTakes initial size of the array.Hashtbl.add h “Alpha” 5; Hashtbl.find h “Alpha”

   • Mutable strings. (Historical reasons…)

     let a = String.make 4 ‘a’ ina.[2] <- ‘b’; a.[2], a.[3]

     • Extensible mutable strings Buffer.t in standard distribution.

   • Loops:

     • for i = a to/downto b do body done
     • while condition do body done

   • Mutable record fields, for example:

     type ’a ref = { mutable contents : ’a }Single, mutable field.

     A record can have both mutable and immutable fields.

     • Modifying the field: record.field <- new_value

     • The ref type has operations:

       let (:=) r v = r.contents <- vlet (!) r = r.contents

   • Exceptions, defined by exception, raised by raise and caught by try-with clauses.

     • An exception is a variant of type exception, which is the only open algebraic datatype – new variants can be added to it.

   • Input-output functions have no “type safeguards” (no IO monad).

   Using global state e.g. reference cells makes code non re-entrant: finish one task before starting another – any form of concurrency is excluded.

   2.1 Parsing command-line arguments

   To go beyond Sys.argv array, see Arg module:http://caml.inria.fr/pub/docs/manual-ocaml/libref/Arg.html

   type config = { Example: configuring a Mine Sweeper game. nbcols : int ; nbrows : int ; nbmines : int }let defaultconfig = { nbcols=10; nbrows=10; nbmines=15 }let setnbcols cf n = cf := {!cf with nbcols = n}let setnbrows cf n = cf := {!cf with nbrows = n}let setnbmines cf n = cf := {!cf with nbmines = n}let readargs() = let cf = ref defaultconfig inState of configuration let speclist = will be updated by given functions. [(“-col”, Arg.Int (setnbcols cf), “number of columns”); (“-lin”, Arg.Int (setnbrows cf), “number of lines”); (“-min”, Arg.Int (setnbmines cf), “number of mines”)] in let usagemsg = “usage : minesweep [-col n] [-lin n] [-min n]” in Arg.parse speclist (fun s -> ()) usagemsg; !cf

   3 OCaml Garbage Collection

   3.1 Representation of values

   • Pointers always end with 00 in binary (addresses are in number of bytes).
   • Integers are represented by shifting them 1 bit, setting the last bit to 1.
   • Constant constructors (i.e. variants without parameters) like None, [] and (), and other integer-like types (char, bool) are represented in the same way as integers.
   • Pointers are always to OCaml blocks. Variants with parameters, strings and OCaml arrays are stored as blocks.
   • A block starts with a header, followed by an array of values of size 1 word: either integer-like, or pointers.
   • The header stores the size of the block, the 2-bit color used for garbage collection, and 8-bit tag – which variant it is.
     • Therefore there can be at most about 240 variants with parameters in a variant type (some tag numbers are reserved).
     • Polymorphic variants are a different story.

   3.2 Generational Garbage Collection

   • OCaml has two heaps to store blocks: a small, continuous minor heap and a growing-as-necessary major heap.
   • Allocation simply moves the minor heap pointer (aka. the young pointer) and returns the pointed address.
     • Allocation of very large blocks uses the major heap instead.
   • When the minor heap runs out of space, it triggers the minor (garbage) collection, which uses the Stop & Copy algorithm.
   • Together with the minor collection, a slice of major (garbage) collection is performed to cleanup the major heap a bit.
     • The major heap is not cleaned all at once because it might stop the main program (i.e. our application) for too long.
     • Major collection uses the Mark & Sweep algorithm.
   • Great if most minor heap blocks are already not needed when collection starts – garbage does not slow down collection.

   3.3 Stop & Copy GC

   • Minor collection starts from a set of roots – young blocks that definitely are not garbage.
   • Besides the root set, OCaml also maintains the remembered set of minor heap blocks pointed at from the major heap.
     • Most mutations must check whether they assign a minor heap block to a major heap block field. This is called write barrier.
     • Immutable blocks cannot contain pointers from major to minor heap.
       • Unless they are lazy blocks.
   • Collection follows pointers in the root set and remembered set to find other used blocks.
   • Every found block is copied to the major heap.
   • At the end of collection, the young pointer is reset so that the minor heap is empty again.

   3.4 Mark & Sweep GC

   • Major collection starts from a separate root set – old blocks that definitely are not garbage.
   • Major garbage collection consists of a mark phase which colors blocks that are still in use and a sweep phase that searches for stretches of unused memory.
     • Slices of the mark phase are performed by-after each minor collection.
     • Unused memory is stored in a free list.
   • The “proper” major collection is started when a minor collection consumes the remaining free list. The mark phase is finished and sweep phase performed.
   • Colors:
     • gray: marked cells whose descendents are not yet marked;
     • black: marked cells whose descendents are also marked;
     • hatched: free list element;
     • white: elements previously being in use.
   • # let u = let l = ['c'; 'a'; 'm'] in List.tl l ;;``val u : char list = ['a'; 'm']``# let v = let r = ( ['z'] , u ) in match r with p -> (fst p) @ (snd p) ;;``val v : char list = ['z'; 'a'; 'm']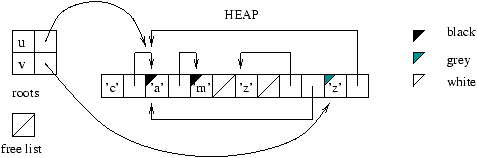
   • 
   • 

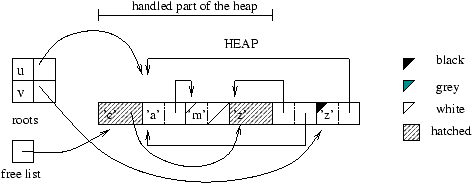
   4 Stack Frames and Closures

   • The nesting of procedure calls is reflected in the stack of procedure data.
   • The stretch of stack dedicated to a single function is stack frame aka. activation record.
   • Stack pointer is where we create new frames, stored in a special register.
   • Frame pointer allows to refer to function data by offset – data known early in compilation is close to the frame pointer.
   • Local variables are stored in the stack frame or in registers – some registers need to be saved prior to function call (caller-save) or at entry to a function (callee-save). OCaml avoids callee-save registers.
   • Up to 4-6 arguments can be passed in registers, remaining ones on stack.
     • Note that x86 architecture has a small number of registers.
   • Using registers, tail call optimization and function inlining can eliminate the use of stack entirely. OCaml compiler can also use stack more efficiently than by creating full stack frames as depicted below.
   • Static links point to stack frames of parent functions, so we can access stack-based data, e.g. arguments of a main function from inside aux.
   • A closure represents a function: it is a block that contains address of the function: either another closure or a machine-code pointer, and a way to access non-local variables of the function.
     • For partially applied functions, it contains the values of arguments and the address of the original function.
   • Escaping variables are the variables of a function f – arguments and local definitions – which are accessed from a nested function which is part of the returned value of f (or assigned to a mutable field).
     • Escaping variables must be either part of the closures representing the nested functions, or of a closure representing the function f – in the latter case, the nested functions must also be represented by closures that have a link to the closure of f.

   4.1 Tail Recursion

   • A function call f x within the body of another function g is in tail position if, roughly “calling f is the last thing that g will do before returning”.
   • Call inside try … with clause is not in tail position!
     • For efficient exceptions, OCaml stores traps for try-with on the stack with topmost trap in a register, after raise unwinding directly to the trap.
   • The steps for a tail call are:
     1. Move actual parameters into argument registers (if they aren’t already there).
     2. Restore callee-save registers (if needed).
     3. Pop the stack frame of the calling function (if it has one).
     4. Jump to the callee.
   • Bytecode always throws Stack_overflow exception on too deep recursion, native code will sometimes cause segmentation fault!
   • List.map from the standard distribution is not tail-recursive.

   4.2 Generated assembly

   • Let us look at examples from http://ocaml.org/tutorials/performance_and_profiling.html

   5 Profiling and Optimization

   • Steps of optimizing a program:
     1. Profile the program to find bottlenecks: where the time is spent.
     2. If possible, modify the algorithm used by the bottleneck to an algorithm with better asymptotic complexity.
     3. If possible, modify the bottleneck algorithm to access data less randomly, to increase cache locality.
        • Additionally, realtime systems may require avoiding use of huge arrays, traversed by the garbage collector in one go.
     4. Experiment with various implementations of data structures used (related to step 3).
     5. Avoid boxing and polymorphic functions. Especially for numerical processing. (OCaml specific.)
     6. Deforestation.
     7. Defunctorization.

   5.1 Profiling

   • We cover native code profiling because it is more useful.
     • It relies on the “Unix” profiling program gprof.
   • First we need to compile the sources in profiling mode: ocamlopt -p …

     • or using ocamlbuild when program source is in prog.ml:

       ocamlbuild prog.p.native --

   • The execution of program ./prog produces a file gmon.out
   • We call gprof prog > profile.txt

     • or when we used ocamlbuild as above:

       gprof prog.p.native > profile.txt

     • This redirects profiling analysis to profile.txt file.

   • The result profile.txt has three parts:
     1. List of functions in the program in descending order of the time which was spent within the body of the function, excluding time spent in the bodies of any other functions.
     2. A hierarchical representation of the time taken by each function, and the total time spent in it, including time spent in functions it called.
     3. A bibliography of function references.
   • It contains C/assembly function names like camlList__assoc_1169:
     • Prefix caml means function comes from OCaml source.
     • List__ means it belongs to a List module.
     • assoc is the name of the function in source.
     • Postfix _1169 is used to avoid name clashes, as in OCaml different functions often have the same names.
   • Example: computing words histogram for a large file, Optim0.ml.

   let readwords file =Imperative programming example. let input = openin file in let words = ref [] and more = ref true in tryLecture 6 read_lines function would stack-overflow while !more dobecause of the try-with clause. Scanf.fscanf input “%[a-zA-Z0-9’]%[a-zA-Z0-9’]” (fun b x -> words := x :: !words; more := x <> ““) done; List.rev (List.tl !words) with Endoffile -> List.rev !wordslet empty () = []let increment h w =Inefficient map update. try let c = List.assoc w h in (w, c+1) :: List.removeassoc w h with Notfound -> (w, 1)::hlet iterate f h =
   List.iter (fun (k,v)->f k v) hlet histogram words = List.foldleft increment (empty ()) wordslet = let words = readwords”./shakespeare.xml” in let words = List.revmap String.lowercase words in let h = histogram words in let output = openout “histogram.txt” in iterate (Printf.fprintf output “%s: %dn”) h; closeout output

   • Now we look at the profiling analysis, first part begins with:

     %   cumulative   self              self     total
    time   seconds   seconds    calls   s/call   s/call  name
    37.88      8.54     8.54 306656698    0.00     0.00  compare_val
    19.97     13.04     4.50   273169     0.00     0.00  camlList__assoc_1169
     9.17     15.10     2.07 633527269    0.00     0.00  caml_page_table_lookup
     8.72     17.07     1.97   260756    0.00  0.00 camlList__remove_assoc_1189
     7.10     18.67     1.60 612779467    0.00     0.00  caml_string_length
     4.97     19.79     1.12 306656692     0.00    0.00  caml_compare
     2.84     20.43     0.64                             caml_c_call
     1.53     20.77     0.35    14417     0.00     0.00  caml_page_table_modify
     1.07     21.01     0.24     1115     0.00     0.00  sweep_slice
     0.89     21.21     0.20      484     0.00     0.00  mark_slice

   • List.assoc and List.removeassoc high in the ranking suggests to us that increment could be the bottleneck.
     • They both use comparison which could explain why compare_val consumes the most of time.
   • Next we look at the interesting pieces of the second part: data about the increment function.
     • Each block, separated by —— lines, describes the function whose line starts with an index in brackets.
     • The functions that called it are above, the functions it calls below.

   index % time    self  children    called     name
   -----------------------------------------------
                   0.00    6.47  273169/273169  camlList__fold_left_1078 [7]
   [8]     28.7    0.00    6.47  273169         camlOptim0__increment_1038 [8]
                   4.50    0.00  273169/273169  camlList__assoc_1169 [9]
                  1.97    0.00  260756/260756  camlList__remove_assoc_1189 [11]

   • As expected, increment is only called by List.fold_left. But it seems to account for only 29% of time. It is because compare is not analysed correctly, thus not included in time for increment:

   -----------------------------------------------
                   1.12   12.13 306656692/306656692     caml_c_call [1]
   [2]     58.8    1.12   12.13 306656692         caml_compare [2]
                   8.54    3.60 306656692/306656698     compare_val [3]

   5.2 Algorithmic optimizations

   • (All times measured with profiling turned on.)

   • Optim0.ml asymptotic time complexity: \mathcal{O} (n^2), time: 22.53s.

     • Garbage collection takes 6% of time.
       • So little because data access wastes a lot of time.

   • Optimize the data structure, keep the algorithm.

     let empty () = Hashtbl.create 511let increment h w = try let c = Hashtbl.find h w in Hashtbl.replace h w (c+1); h with Notfound -> Hashtbl.add h w 1; hlet iterate f h = Hashtbl.iter f h

     Optim1.ml asymptotic time complexity: \mathcal{O} (n), time: 0.63s.

     • Garbage collection takes 17% of time.

   • Optimize the algorithm, keep the data structure.

     let histogram words = let words = List.sort String.compare words in let k,c,h = List.foldleft (fun (k,c,h) w -> if k = w then k, c+1, h else w, 1, ((k,c)::h)) (““, 0, []) words in (k,c)::h

     Optim2.ml asymptotic time complexity: \mathcal{O} (n \log n), time: 1s.

     • Garbage collection takes 40% of time.

   • Optimizing for cache efficiency is more advanced, we will not attempt it.

   • With algorithmic optimizations we should be concerned with asymptotic complexity in terms of the \mathcal{O} (\cdot) notation, but we will not pursue complexity analysis in the remainder of the lecture.

   5.3 Low-level optimizations

   • Optimizations below have been made for educational purposes only.

   • Avoid polymorphism in generic comparison function (=).

     let rec assoc x = function [] -> raise Notfound | (a,b)::l -> if String.compare a x = 0 then b else assoc x llet rec removeassoc x = function | [] -> [] | (a, b as pair) :: l -> if String.compare a x = 0 then l else pair :: removeassoc x l

     Optim3.ml (based on Optim0.ml) time: 19s.

     • Despite implementation-wise the code is the same, as String.compare = Pervasives.compare inside module String, and List.assoc is like above but uses Pervasives.compare!
     • We removed polymorphism, no longer caml_compare_val function.
     • Usually, adding type annotations would be enough. (Useful especially for numeric types int, float.)

   • Deforestation means removing intermediate data structures.

     let readtohistogram file = let input = openin file in let h = empty () and more = ref true in try while !more do Scanf.fscanf input “%[a-zA-Z0-9’]%[a-zA-Z0-9’]” (fun b w -> let w = String.lowercase w in increment h w; more := w <> ““)
     done; h with Endoffile -> h

     Optim4.ml (based on Optim1.ml) time: 0.51s.

     • Garbage collection takes 8% of time.
       • So little because we have eliminated garbage.

   • Defunctorization means computing functor applications by hand.

     • There was a tool ocamldefun but it is out of date.
     • The slight speedup comes from the fact that functor arguments are implemented as records of functions.

   5.4 Comparison of data structure implementations

   • We perform a rough comparison of association lists, tree-based maps and hashtables. Sets would give the same results.
   • We always create hashtables with initial size 511.
   • 10^7 operations of: adding an association (creation), finding a key that is in the map, finding a key out of a small number of keys not in the map.
   • First row gives sizes of maps. Time in seconds, to two significant digits.

   create:
   assoc list	0.25	0.25	0.18	0.19	0.17	0.22	0.19	0.19	0.19
   tree map	0.48	0.81	0.82	1.2	1.6	2.3	2.7	3.6	4.1	5.1
   hashtable	27	9.1	5.5	4	2.9	2.4	2.1	1.9	1.8	3.7

   create:
   tree map	6.5	8	9.8	15	19	26	34	41	51	67	80	130
   hashtable	4.8	5.6	6.4	8.4	12	15	19	20	22	24	23	33

   found:
   assoc list	1.1	1.5	2.5	4.2	8.1	17	30	60	120
   tree map	1	1.1	1.3	1.5	1.9	2.1	2.5	2.8	3.1	3.6
   hashtable	1.4	1.5	1.4	1.4	1.5	1.5	1.6	1.6	1.8	1.8

   found:
   tree map	4.3	5.2	6	7.6	9.4	12	15	17	19	24	28	32
   hashtable	1.8	2	2.5	3.1	4	5.1	5.9	6.4	6.8	7.6	6.7	7.5

   not found:
   assoc list	1.8	2.6	4.6	8	16	32	60	120	240
   tree map	1.5	1.5	1.8	2.1	2.4	2.7	3	3.2	3.5	3.8
   hashtable	1.4	1.4	1.5	1.5	1.6	1.5	1.7	1.9	2	2.1

   not found:
   tree map	4.2	4.3	4.7	4.9	5.3	5.5	6.1	6.3	6.6	7.2	7.5	7.3
   hashtable	1.8	1.9	2	1.9	1.9	1.9	2	2	2.2	2	2	1.9

   • Using lists makes sense for up to about 15 elements.
   • Unfortunately OCaml and Haskell do not encourage the use of efficient maps, the way Scala and Python have built-in syntax for them.

   6 Parsing: ocamllex and Menhir

   • Parsing means transforming text, i.e. a string of characters, into a data structure that is well fitted for a given task, or generally makes information in the text more explicit.
   • Parsing is usually done in stages:
     1. Lexing or tokenizing, dividing the text into smallest meaningful pieces called lexemes or tokens,
     2. composing bigger structures out of lexemes/tokens (and smaller structures) according to a grammar.
        • Alternatively to building such hierarchical structure, sometimes we build relational structure over the tokens, e.g. dependency grammars.
   • We will use ocamllex for lexing, whose rules are like pattern matching functions, but with patterns being regular expressions.
   • We will either consume the results from lexer directly, or use Menhir for parsing, a successor of ocamlyacc, belonging to the yacc/bison family of parsers.

   6.1 Lexing with ocamllex

   • The format of lexer definitions is as follows: file with extension .mll

     { header }let ident1 = regexp …rule entrypoint1 [arg1… argN] = parse regexp { action1 }| …| regexp { actionN }and entrypointN [arg1? argN] = parse …and …{ trailer }

     • Comments are delimited by (* and *), as in OCaml.
     • The parse keyword can be replaced by the shortest keyword.
     • ”Header”, “trailer”, “action1”, … “actionN” are arbitrary OCaml code.
     • There can be multiple let-clauses and rule-clauses.

   • Let-clauses are shorthands for regular expressions.

   • Each rule-clause entrypoint defines function(s) that as the last argument (after arg1… argN if N>0) takes argument lexbuf of type Lexing.lexbuf.

     • lexbuf is also visible in actions, just as a regular argument.
     • entrypoint1… entrypointN can be mutually recursive if we need to read more before we can return output.
     • It seems rule keyword can be used only once.

   • We can use lexbuf in actions:

     • Lexing.lexeme lexbuf – Return the matched string.
     • Lexing.lexemechar lexbuf n – Return the nth character in the matched string. The first character corresponds to n = 0.
     • Lexing.lexemestart/lexemeend lexbuf – Return the absolute position in the input text of the beginning/end of the matched string (i.e. the offset of the first character of the matched string). The first character read from the input text has offset 0.

   • The parser will call an entrypoint when it needs another lexeme/token.

   • The syntax of regular expressions

     • ‘c’ – match the character ‘c’
     • _ – match a single character
     • eof – match end of lexer input
     • “string” – match the corresponding sequence of characters
     • [character set] – match the character set, characters ‘c’ and ranges of characters ‘c’-‘d’ separated by space
     • [^character set] – match characters outside the character set
     • [character set 1] # [character set 2] – match the difference, i.e. only characters in set 1 that are not in set 2
     • regexp* – (repetition) match the concatenation of zero or more strings that match regexp
     • regexp+ – (strict repetition) match the concatenation of one or more strings that match regexp
     • regexp? – (option) match the empty string, or a string matching regexp.
     • regexp1 | regexp2 – (alternative) match any string that matches regexp1 or regexp2
     • regexp1 regexp2 – (concatenation) match the concatenation of two strings, the first matching regexp1, the second matching regexp2.
     • ( regexp ) – match the same strings as regexp
     • ident – reference the regular expression bound to ident by an earlier let ident = regexp definition
     • regexp as ident – bind the substring matched by regexp to identifier ident.

     The precedences are: # highest, followed by *, +, ?, concatenation, |, as.

   • The type of as ident variables can be string, char, string option or char option

     • char means obviously a single character pattern
     • option means situations like (regexp as ident)? or regexp1|(regexp2 as ident)
     • The variables can repeat in the pattern (unlike in normal paterns) – meaning both regexpes match the same substrings.

   • ocamllex Lexer.mll produces the lexer code in Lexer.ml

     • ocamlbuild will call ocamllex and ocamlyacc/menhir if needed

   • Unfortunately if the lexer patterns are big we get an error:

     transition table overflow, automaton is too big

   6.1.1 Example: Finding email addresses

   • We mine a text file for email addresses, that could have been obfuscated to hinder our job…

   • To compile and run Emails.mll, processing a file email_corpus.xml:

     ocamlbuild Emails.native -- email_corpus.xml

   {The header with OCaml code. open LexingMake accessing Lexing easier. let nextline lexbuf =Typical lexer function: move position to next line. let pos = lexbuf.lexcurrp in lexbuf.lexcurrp <- { pos with poslnum = pos.poslnum + 1; posbol = pos.poscnum; } type state =Which step of searching for address we’re at: | SeekSeek: still seeking, Addr (true…): possibly finished, | Addr of bool * string * string listAddr (false…): no domain.

   let report state lexbuf =Report the found address, if any. match state with | Seek -> () | Addr (false, , ) -> () | Addr (true, name, addr) ->With line at which it is found. Printf.printf “%d: %s@%sn” lexbuf.lexcurrp.poslnum name (String.concat “.” (List.rev addr))}let newline = (‘’ | “”)Regexp for end of line.let addrchar = [‘a’-‘z’‘A’-‘Z’‘0’-‘9’‘-’’’]let atwsymb = “where” | “WHERE” | “at” | “At” | “AT”let atnwsymb = ‘@’ | “@” | “@”let opensymb = ’ ‘*’(’ ’ ‘* |’ ‘+Demarcate a possible @let closesymb =’ ‘*’)’’ ‘* |’ ’+or . symbol.let atsepsymb = opensymb? atnwsymb closesymb? | opensymb atwsymb closesymb

   let dotwsymb = “dot” | “DOT” | “dt” | “DT”let domwsymb = dotwsymb | “dom” | “DOM”Obfuscation for last dot.let dotsepsymb = opensymb dotwsymb closesymb |
   opensymb? ‘.’ closesymb?let domsepsymb = opensymb domwsymb closesymb |
   opensymb? ‘.’ closesymb?let addrdom = addrchar addrcharRestricted form of last part| “edu” | “EDU” | “org” | “ORG” | “com” | “COM”of address.rule email state = parse| newlineCheck state before moving on.{ report state lexbuf; nextline lexbuf; email Seek lexbuf }\swarrowDetected possible start of address.| (addrchar+ as name) atsepsymb (addrchar+ as addr) { email (Addr (false, name, [addr])) lexbuf }

   domsepsymb (addrdom as dom)Detected possible finish of address. { let

   state = match state with | Seek -> SeekWe weren’t looking at an address. | Addr (, name, addrs) ->Bingo. Addr (true, name, dom::addrs) in email state lexbuf }| dotsepsymb (addrchar+ as addr)Next part of address – { let state =must be continued. match state with | Seek -> Seek | Addr (, name, addrs) ->
   Addr (false, name, addr::addrs) in email state lexbuf }| eofEnd of file – end loop.{ report state lexbuf }|Some boring character – not looking at an address yet.{ report state lexbuf; email Seek lexbuf }{The trailer with OCaml code. let =Open a file and start mining for email addresses. let ch = openin Sys.argv.(1) in email Seek (Lexing.fromchannel ch); closein chClose the file at the end.}

   6.2 Parsing with Menhir

   • The format of parser definitions is as follows: file with extension .mly

     %{ header %}OCaml code put in front.%parameter < M : signature >Parameters make a functor.%token < type1 > Token1 Token2Terminal productions, variants%token < type3 > Token3returned from lexer.%token NoArgTokenWithout an argument, e.g. keywords or symbols.%nonassoc Token1This token cannot be stacked without parentheses.%left Token3Associates to left,%right Token2to right.%type < type4 > rule1Type of the action of the rule.%start < type5 > rule2The entry point of the grammar.%%Separate out the rules part.%inline rule1 (id1, …, inN) :Inlined rules can propagate priorities.|production1 { action1 }If production matches, perform action.|production2 |production3Several productions{ action2 }with the same action.

     %public rule2 :Visible in other files of the grammar. | production4 { action4 }%public rule3 :Override precedence of production5 to that of productions | production5 { action5 } %prec Token1ending with Token1%%The separations are needed even if the sections are empty.trailerOCaml code put at the end of generated source.

   • Header, actions and trailer are OCaml code.

   • Comments are (* … ) in OCaml code, / … */ or // … outisde

   • Rules can optionally be separated by ;

   • %parameter turns the whole resulting grammar into a functor, multiple parameters are allowed. The parameters are visible in %{…%}.

   • Terminal symbols Token1 and Token2 are both variants with argument of type type1, called their semantic value.

   • rule1… ruleN must be lower-case identifiers.

   • Parameters id1… idN can be lower- or upper-case.

   • Priorities, i.e. precedence, are declared implicitly: %nonassoc, %left, %right list tokens in increasing priority (Token2 has highest precedence).

     • Higher precedence = a rule is applied even when tokens so far could be part of the other rule.
     • Precedence of a production comes from its rightmost terminal.
     • %left/%right means left/right associativity: the rule will/won’t be applied if the “other” rule is the same production.

   • %start symbols become names of functions exported in the .mli file to invoke the parser. They are automatically %public.

   • %public rules can even be defined over multiple files, with productions joined by |.

   • The syntax of productions, i.e. patterns, each line shows one aspect, they can be combined:

     rule2 Token1 rule3Match tokens in sequence with Token1 in the middle.a=rule2 t=Token3Name semantic values produced by rules/tokens.rule2; Token3Parts of pattern can be separated by semicolon.rule1(arg1,…,argN)Use a rule that takes arguments.rule2?Shorthand for option(rule2)rule2+Shorthand for nonemptylist(rule2)rule2*Shorthand for list(rule2)

   • Always-visible “standard library” – most of rules copied below:

     %public option(X): /* nothing */ { None }| x = X { Some x }%public %inline pair(X, Y): x = X; y = Y { (x, y) }

     %public %inline separatedpair(X, sep, Y): x = X; sep; y = Y { (x, y) }%public %inline delimited(opening, X, closing): opening; x = X; closing
     { x }%public list(X): /* nothing */ { [] }| x = X; xs = list(X) { x :: xs }%public nonemptylist(X): x = X { [ x ] }| x = X; xs = nonemptylist(X) { x :: xs }%public %inline separatedlist(separator, X):
     xs = loption(separatednonemptylist(separator, X)) { xs }

     %public separatednonemptylist(separator, X): x = X { [ x ] }| x = X; separator; xs = separatednonemptylist(separator, X) { x :: xs }

   • Only left-recursive rules are truly tail-recursive, as in:

     declarations:| { [] }| ds = declarations; option(COMMA); d = declaration { d :: ds }

     • This is opposite to code expressions (or recursive descent parsers), i.e. if both OK, first rather than last invocation should be recursive.

   • Invocations can be nested in arguments, e.g.:

     plist(X):| xs = loption(Like option, but returns a list.
     delimited(LPAREN, separatednonemptylist(COMMA, X),
     RPAREN)) { xs }

   • Higher-order parameters are allowed.

     procedure(list):| PROCEDURE ID list(formal) SEMICOLON block SEMICOLON {…}

   • Example where inlining is required (besides being an optimization)

     %token < int > INT%token PLUS TIMES%left PLUS%left TIMESMultiplication has higher priority.%%expression:| i = INT { i }\swarrow Without inlining, would not distinguish priorities.| e = expression; o = op; f = expression { o e f }%inline op:Inline operator – generate corresponding rules.| PLUS { ( + ) }| TIMES { ( * ) }

   • Menhir is an \operatorname{LR} (1) parser generator, i.e. it fails for grammars where looking one token ahead, together with precedences, is insufficient to determine whether a rule applies.

     • In particular, only unambiguous grammars.

   • Although \operatorname{LR} (1) grammars are a small subset of context free grammars, the semantic actions can depend on context: actions can be functions that take some form of context as input.

   • Positions are available in actions via keywords $startpos(x) and $endpos(x) where x is name given to part of pattern.

     • Do not use the Parsing module from OCaml standard library.

   6.2.1 Example: parsing arithmetic expressions

   • Example based on a Menhir demo. Due to difficulties with ocamlbuild, we use option --external-tokens to provide type token directly rather than having it generated.

   • File lexer.mll:

     { type token = | TIMES | RPAREN | PLUS | MINUS | LPAREN
     | INT of (int) | EOL | DIV exception Error of string}

     rule line = parse| ([‘n’]* ‘n’) as line { line }| eof { exit 0 }and token = parse| [’ ’ ‘t’] { token lexbuf }| ‘n’ { EOL }| [‘0’-‘9’]+ as i { INT (intofstring i) }| ‘+’ { PLUS }| ‘-’ { MINUS }| ’*’ { TIMES }| ‘/’ { DIV }| ‘(’ { LPAREN }| ‘)’ { RPAREN }| eof { exit 0 }| { raise (Error (Printf.sprintf “At offset %d: unexpected character.n” (Lexing.lexemestart lexbuf))) }

   • File parser.mly:

     %token INTWe still need to define tokens,%token PLUS MINUS TIMES DIVMenhir does its own checks.%token LPAREN RPAREN%token EOL%left PLUS MINUS /* lowest precedence /%left TIMES DIV / medium precedence /%nonassoc UMINUS / highest precedence /%parameter<Semantics : sig type number val inject: int -> number val ( + ): number -> number -> number val ( - ): number -> number -> number val ( ): number -> number -> number val ( / ): number -> number -> number val ( \sim-): number -> numberend>%start <Semantics.number> main%{ open Semantics %}

     %%main:| e = expr EOL { e }expr:| i = INT { inject i }| LPAREN e = expr RPAREN { e }| e1 = expr PLUS e2 = expr { e1 + e2 }| e1 = expr MINUS e2 = expr { e1 - e2 }| e1 = expr TIMES e2 = expr { e1 * e2 }| e1 = expr DIV e2 = expr { e1 / e2 }| MINUS e = expr %prec UMINUS { - e }

   • File calc.ml:

     module FloatSemantics = struct type number = float let inject = floatofint let ( + ) = ( +. ) let ( - ) = ( -. ) let ( * ) = ( *. ) let ( / ) = ( /. ) let (\sim- ) = (\sim-. )endmodule FloatParser = Parser.Make(FloatSemantics)

     let () = let stdinbuf = Lexing.fromchannel stdin in while true do let linebuf = Lexing.fromstring (Lexer.line stdinbuf) in try
     Printf.printf “%.1fn%!” (FloatParser.main Lexer.token linebuf)
     with | Lexer.Error msg -> Printf.fprintf stderr “%s%!” msg | FloatParser.Error -> Printf.fprintf stderr “At offset %d: syntax error.n%!” (Lexing.lexemestart linebuf) done

   • Build and run command:

     ocamlbuild calc.native -use-menhir -menhir "menhir parser.mly --base parser --external-tokens Lexer" --

     • Other grammar files can be provided besides parser.mly
     • --base gives the file (without extension) which will become the module accessed from OCaml
     • --external-tokens provides the OCaml module which defines the token type

   6.2.2 Example: a toy sentence grammar

   • Our lexer is a simple limited part-of-speech tagger. Not re-entrant.
   • For debugging, we log execution in file log.txt.
   • File EngLexer.mll:

   { type sentence = {Could be in any module visible to EngParser. subject : string;The actor/actors, i.e. subject noun. action : string;The action, i.e.  verb. plural : bool;Whether one or multiple actors. adjs : string list;Characteristics of actor. advs : string listCharacteristics of action. }

   type token = | VERB of string | NOUN of string | ADJ of string | ADV of string | PLURAL | SINGULAR | ADET | THEDET | SOMEDET | THISDET | THATDET | THESEDET | THOSEDET | COMMACNJ | ANDCNJ | DOTPUNCT let tokstr = function …Print the token. let adjectives =Recognized adjectives. [“smart”; “extreme”; “green”; “slow”; “old”; “incredible”; “quiet”; “diligent”; “mellow”; “new”] let logfile = openout “log.txt”File with debugging information.let log s = Printf.fprintf logfile “%sn%!” s let lasttok = ref DOTPUNCTState for better tagging.

   let tokbuf = Queue.create ()Token buffer, since single word let push w =is sometimes two tokens. log (“lex:”tokstr w);Log lexed token. lasttok := w; Queue.push w tokbuf exception LexError of string}let alphanum = [‘0’-‘9’ ‘a’-‘z’ ‘A’-‘Z’ ’’’ ‘-’]rule line = parseFor line-based interface.| ([‘’]* ‘’) as l { l }| eof { exit 0 }and lexword = parse| [’ ’ ’]Skip whitespace. { lexword lexbuf }| ‘.’ { push DOTPUNCT }End of sentence.| “a” { push ADET } | “the” { push THEDET }‘‘Keywords’‘.| “some” { push SOMEDET }| “this” { push THISDET } | “that” { push THATDET }| “these” { push THESEDET } | “those” { push THOSEDET }| “A” { push ADET } | “The” { push THEDET }| “Some” { push SOMEDET }| “This” { push THISDET } | “That” { push THATDET }| “These” { push THESEDET } | “Those” { push THOSEDET }| “and” { push ANDCNJ }|’,’ { push COMMACNJ }| (alphanum+ as w) “ly”Adverb is adjective that ends in ‘‘ly’’.{
   if List.mem w adjectives then push (ADV w) else if List.mem (w”le”) adjectives then push (ADV (w”le”)) else (push (NOUN w); push SINGULAR) }

   (alphanum+ as w) “s”Plural noun or singular verb.{ if List.mem w

   adjectives then push (ADJ w) else match !lasttok with | THEDET | SOMEDET | THESEDET | THOSEDET | DOTPUNCT | ADJ -> push (NOUN w); push PLURAL | -> push (VERB w); push SINGULAR }| alphanum+ as wNoun contexts vs. verb contexts.{ if List.mem w adjectives then push (ADJ w) else match !lasttok with | ADET | THEDET | SOMEDET | THISDET | THATDET | DOTPUNCT | ADJ -> push (NOUN w); push SINGULAR
   | -> push (VERB w); push PLURAL }

    as w { raise (LexError (“Unrecognized character”

   Char.escaped w)) }{ let lexeme lexbuf =The proper interface reads from the token buffer. if Queue.isempty tokbuf then lexword lexbuf; Queue.pop tokbuf}

   • File EngParser.mly:

   %{ open EngLexerSource of the token type and sentence type.%}%token VERB NOUN ADJ ADVOpen word classes.%token PLURAL SINGULARNumber marker.%token ADET THEDET SOMEDET THISDET THATDET‘‘Keywords’’.%token THESEDET THOSEDET%token COMMACNJ ANDCNJ DOTPUNCT%start <EngLexer.sentence> sentenceGrammar entry.%%

   %public %inline sep2list(sep1, sep2, X):General purpose.| xs = separatednonemptylist(sep1, X) sep2 x=X { xs @ [x] }We use it for ‘‘comma-and’’ lists:| x=option(X)smart, quiet and diligent. { match x with None->[] | Some x->[x] }singonlydet:How determiners relate to number.| ADET | THISDET | THATDET { log “prs: singonlydet” }pluonlydet:| THESEDET | THOSEDET { log “prs: pluonlydet” }otherdet:| THEDET | SOMEDET { log “prs: otherdet” }np(det):| det adjs=list(ADJ) subject=NOUN { log “prs: np”; adjs, subject }vp(NUM):| advs=separatedlist(ANDCNJ,ADV) action=VERB NUM| action=VERB NUM advs=sep2list(COMMACNJ,ANDCNJ,ADV) { log “prs: vp”; action, advs }

   sent(det,NUM):Sentence parameterized by number.| adjsub=np(det) NUM vbadv=vp(NUM) { log “prs: sent”; {subject=snd adjsub; action=fst vbadv; plural=false; adjs=fst adjsub; advs=snd vbadv} }vbsent(NUM):Unfortunately, it doesn’t always work…| NUM vbadv=vp(NUM)
   { log “prs: vbsent”; vbadv }sentence:Sentence, either singular or plural number.| s=sent(singonlydet,SINGULAR) DOTPUNCT { log “prs: sentence1”;
   {s with plural = false} }| s=sent(pluonlydet,PLURAL) DOTPUNCT { log “prs: sentence2”; {s with plural = true} }

   adjsub=np(otherdet) vbadv=vbsent(SINGULAR) DOTPUNCT { log “prs:

   sentence3”;Because parser allows only one token look-ahead {subject=snd adjsub; action=fst vbadv; plural=false; adjs=fst adjsub; advs=snd vbadv} }| adjsub=np(otherdet) vbadv=vbsent(PLURAL) DOTPUNCT { log “prs: sentence4”;we need to factor-out the ‘‘common subset’’. {subject=snd adjsub; action=fst vbadv; plural=true; adjs=fst adjsub; advs=snd vbadv} }

   • File Eng.ml is the same as calc.ml from previous example:

   open EngLexerlet () = let stdinbuf = Lexing.fromchannel stdin in while true do (* Read line by line. *) let linebuf = Lexing.fromstring (line stdinbuf) in

   try      (* Run the parser on a single line of input. *)      let s = 

   EngParser.sentence lexeme linebuf in Printf.printf
   “subject=%s=%b=%s=%snadvs=%s%!” s.subject s.plural (String.concat “,” s.adjs) s.action (String.concat “,” s.advs) with | LexError msg -> Printf.fprintf stderr “%sn%!” msg | EngParser.Error -> Printf.fprintf stderr “At offset %d: syntax error.n%!” (Lexing.lexemestart linebuf) done

   • Build & run command:

     ocamlbuild Eng.native -use-menhir -menhir "menhir EngParser.mly --base EngParser --external-tokens EngLexer" --

   7 Example: Phrase search

   • In lecture 6 we performed keyword search, now we turn to phrase search i.e. require that given words be consecutive in the document.

   • We start with some English-specific transformations used in lexer:

     let whorpronoun w = w = “where” || w = “what” || w = “who” || w = “he” || w = “she” || w = “it” || w = “I” || w = “you” || w = “we” || w = “they”let abridged w1 w2 =Remove shortened forms like I’ll or press’d. if w2 = “ll” then [w1; “will”] else if w2 = “s” then if whorpronoun w1 then [w1; “is”] else [“of”; w1] else if w2 = “d” then [w1”ed”] else if w1 = “o” || w1 = “O” then if w2.[0] = ‘e’ && w2.[1] = ‘r’ then [w1”v”w2] else [“of”; w2] else if w2 = “t” then [w1; “it”] else [w1”’“w2]

   • For now we normalize words just by lowercasing, but see exercise 8.

   • In lexer we tokenize text: separate words and normalize them.

     • We also handle simple aspects of XML syntax.

   • We store the number of each word occurrence, excluding XML tags.

   { open IndexParser let word = ref 0 let linebreaks = ref [] let commentstart = ref Lexing.dummypos let resetasfile lexbuf s =General purpose lexer function: let pos = lexbuf.Lexing.lexcurrp instart lexing from a file. lexbuf.Lexing.lexcurrp <- { pos with Lexing.poslnum = 1;
   posfname = s; posbol = pos.Lexing.poscnum; }; linebreaks := []; word := 0 let nextline lexbuf =Old friend. …Besides changing position, remember a line break. linebreaks := !word :: !linebreaks

   let parseerrormsg startpos endpos report =General purpose lexer function:
   let clbeg =report a syntax error. startpos.Lexing.poscnum - startpos.Lexing.posbol in ignore (Format.flushstrformatter ());
   Printf.sprintf “File”%s”, lines %d-%d, characters %d-%d: %sn”
   startpos.Lexing.posfname startpos.Lexing.poslnum endpos.Lexing.poslnum clbeg (clbeg+(endpos.Lexing.poscnum - startpos.Lexing.poscnum))
   report}let alphanum = [‘0’-‘9’ ‘a’-‘z’ ‘A’-‘Z’]let newline = (‘n’ | “rn”)let xmlstart = (“” | “?>”)rule token = parse | [’ ’ ‘t’] { token lexbuf } | newline { nextline lexbuf; token lexbuf }

   | ‘<’ alphanum+ ‘>’ as wDedicated token variants for XML tags.{ OPEN w } | “</” alphanum+ ‘>’ as w { CLOSE w } | “’tis” { word := !word+2; WORDS [“it”, !word-1; “is”, !word] } | “‘Tis” { word := !word+2; WORDS [“It”, !word-1; “is”, !word] } | “o’clock” { incr word; WORDS [“o’clock”, !word] } | “O’clock” { incr word; WORDS [“O’clock”, !word] } | (alphanum+ as w1)’’’ (alphanum+ as w2) { let words = EngMorph.abridged w1 w2 in let words = List.map (fun w -> incr word; w, !word) words in WORDS words } | alphanum+ as w { incr word; WORDS [w, !word] } |”&” { incr word; WORDS [“&”, !word] }

   | [‘.’ ‘!’ ‘?’] as pDedicated tokens for punctuation { SENTENCE (Char.escaped p) }so that it doesn’t break phrases. | “–” { PUNCT “–” } | [‘,’ ‘:’ ’’’ ‘-’ ‘;’] as p { PUNCT (Char.escaped p) } | eof { EOF } | xmlstart { commentstart := lexbuf.Lexing.lexcurrp; let s = comment [] lexbuf in COMMENT s } | { let pos = lexbuf.Lexing.lexcurrp in let pos’ = {pos with Lexing.poscnum = pos.Lexing.poscnum + 1} in Printf.printf “%s%!”
   (parseerrormsg pos pos’ “lexer error”); failwith “LEXER ERROR” }

   and comment strings = parse | xmlend { String.concat “” (List.rev strings) } | eof { let pos = !commentstart in let pos’ = lexbuf.Lexing.lexcurrp in Printf.printf “%sn%!” (parseerrormsg pos pos’ “lexer error: unclosed comment”); failwith “LEXER ERROR” } | newline { nextline lexbuf; comment (Lexing.lexeme lexbuf :: strings) lexbuf } | { comment (Lexing.lexeme lexbuf :: strings) lexbuf }

   • Parsing: the inverted index and the query.

   type token =| WORDS of (string * int) list| OPEN of string | CLOSE of string | COMMENT of string| SENTENCE of string | PUNCT of string| EOF

   let invindex update ii lexer lexbuf = let rec aux ii = match lexer lexbuf with | WORDS ws -> let ws = List.map (fun (w,p)->EngMorph.normalize w, p) ws in aux (List.foldleft update ii ws) | OPEN | CLOSE | SENTENCE | PUNCT | COMMENT -> aux ii
   | EOF -> ii in aux ii

   let phrase lexer lexbuf = let rec aux words = match lexer lexbuf with | WORDS ws -> let ws = List.map (fun (w,p)->EngMorph.normalize w) ws in aux (List.revappend ws words) | OPEN | CLOSE | SENTENCE | PUNCT | COMMENT -> aux words | EOF -> List.rev words in aux []

   1 Naive implementation of phrase search

   • We need postings lists with positions of words rather than just the document or line of document they belong to.
   • First approach: association lists and merge postings lists word-by-word.

   let update ii (w, p) = try let ps = List.assoc w ii inAdd position to the postings list of w. (w, p::ps) :: List.removeassoc w ii with Notfound -> (w, [p])::iilet empty = []let find w ii = List.assoc w iilet mapv f ii = List.map (fun (k,v)->k, f v) iilet index file = let ch = openin file in let lexbuf = Lexing.fromchannel ch in EngLexer.resetasfile lexbuf file; let ii = IndexParser.invindex update empty EngLexer.token lexbuf in closein ch;Keep postings lists in increasing order. mapv List.rev ii, List.rev !EngLexer.linebreakslet findline linebreaks p =Recover the line in document of a position. let rec aux line = function | [] -> line
   | bp:: when p < bp -> line | ::breaks -> aux (line+1) breaks in aux 1 linebreakslet search (ii, linebreaks) phrase = let lexbuf = Lexing.fromstring phrase in EngLexer.resetasfile lexbuf (“search phrase:”phrase); let phrase = IndexParser.phrase EngLexer.token lexbuf in let rec aux wpos = functionMerge postings lists for words in query: | [] -> wposno more words in query;| w::ws ->for positions of w, keep those that are next to let nwpos = find w ii infiltered positions of previous word. aux (List.filter (fun p->List.mem (p-1) wpos) nwpos) ws in let wpos = match phrase with | [] -> []No results for an empty query.
   | w::ws -> aux (find w ii) ws in List.map (findline linebreaks) wposAnswer in terms of document lines.

   let shakespeare = index “./shakespeare.xml”let query q = let lines = search shakespeare q in Printf.printf “%s: lines %sn%!” q (String.concat “,” (List.map stringofint lines))

   • Test: 200 searches of the queries:

     [“first witch”; “wherefore art thou”; “captain’s captain”; “flatter’d”; “of Fulvia”; “that which we call a rose”; “the undiscovered country”]

   • Invocation: ocamlbuild InvIndex.native -libs unix --

   • Time: 7.3s

   2 Replace association list with hash table

   • I recommend using either OCaml Batteries or OCaml Core – replacement for the standard library. Batteries has efficient Hashtbl.map (our mapv).
   • Invocation: ocamlbuild InvIndex1.native -libs unix --
   • Time: 6.3s

   3 Replace naive merging with ordered merging

   • Postings lists are already ordered.
   • Invocation: ocamlbuild InvIndex2.native -libs unix --
   • Time: 2.5s

   4 Bruteforce optimization: biword indexes

   • Pairs of words are much less frequent than single words so storing them means less work for postings lists merging.

   • Can result in much bigger index size: \min (W^2, N) where W is the number of distinct words and N the total number of words in documents.

   • Invocation that gives us stack backtraces:

     ocamlbuild InvIndex3.native -cflag -g -libs unix; export OCAMLRUNPARAM="b"; ./InvIndex3.native

   • Time: 2.4s – disappointing.

   7.1 Smart way: Information Retrieval G.V. Cormack et al.

   • You should classify your problem and search literature for state-of-the-art algorithm to solve it.
   • The algorithm needs a data structure for inverted index that supports:
     • first(w) – first position in documents at which w appears
     • last(w) – last position of w
     • next(w,cp) – first position of w after position cp
     • prev(w,cp) – last position of w before position cp
   • We develop next and prev operations in stages:
     • First, a naive (but FP) approach using the Set module of OCaml.
       • We could use our balanced binary search tree implementation to avoid the overhead due to limitations of Set API.
     • Then, binary search based on arrays.
     • Imperative linear search.
     • Imperative galloping search optimization of binary search.

   7.1.1 The phrase search algorithm

   • During search we maintain current position cp of last found word or phrase.
   • Algorithm is almost purely functional, we use Not_found exception instead of option type for convenience.

   let rec nextphrase ii phrase cp =Return the beginning and end position let rec aux cp = functionof occurrence of phrase after position cp. | [] -> raise NotfoundEmpty phrase counts as not occurring. | [w] ->Single or last word of phrase has the same let np = next ii w cp in np, npbeg. and end position.| w::ws ->After locating the endp. move back. let np, fp = aux (next ii w cp) ws in prev ii w np, fp inIf distance is this small, let np, fp = aux cp phrase inwords are consecutive. if fp - np = List.length phrase - 1 then np, fp else nextphrase ii phrase fp

   let search (ii, linebreaks) phrase = let lexbuf = Lexing.fromstring phrase in EngLexer.resetasfile lexbuf (“search phrase:”phrase); let phrase = IndexParser.phrase EngLexer.token lexbuf in let rec aux cp = tryFind all occurrences of the phrase. let np, fp = nextphrase ii phrase cp in
   np :: aux fp with Notfound -> [] inMoved past last occurrence.
   List.map (findline linebreaks) (aux (-1))

   7.1.2 Naive but purely functional inverted index

   module S = Set.Make(struct type t=int let compare i j = i-j end)let update ii (w, p) = (try let ps = Hashtbl.find ii w in Hashtbl.replace ii w (S.add p ps) with Notfound -> Hashtbl.add ii w (S.singleton p)); iilet first ii w = S.minelt (find w ii)The functions raise Not_foundlet last ii w = S.maxelt (find w ii)whenever such position would not exist.let prev ii w cp = let ps = find w ii inSplit the set into elements let smaller, , = S.split cp ps insmaller and bigger than cp. S.maxelt smallerlet next ii w cp = let ps = find w ii in let , , bigger = S.split cp ps in S.minelt bigger

   • Invocation: ocamlbuild InvIndex4.native -libs unix --
   • Time: 3.3s – would be better without the overhead of S.split.

   7.1.3 Binary search based inverted index

   let prev ii w cp = let ps = find w ii in let rec aux b e =We implement binary search separately for prev if e-b <= 1 then ps.(b)to make sure here we return less than cp else let m = (b+e)/2 in if ps.(m) < cp then aux m eelse aux b m in let l = Array.length ps in if l = 0 || ps.(0) >= cp then raise Notfound else aux 0 (l-1)let next ii w cp = let ps = find w ii in let rec aux b e = if e-b <= 1 then ps.(e)and here more than cp. else let m = (b+e)/2 in if ps.(m) <= cp then aux m e else aux b m in let l = Array.length ps in if l = 0 || ps.(l-1) <= cp then raise Notfound else aux 0 (l-1)

   • File: InvIndex5.ml. Time: 2.4s

   7.1.4 Imperative, linear scan

   let prev ii w cp = let cw,ps = find w ii inFor each word we add a cell with last visited occurrence. let l = Array.length ps in if l = 0 || ps.(0) >= cp then raise Notfound else if ps.(l-1) < cp then cw := l-1 else (Reset pointer if current position is not ‘‘ahead’’ of it. if !cw < l-1 && ps.(!cw+1) < cp then cw := l-1;Otherwise scan while ps.(!cw) >= cp do decr cw donestarting from last visited. ); ps.(!cw)let next ii w cp = let cw,ps = find w ii in let l = Array.length ps in if l = 0 || ps.(l-1) <= cp then raise Notfound else if ps.(0) > cp then cw := 0 else (Reset pointer if current position is not ahead of it. if !cw > 0 && ps.(!cw-1) > cp then cw := 0; while ps.(!cw) <= cp do incr cw done ); ps.(!cw)

   • End of index-building function:

     mapv (fun ps->ref 0, Array.oflist (List.rev ps)) ii,…

   • File: InvIndex6.ml

   • Time: 2.8s

   7.1.5 Imperative, galloping search

   let next ii w cp = let cw,ps = find w ii in let l = Array.length ps in if l = 0 || ps.(l-1) <= cp then raise Notfound; let rec jump (b,e as bounds) j =Locate the interval with cp inside. if e < l-1 && ps.(e) <= cp then jump (e,e+j) (2*j) else bounds in let rec binse b e =Binary search over that interval. if e-b <= 1 then e else let m = (b+e)/2 in if ps.(m) <= cp then binse m e else binse b m in if ps.(0) > cp then cw := 0 else ( let b =The invariant is that ps.(b) <= cp. if !cw > 0 && ps.(!cw-1) <= cp then !cw-1 else 0 in let b,e = jump (b,b+1) 2 inLocate interval starting near !cw. let e = if e > l-1 then l-1 else e in cw := binse b e ); ps.(!cw)

   • prev is symmetric to next.
   • File: InvIndex7.ml
   • Time: 2.4s – minimal speedup in our simple test case.

   Exercise 1.

   (Exercise 6.1 from “Modern Compiler Implementation in ML” by Andrew W. Appel.) Using the ocamlopt compiler with parameter -S and other parameters turning on all possible compiler optimizations, evaluate the compiled programs by these criteria:

   1. Are local variables kept in registers? Show on an example.
   2. If local variable b is live across more than one procedure call, is it kept in a callee-save register? Explain how it would speed up the program:let f a = let b = a+1 in let c = g () in let d = h c in b+c
   3. If local variable x is never live across a procedure call, is it properly kept in a caller-save register? Explain how doing thes would speed up the program:let h y = let x = y+1 in let z = f y in f z

   Exercise 2.

   As above, verify whether escaping variables of a function are kept in a closure corresponding to the function, or in closures corresponding to the local, i.e. nested, functions that are returned from the function (or assigned to a mutable field).

   Exercise 3.

   As above, verify that OCaml compiler performs inline expansion of small functions. Check whether the compiler can inline, or specialize (produce a local function to help inlining), recursive functions.

   Exercise 4.

   Write a “.mll program” that anonymizes, or masks, text. That is, it replaces identified probable full names (of persons, companies etc.) with fresh shorthands Mr. A, Ms. B, or Mr./Ms. C when the gender cannot be easily determined. The same (full) name should be replaced with the same letter.

   • Do only a very rough job of course, starting with recognizing two or more capitalized words in a row.

   Exercise 5.

   In the lexer EngLexer we call function abridged from the module EngMorph. Inline the operation of abridged into the lexer by adding a new regular expression pattern for each if clause. Assess the speedup on the Shakespeare corpus and the readability and either keep the change or revert it.

   Exercise 6.

   Make the lexer re-entrant for the second Menhir example (toy English grammar parser).

   Exercise 7.

   Make the determiner optional in the toy English grammar.

   1. * Can you come up with a factorization that would avoid having two more productions in total?

   Exercise 8.

   Integrate into the Phrase search example, the Porter Stemmer whose source is in the stemmer.ml file.

   Exercise 9.

   Revisit the search engine example from lecture 6.

   1. Perform optimization of data structure, i.e. replace association lists with hash tables.
   2. Optimize the algorithm: perform query optimization. Measure time gains for selected queries.
   3. For bonus points, as time and interest permits, extend the query language with OR and NOT connectives, in addition to AND.
   4. * Extend query optimization to the query language with AND, OR and NOT connectives.

   Exercise 10.

   Write an XML parser tailored to the shakespeare.xml corpus provided with the phrase search example. Modify the phrase search engine to provide detailed information for each found location, e.g. which play and who speaks the phrase.

   Lecture 10: FRP

   Zippers. Functional Reactive Programming. GUIs.

   *‘‘Zipper’‘* in Haskell Wikibook and ‘‘The Zipper’’ by Gerard Huet ‘‘How froc works’’ by Jacob Donham ‘‘The Haskell School of Expression’’ by Paul Hudak ‘‘Deprecating the Observer Pattern with Scala.React’’ by Ingo Maier, Martin Odersky

   If you see any error on the slides, let me know!

   1 Zippers

   • We would like to keep track of a position in a data structure: easily access and modify it at that location, easily move the location around.
   • Recall how we have defined context types for datatypes: types that represent a data structure with one of elements stored in it missing.

   type btree = Tip | Node of int * btree * btree

   \begin{matrix} T & = & 1 + xT^2\\\\\\ \frac{\partial T}{\partial x} & = & 0 + T^2 + 2 xT \frac{\partial T}{\partial x} = TT + 2 xT \frac{\partial T}{\partial x} \end{matrix}

   type btree_dir = LeftBranch | RightBranch
   type btree_deriv =
     | Here of btree * btree
     | Below of btree_dir * int * btree * btree_deriv

   • Location = context + subtree! But there’s a problem above.

   • But we cannot easily move the location if Here is at the bottom.

     The part closest to the location should be on top.

   • Revisiting equations for trees and lists:

     \begin{matrix} T & = & 1 + xT^2\\\\\\ \frac{\partial T}{\partial x} & = & 0 + T^2 + 2 xT \frac{\partial T}{\partial x}\\\\\\ \frac{\partial T}{\partial x} & = & \frac{T^2}{1 - 2 xT}\\\\\\ L (y) & = & 1 + yL (y)\\\\\\ L (y) & = & \frac{1}{1 - y}\\\\\\ \frac{\partial T}{\partial x} & = & T^2 L (2 xT) \end{matrix}

     I.e. the context can be stored as a list with the root as the last node.

     • Of course it doesn’t matter whether we use built-in lists, or a type with Above and Root variants.

   • Contexts of subtrees are more useful than of single elements.

     type ’a tree = Tip | Node of ’a tree * ’a * ’a treetype treedir = Leftbr | Rightbrtype ’a context = (treedir * ’a * ’a tree) listtype ’a location = {sub: ’a tree; ctx: ’a context}let access {sub} = sublet change {ctx} sub = {sub; ctx}let modify f {sub; ctx} = {sub=f sub; ctx}

   • We can imagine a location as a rooted tree, which is hanging pinned at one of its nodes. Let’s look at pictures inhttp://en.wikibooks.org/wiki/Haskell/Zippers

   • Moving around:

     let ascend loc = match loc.ctx with | [] -> locOr raise exception.| (Leftbr, n, l) :: upctx -> {sub=Node (l, n, loc.sub); ctx=upctx} | (Rightbr, n, r) :: upctx -> {sub=Node (loc.sub, n, r); ctx=upctx}let descleft loc = match loc.sub with | Tip -> locOr raise exception.| Node (l, n, r) -> {sub=l; ctx=(Rightbr, n, r)::loc.ctx}let descright loc = match loc.sub with | Tip -> locOr raise exception.| Node (l, n, r) -> {sub=r; ctx=(Leftbr, n, l)::loc.ctx}

   • Following The Zipper, let’s look at a tree with arbitrary number of branches.

   type doc = Text of string | Line | Group of doc listtype context = (doc list * doc list) listtype location = {sub: doc; ctx: context}

   let goup loc = match loc.ctx with | [] -> invalidarg “goup: at top” | (left, right) :: upctx ->Previous subdocument and its siblings.
   {sub=Group (List.rev left @ loc.sub::right); ctx=upctx}let goleft loc = match loc.ctx with | [] -> invalidarg “goleft: at top” | (l::left, right) :: upctx ->Left sibling of previous subdocument. {sub=l; ctx=(left, loc.sub::right) :: upctx} | ([], ) :: -> invalidarg “goleft: at first”

   let goright loc = match loc.ctx with | [] -> invalidarg “goright: at top” | (left, r::right) :: upctx -> {sub=r; ctx=(loc.sub::left, right) :: upctx} | (, []) :: -> invalidarg “goright: at last”let godown loc =Go to the first (i.e. leftmost) subdocument. match loc.sub with | Text -> invalidarg “godown: at text” | Line -> invalidarg “godown: at line” | Group [] -> invalidarg “godown: at empty” | Group (doc::docs) -> {sub=doc; ctx=([], docs)::loc.ctx}

   1.1 Example: Context rewriting

   • Our friend working on the string theory asked us for help with simplifying his equations.
   • The task is to pull out particular subexpressions as far to the left as we can, but changing the whole expression as little as possible.
   • We can illustrate our algorithm using mathematical notation. Let:
     • x be the thing we pull out
     • C [e] and D [e] be big expressions with subexpression e
     • operator \circ stand for one of: \ast, +
     \begin{matrix} D [(C [x] \circ e_{1}) \circ e_{2}] & \Rightarrow & D [C [x] \circ (e_{1} \circ e_{2})]\\\\\\ D [e_{2} \circ (C [x] \circ e_{1})] & \Rightarrow & D [C [x] \circ (e_{1} \circ e_{2})]\\\\\\ D [(C [x] + e_{1}) e_{2}] & \Rightarrow & D [C [x] e_{2} + e_{1} e_{2}]\\\\\\ D [e_{2} (C [x] + e_{1})] & \Rightarrow & D [C [x] e_{2} + e_{1} e_{2}]\\\\\\ D [e \circ C [x]] & \Rightarrow & D [C [x] \circ e] \end{matrix}
   • First the groundwork:

   type op = Add | Multype expr = Val of int | Var of string | App of expropexprtype exprdir = Leftarg | Rightargtype context = (exprdir * op * expr) listtype location = {sub: expr; ctx: context}

   • Locate the subexpression described by p.

   let rec findaux p e = if p e then Some (e, []) else match e with | Val | Var -> None | App (l, op, r) -> match findaux p l with | Some (sub, upctx) -> Some (sub, (Rightarg, op, r)::upctx) | None -> match findaux p r with | Some (sub, upctx) -> Some (sub, (Leftarg, op, l)::upctx) | None -> None

   let find p e = match findaux p e with | None -> None | Some (sub, ctx) -> Some {sub; ctx=List.rev ctx}

   • Pull-out the located subexpression.

   let rec pullout loc = match loc.ctx with | [] -> locDone.| (Leftarg, op, l) :: upctx ->D [e \circ C [x]] \Rightarrow D [C [x] \circ e] pullout {loc with ctx=(Rightarg, op, l) :: upctx} | (Rightarg, op1, e1) :: (, op2, e2) :: upctx when op1 = op2 ->D [(C [x] \circ e_{1}) \circ e_{2}] / D [e_{2} \circ (C [x] \circ e_{1})] \Rightarrow D [C [x] \circ (e_{1} \circ e_{2})] pullout {loc with ctx=(Rightarg, op1, App(e1,op1,e2)) :: upctx} | (Rightarg, Add, e1) :: (, Mul, e2) :: upctx -> pullout {loc with ctx=D [(C [x] + e_{1}) e_{2}] / D [e_{2} (C [x] + e_{1})] \Rightarrow D [C [x] e_{2} + e_{1} e_{2}] (Rightarg, Mul, e2) :: (Rightarg, Add, App(e1,Mul,e2)) :: upctx} | (Rightarg, op, r)::upctx ->Move up the context. pullout {sub=App(loc.sub, op, r); ctx=upctx}

   • Since operators are commutative, we ignore the direction for the second piece of context above.

   • Test:

     let (+) a b = App (a, Add, b)let ( * ) a b = App (a, Mul, b)let (!) a = Val alet x = Var “x”let y = Var “y”let ex = !5 + y * (!7 + x) * (!3 + y)let loc = find (fun e->e=x) exlet sol = match loc with | None -> raise Notfound | Some loc -> pullout loc# let = expr2str sol;;- : string = “(((xy)(3+y))+(((7y)(3+y))+5))”

   • For best results we can iterate the pull_out function until fixpoint.

   2 Adaptive Programming aka.Incremental Computing

   • Zippers are somewhat unnatural.
   • Once we change the data-structure, it is difficult to propagate the changes – need to rewrite all algorithms to work on context changes.
   • In Adaptive Programming, aka. incremental computation, aka. self-adjusting computation, we write programs in straightforward functional manner, but can later modify any data causing only minimal amount of work required to update results.
   • The functional description of computation is within a monad.
   • We can change monadic values – e.g. parts of input – from outside and propagate the changes.
     • In the Froc library, the monadic changeables are 'a Froc_sa.t, and the ability to modify them is exposed by type 'a Froc_sa.u – the writeables.

   1 Dependency Graphs (explained by Jake Dunham)

   • The monadic value 'a changeable will be the dependency graph of the computation of the represented value 'a.

   • Let’s look at the example in “How froc works”, representing computation

     let u = v / w + x * y + z

   • and its state with partial results memoized

     

     where n0, n1, n2 are interior nodes of computation.

   • Modify inputs v and z simultaneously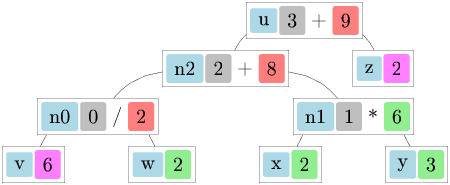

     

   • We need to update n2 before u.

   • We use the gray numbers – the order of computation – for the order of update of n0, n2 and u.

   • Similarly to parallel in the concurrency monad, we provide bind2, bind3, … – and corresponding lift2, lift3, … – to introduce nodes with several children.

     let n0 = bind2 v w (fun v w -> return (v / w)) let n1 = bind2 x y (fun x y -> return (x * y)) let n2 = bind2 n0 n1 (fun n0 n1 -> return (n0 + n1)) let u = bind2 n2 z (fun n2 z -> return (n2 + z))

   • Do-notation is not necessary to have readable expressions.

     let (/) = lift2 (/) let ( * ) = lift2 ( * ) let (+) = lift2 (+) let u = v / w + x * y + z

   • As in other monads, we can decrease overhead by using bigger chunks.

     let n0 = blift2 v w (fun v w -> v / w) let n2 = blift3 n0 x y (fun n0 x y -> n0 + x * y) let u = blift2 n2 z (fun n2 z -> n2 + z)

   • We have a problem if we recompute all nodes by order of computation.

     let b = x >>= fun x -> return (x = 0) let n0 = x >>= fun x -> return (100 / x) let y = bind2 b n0 (fun b n0->if b then return 0 else n0)

     

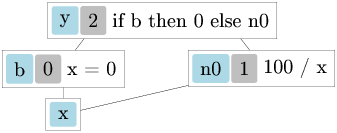
   • Rather than a signle “time” stamp, we store intervals: begin and end of computation

     

   • When updating the y node, we first detach nodes in range 4-9 from the graph.

     • Computing the expression will re-attach the nodes as needed.

   • When value of b does not change, then we skip updating y and proceed with updating n0.

     • I.e. no children of y with time stamp smaller than y change.
     • The value of y is a link to the value of n0 so it will change anyway.

   • We need memoization to re-attach the same nodes in case they don’t need updating.

     • Are they up-to-date? Run updating past the node’s timestamp range.

   2.1 Example using Froc

   • Download Froc from https://github.com/jaked/froc/downloads

   • Install for example with

     cd froc-0.2a; ./configure; make all; sudo make install

   • Frocsa (for self-adjusting) exports the monadic type t for changeable computation, and a handle type u for updating the computation.

   • open Frocsatype tree =Binary tree with nodes storing their screen location.| Leaf of int * intWe will grow the tree| Node of int * int * tree t * tree tby modifying subtrees.

   • let rec display px py t =Displaying the tree is changeable effect: match t withwhenever the tree changes, displaying will be updated. | Leaf (x,

     25. ->Only new nodes will be drawn after update. return
         (Graphics.drawpolyline [|px,py;x,y|];We return Graphics.drawcircle x y 3)a throwaway value. | Node (x, y, l, r) -> return (Graphics.drawpolyline [|px,py;x,y|]) >>= fun -> l >>= display x y >>= fun -> r >>= display x y

   • let growat (x, depth, upd) = let xl = x-f2i (width.(2.0(\sim-.(i2f (depth+1))))) in let l, updl = changeable (Leaf (xl, (depth+1)20)) in
     let xr = x+f2i (width.(2.0(\sim-.(i2f (depth+1))))) in let r, updr = changeable (Leaf (xr, (depth+1)20)) in write upd (Node (x, depth*20, l, r));Update the old leaf propagate ();and keep handles to make future updates. [xl, depth+1, updl; xr, depth+1, updr]

   • let rec loop t subts steps = if steps <= 0 then () else loop t (concatmap growat subts) (steps-1)let incremental steps () =
     Graphics.opengraph ” 1024x600”; let t, u = changeable (Leaf (512, 20)) in
     let d = t >>= display (f2i (width /. 2.)) 0 inDisplay once loop t [512, 1, u] steps;– new nodes will be drawn automatically.
     Graphics.closegraph ();;

   • Compare with rebuilding and redrawing the whole tree. Unfortunately the overhead of incremental computation is quite large. Byte code run:

     depth	12	13	14	15	16	17	18	19	20
     incremental	0.66s	1s	2.2s	4.4s	9.3s	21s	50s	140s	255s
     rebuilding	0.5s	0.63s	1.3s	3s	5.3s	13s	39s	190s

   3 Functional Reactive Programming

   • FRP is an attempt to declaratively deal with time.

   • Behaviors are functions of time.

     • A behavior has a specific value in each instant.

   • Events are sets of (time, value) pairs.

     • I.e. they are organised into streams of actions.

   • Two problems

     • Behaviors / events are well defined when they don’t depend on future
     • Efficiency: minimize overhead

   • FRP is synchronous: it is possible to set up for events to happen at the same time, and it is continuous: behaviors can have details at arbitrary time resolution.

     • Although the results are sampled, there’s no fixed (minimal) time step for specifying behavior.
     • Asynchrony refers to various ideas so ask what people mean.

   • Ideally we would define:

     type time = floattype ’a behavior = time -> ’aArbitrary function.type ’a event = (’a, time) streamIncreasing time instants.

   • Forcing a lazy list (stream) of events would wait till an event arrives.

   • But behaviors need to react to external events:

     type useraction =| Key of char * bool| Button of int * int * bool * bool| MouseMove of int * int| Resize of int * inttype ’a behavior = useraction event -> time -> ’a

   • Scanning through an event list since the beginnig of time till current time, each time we evaluate a behavior – very wasteful wrt. time&space.

     Producing a stream of behaviors for the stream of time allows to forget about events already in the past.

     type ’a behavior = useraction event -> time stream -> ’a stream

   • Next optimization is to pair user actions with sampling times.

     type ’a behavior = (useraction option * time) stream -> ’a stream

     None action corresponds to sampling time when nothing happens.

   • Turning behaviors and events from functions of time into input-output streams is similar to optimizing interesction of ordered lists from O (mn) to O (m + n) time.

   • Now we can in turn define events in terms of behaviors:

     type ’a event = ’a option behavior

     although it betrays the discrete character of events (happening at points in time rather than varying over intervals of time).

   • We’ve gotten very close to stream processing as discussed in lecture 7.

     • Recall the incremental pretty-printing example that can “react” to more input.
     • Stream combinators, fork from exercise 9 for lecture 7, and a corresponding merge, turn stream processing into synchronous discrete reactive programming.

   • Behaviors are monadic (but see next point) – in original specification:

     type ’a behavior = time -> ’aval return : ’a -> ’a behaviorlet return a = fun -> aval bind : ’a behavior -> (’a -> ’b behavior) -> ’b behaviorlet bind a f = fun t -> f (a t) t

   • As we’ve seen with changeables, we mostly use lifting. In Haskell world we’d call behaviors applicative. To build our own lifters in any monad:

     val ap : (’a -> ’b) monad -> ’a monad -> ’b monadlet ap fm am = perform f <– fm; a <– am; return (f a)

     • Note that for changeables, the naive implementation above will introduce unnecessary dependencies. Monadic libraries for incremental computing or FRP should provide optimized variants if needed.
       • Compare with parallel for concurrent computing.

   • Going from events to behaviors. until and switch have type

     ’a behavior -> ’a behavior event -> ’a behavior

     step has type

     ’a -> ’a event -> ’a behavior

     • until b es behaves as b until the first event in es, then behaves as the behavior in that event
     • switch b es behaves as the behavior from the last event in es prior to current time, if any, otherwise as b
     • step a b starts with behavior returning a and then switches to returning the value of the last event in b (prior to current time) – a step function.

   • We will use “signal” to refer to a behavior or an event. But often “signal” is used as our behavior (check terminology when looking at a new FRP library).

   4 Reactivity by Stream Processing

   • The stream processing infrastructure should be familiar.

     type ’a stream = ’a stream Lazy.tand ’a stream = Cons of ’a * ’a streamlet rec lmap f l = lazy ( let Cons (x, xs) = Lazy.force l in Cons (f x, lmap f xs))let rec liter (f : ’a -> unit) (l : ’a stream) : unit = let Cons (x, xs) = Lazy.force l in f x; liter f xslet rec lmap2 f xs ys = lazy (
     let Cons (x, xs) = Lazy.force xs in let Cons (y, ys) = Lazy.force ys in
     Cons (f x y, lmap2 f xs ys))let rec lmap3 f xs ys zs = lazy ( let Cons (x, xs) = Lazy.force xs in let Cons (y, ys) = Lazy.force ys in let Cons (z, zs) = Lazy.force zs in Cons (f x y z, lmap3 f xs ys zs))let rec lfold acc f (l : ’a stream) = lazy ( let Cons (x, xs) = Lazy.force l inFold a function over the stream let acc = f acc x inproducing a stream of partial results.
     Cons (acc, lfold acc f xs))

   • Since a behavior is a function of user actions and sample times, we need to ensure that only one stream is created for the actual input stream.

     type (‘a, ’b) memo1 = {memof : ’a -> ’b; mutable memor : (’a * ’b) option}let memo1 f = {memof = f; memor = None}let memo1app f x = match f.memor with | Some (y, res) when x == y -> resPhysical equality is OK –| ->external input is ‘‘physically’’ unique. let res = f.memof x inWhile debugging, we can monitor f.memor <- Some (x, res);whether f.memor = None before. reslet ($) = memo1apptype ’a behavior =
     ((useraction option * time) stream, ’a stream) memo1

   • The monadic/applicative functions to build complex behaviors.

     • If you do not provide type annotations in .ml files, work together with an .mli file to catch problems early. You can later add more type annotations as needed to find out what’s wrong.

     let returnB x : ’a behavior = let rec xs = lazy (Cons (x, xs)) in memo1 (fun -> xs)let ( !* ) = returnBlet liftB f fb = memo1 (fun uts -> lmap f (fb $ uts))let liftB2 f fb1 fb2 = memo1 (fun uts -> lmap2 f (fb1 $ uts) (fb2 $ uts))let liftB3 f fb1 fb2 fb3 = memo1 (fun uts -> lmap3 f (fb1 $ uts) (fb2 $ uts) (fb3 $ uts))let liftE f (fe : ’a event) : ’b event = memo1 (fun uts -> lmap (function Some e -> Some (f e) | None -> None) (fe $ uts))let (=>>) fe f = liftE f felet (->>) e v = e =>> fun -> v

   • Creating events out of behaviors.

     let whileB (fb : bool behavior) : unit event = memo1 (fun uts ->
     lmap (function true -> Some () | false -> None) (fb $ uts))let unique fe : ’a event = memo1 (fun uts -> let xs = fe $ uts in
     lmap2 (fun x y -> if x = y then None else y) (lazy (Cons (None, xs))) xs)let whenB fb = memo1 (fun uts -> unique (whileB fb) $ uts)let snapshot fe fb : (’a * ’b) event = memo1 (fun uts -> lmap2 (fun x->function Some y -> Some (y,x) | None -> None) (fb $ uts) (fe $ uts))

   • Creating behaviors out of events.

     let step acc fe =The step function: value of last event. memo1 (fun uts -> lfold acc (fun acc -> function None -> acc | Some v -> v) (fe $ uts))let stepaccum acc ff =Transform a value by a series of functions. memo1 (fun uts -> lfold acc (fun acc -> function | None -> acc | Some f -> f acc) (ff $ uts))

   • To numerically integrate a behavior, we need to access the sampling times.

     let integral fb = let rec loop t0 acc uts bs = let Cons ((,t1), uts) = Lazy.force uts in let Cons (b, bs) = Lazy.force bs in let acc = acc +. (t1 -. t0) *. b inb =\operatorname{fb} (t_{1}), \operatorname{acc} \approx \int_{t \leqslant t_{0}} f. Cons (acc, lazy (loop t1 acc uts bs)) in memo1 (fun uts -> lazy ( let Cons ((,t), uts’) = Lazy.force uts in Cons (0., lazy (loop t 0. uts’ (fb $ uts)))))

     • In our paddle game example, we paradoxically express position and velocity in mutually recursive manner. The trick is the same as in chapter 7 – integration introduces one step of delay.

   • User actions:

     let lbp : unit event = memo1 (fun uts -> lmap (function Some(Button(,)), -> Some() | -> None) uts)let mm : (int * int) event = memo1 (fun uts -> lmap (function Some(MouseMove(x,y)), ->Some(x,y) | ->None) uts)let screen : (int * int) event = memo1 (fun uts -> lmap (function Some(Resize(x,y)), ->Some(x,y) | ->None) uts)let mousex : int behavior = step 0 (liftE fst mm)let mousey : int behavior = step 0 (liftE snd mm)let width : int behavior = step 640 (liftE fst screen)let height : int behavior = step 512 (liftE snd screen)

   1 The Paddle Game example

   • A scene graph is a data structure that represents a “world” which can be drawn on screen.

     type scene =| Rect of int * int * int * intposition, width, height| Circle of int * int * intposition, radius| Group of scene list| Color of Graphics.color * scenecolor of subscene objects|Translate of float * float * sceneadditional offset of origin

   • Drawing a scene explains what we mean above.

     let draw sc = let f2i = intoffloat in let open Graphics in let rec aux tx ty = functionAccumulate translations. | Rect (x, y, w, h) ->
     fillrect (f2i tx+x) (f2i ty+y) w h | Circle (x, y, r) -> fillcircle (f2i tx+x) (f2i ty+y) r | Group scs -> List.iter (aux tx ty) scs\swarrow Set color for sc objects.| Color (c, sc) -> setcolor c; aux tx ty sc | Translate (x, y, sc) -> aux (tx+.x) (ty+.y) sc in
     cleargraph ();‘‘Fast and clean’’ removing of previous picture. aux 0. 0. sc; synchronize ()Synchronize the double buffer – avoiding flickering.

   • An animation is a scene behavior. To animate it we need to create the input stream: the user actions and sampling times stream.

     • We could abstract away drawing from time sampling in reactimate, asking for (i.e. passing as argument) a producer of user actions and a consumer of scene graphs (like draw).

     let reactimate (anim : scene behavior) = let open Graphics in let notb = function Some (Button (,)) -> false | -> true in let current oldm oldscr (oldu, t0) = let rec delay () = let t1 = Unix.gettimeofday () in let d = 0.01 -. (t1 -. t0) in try if d > 0. then Thread.delay d; Unix.gettimeofday () with Unix.Unixerror (( Unix.EAGAIN ), , ) -> delay () in let t1 = delay () in let s = Graphics.waitnextevent [Poll] in let x = s.mousex and y = s.mousey and scrx = Graphics.sizex () and scry = Graphics.sizey () in let ue = if s.keypressed then Some (Key s.key) else if (scrx, scry) <> oldscr then Some (Resize (scrx,scry)) else if s.button && notb oldu then Some (Button (x, y)) else if (x, y) <> oldm then Some (MouseMove (x, y)) else None in (x, y), (scrx, scry), (ue, t1) in opengraph ““;Open window. displaymode false;Draw using double buffering. let t0 = Unix.gettimeofday () in let rec utstep mpos scr ut = lazy ( let mpos, scr, ut = current mpos scr ut in Cons (ut, utstep mpos scr ut)) in let scr = Graphics.sizex (), Graphics.sizey () in let ut0 = Some (Resize (fst scr, snd scr)), t0 in liter draw (anim $ lazy (Cons (ut0, utstep (0,0) scr ut0))); closegraph ()Close window – unfortunately never happens.

   • General-purpose behavior operators.

     let (+) = liftB2 (+)let (-) = liftB2 (-)let ( *** ) = liftB2 ( * )let (/) = liftB2 (/)let (&&) = liftB2 (&&)let (||) = liftB2 (||)let (<) = liftB2 (<)let (>*) = liftB2 (>)

   • The walls are drawn on left, top and right borders of the window.

     let walls = liftB2 (fun w h -> Color (Graphics.blue, Group [Rect (0, 0, 20, h-1); Rect (0, h-21, w-1, 20); Rect (w-21, 0, 20, h-1)]))
     width height

   • The paddle is tied to the mouse at the bottom border of the window.

     let paddle = liftB (fun mx -> Color (Graphics.black, Rect (mx, 0, 50, 10))) mousex

   • The ball has a velocity in pixels per second. It bounces from the walls, which is hard-coded in terms of distance from window borders.

     • Unfortunately OCaml, being an eager language, does not let us encode recursive behaviors in elegant way. We need to unpack behaviors and events as functions of the input stream.
     • xbounce ->> (\sim-.) event is just the negation function happening at each horizontal bounce.
     • stepaccum vel (xbounce ->> (\sim-.)) behavior is vel value changing sign at each horizontal bounce.
     • liftB intoffloat (integral xvel) +* width /* !*2 – first integrate velocity, then truncate it to integers and offset to the middle of the window.
     • whenB ((xpos >* width -* !27) || (xpos <* !*27)) – issue an event the first time the position exceeds the bounds. This ensures there are no further bouncings until the ball moves out of the walls.

   let pbal vel = let rec xvel uts = stepaccum vel (xbounce ->> (\sim-.)) $ uts and xvel = {memof = xvel; memor = None} and xpos uts = (liftB intoffloat (integral xvel) +* width /* !2) $ uts and xpos = {memof = xpos; memor = None} and xbounce uts = whenB ((xpos > width -* !27) || (xpos <* !27)) $ uts and xbounce = {memof = xbounce; memor = None} in let rec yvel uts = (stepaccum vel (ybounce ->> (\sim-.))) $ uts and yvel = {memof = yvel; memor = None} and ypos uts = (liftB intoffloat (integral yvel) + height /* !2) $ uts and ypos = {memof = ypos; memor = None} and ybounce uts = whenB ( (ypos > height -* !27) || ((ypos <* !17) && (ypos >* !7) && (xpos >* mousex) &&* (xpos <* mousex +* !*50))) $ uts and ybounce = {memof = ybounce; memor = None} in liftB2 (fun x y -> Color (Graphics.red, Circle (x, y, 6))) xpos ypos

   • Invocation:

     ocamlbuild Lec10b.native -cflags -I,+threads -libs graphics,unix,threads/threads --

   • 

   5 Reactivity by Incremental Computing

   • In Froc behaviors and events are both implemented as changeables but only behaviors persist, events are “instantaneous”.
     • Behaviors are composed out of constants and prior events, capture the “changeable” aspect.
     • Events capture the “writeable” aspect – after their values are propagated, the values are removed.
     Events and behaviors are called signals.
   • Froc does not represent time, and provides the function changes : ’a behavior -> ’a event, which violates the continuous semantics we introduced before.
     • It breaks the illusion that behaviors vary continuously rather than at discrete points in time.
     • But it avoids the need to synchronize global time samples with events in the system. It is “less continuous but more dense”.
   • Sending an event – send – starts an update cycle. Signals cannot call send, but can send_deferred which will send an event in next cycle.
     • Things that happen in the same update cycle are simultaneous.
     • Events are removed (detached from dependency graph) after an update cycle.
   • Froc provides the fix_b, fix_e functions to define signals recursively. Current value refers to value from previous update cycle, and defers next recursive step to next cycle, until convergence.
   • Update cycles can happen “back-to-back” via send_deferred and fix_b, fix_e, or can be invoked from outside Froc by sending events at arbitrary times.
     • With a time behavior that holds a clock event value, events from “back-to-back” update cycles can be at the same clock time although not simultaneous in this sense.
     • Update cycles prevent glitches, where outdated signal is used e.g. to issue an event.
   • Let’s familiarize ourselves with Froc API:http://jaked.github.com/froc/doc/Froc.html
   • A behavior is written in pure style, when its definition does not use send, send_deferred, notify_e, notify_b and sample:
     • sample, notify_e, notify_b are used from outside the behavior (from its “environment”) analogously to observing result of a function,
     • send, send_deferred are used from outside analogously to providing input to a function.
   • We will develop an example in a pragmatic, impure style, but since purity is an important aspect of functional programming, I propose to rewrite it in pure style as an exercise (ex. 5).
   • When writing in impure style we need to remember to refer from somewhere to all the pieces of our behavior, otherwise the unreferred parts will be garbage collected breaking the behavior.
     • A value is referred to, when it has a name in the global environment or is part of a bigger value that is referred to (for example it’s stored somewhere). Signals can be referred to by being part of the dependency graph, but also by any of the more general ways.

   1 Reimplementing the Paddle Game example

   • Rather than following our incremental computing example (a scene with changeable parts), we follow our FRP example: a scene behavior.

   • First we introduce time:

     open Froclet clock, tick = makeevent ()let time = hold (Unix.gettimeofday ()) clock

   • Next we define integration:

     let integral fb = let aux (sum, t0) t1 = sum +. (t1 -. t0) *. sample fb, t1 in collectb aux (0., sample time) clock

     For convenience, the integral remembers the current upper limit of integration. It will be useful to get the integer part:

     let integres fb = lift (fun (v,) -> intoffloat v) (integral fb)

   • We can also define integration in pure style:

     let pair fa fb = lift2 (fun x y -> x, y) fa fblet integralnice fb = let samples = changes (pair fb time) in let aux (sum, t0) (fv, t1) = sum +. (t1 -. t0) *. fv, t1 in collectb aux (0., sample time) samples

     The initial value (0., sample time) is not “inside” the behavior so sample here does not spoil the pure style.

   • The scene datatype and how we draw a scene does not change.

   • Signals which will be sent to behaviors:

     let mousemovex, movemousex = makeevent ()let mousemovey, movemousey = makeevent ()let mousex = hold 0 mousemovexlet mousey = hold 0 mousemovexlet widthresized, resizewidth = makeevent ()let heightresized, resizeheight = makeevent ()let width = hold 640 widthresizedlet height = hold 512 heightresizedlet mbuttonpressed, pressmbutton = makeevent ()let keypressed, presskey = makeevent ()

   • The user interface main loop, emiting signals and observing behaviors:

     let reactimate (anim : scene behavior) = let open Graphics in let rec loop omx omy osx osy omb t0 = let rec delay () = let t1 = Unix.gettimeofday () in let d = 0.01 -. (t1 -. t0) in try if d > 0. then Thread.delay d; Unix.gettimeofday () with Unix.Unixerror ((* Unix.EAGAIN *), , ) -> delay () in let t1 = delay () in let s = Graphics.waitnextevent [Poll] in let x = s.mousex and y = s.mousey and scrx = Graphics.sizex () and scry = Graphics.sizey () in if s.keypressed then send presskey s.key;We can send signals if scrx <> osx then send resizewidth scrx;one by one. if scry <> osy then send resizeheight scry; if s.button && not omb then send pressmbutton (); if x <> omx then send movemousex x; if y <> omy then send movemousey y; send tick t1; draw (sample anim);After all signals are updated, observe behavior. loop x y scrx scry s.button t1 in opengraph ““; displaymode false; loop 0 0 640 512 false (Unix.gettimeofday ()); closegraph ()

   • The simple behaviors as in Lec10b.ml. Pragmatic (impure) bouncing:

     let pbal vel =  let xbounce, bouncex = makeevent () in  let ybounce, bouncey 
     =
     makeevent () in  let xvel = collectb (fun v  -> $\sim$-.v) vel xbounce
     in  let yvel = collectb (fun v  -> $\sim$-.v) vel ybounce in  let xpos =
     integres xvel +* width /* !*2 in  let ypos = integres yvel +* height /*
     !*2 in  let xbounce = whentrue    ((xpos >* width -* !*27) ||*
     (xpos <* !*27)) in  notifye xbounce (send bouncex);  let ybounce =
     whentrue (    (ypos >* height -* !*27) ||*      ((ypos <*
     !*17) &&* (ypos >* !*7) &&*          (xpos >* mousex) &&*
     (xpos <* mousex +* !*50))) in  notifye ybounce (send bouncey);
     lift4 (fun x y   -> Color (Graphics.red, Circle (x, y, 6)))    xpos ypos
     (hold () xbounce) (hold () ybounce)

   • We hold on to xbounce and ybounce above to prevent garbage collecting them. We could instead remember them in the “toplevel”:

     let pbal vel = … xbounce, ybounce, lift2 (fun x y -> Color (Graphics.red, Circle (x, y, 6))) xpos yposlet xb, yb, ball = pbal 100.let game = lift3 (fun walls paddle ball -> Group [walls; paddle; ball]) walls paddle ball

   • We can easily monitor signals while debugging, e.g.:

     notifye xbounce (fun () -> Printf.printf “xbounce%!”); notifye ybounce (fun () -> Printf.printf “ybounce%!”);

   • Invocation:ocamlbuild Lec10c.native -cflags -I,+froc,-I,+threads -libs froc/froc,unix,graphics,threads/threads --

   6 Direct Control

   • Real-world behaviors often are state machines, going through several stages. We don’t have declarative means for it yet.

     • Example: baking recipes. 1. Preheat the oven. 2. Put flour, sugar, eggs into a bowl. 3. Spoon the mixture. etc.

   • We want a flow to be able to proceed through events: when the first event arrives we remember its result and wait for the next event, disregarding any further arrivals of the first event!

     • Therefore Froc constructs like mapping an event: map, or attaching a notification to a behavior change: bind b1 (fun v1 -> notify_b ~now:false b2 (fun v2 -> …)), will not work.

   • We also want to be able to repeat or loop a flow, but starting from the notification of the first event that happens after the notification of the last event.

   • next e is an event propagating only the first occurrence of e. This will be the basis of our await function.

   • The whole flow should be cancellable from outside at any time.

   • A flow is a kind of a lightweight thread as in end of lecture 8, we’ll make it a monad. It only “stores” a non-unit value when it awaits an event. But it has a primitive to emit values.

     • We actually implement coarse-grained threads (lecture 8 exercise 11), with await in the role of suspend.

   • We build a module Flow with monadic type (’a, ’b) flow “storing” 'b and emitting 'a.

     type (’a, ’b) flowtype cancellableA handle to cancel a flow (stop further computation).val noopflow : (’a, unit) flowSame as return ().val return : ’b -> (’a, ’b) flowCompleted flow.val await : ’b Froc.event -> (’a, ’b) flowWait and store event:val bind :the principled way to input. (’a, ’b) flow -> (’b -> (’a, ’c) flow) -> (’a, ’c) flowval emit : ’a -> (’a, unit) flowThe principled way to output.val cancel : cancellable -> unitval repeat :Loop the given flow and store the stop event. ?until:’a Froc.event -> (’b, unit) flow -> (’b, ’a) flowval eventflow : (’a, unit) flow -> ’a Froc.event * cancellableval behaviorflow :The initial value of a behavior and a flow to update it.
     ’a -> (’a, unit) flow -> ’a Froc.behavior * cancellableval iscancelled : cancellable -> bool

   • We follow our (or Lwt) implementation of lightweight threads, adapting it to the need of cancelling flows.

     module F = Froctype ’a result =| Return of 'a\downarrowNotifications to cancel when cancelled.| Sleep of (’a -> unit) list * F.cancel ref list| Cancelled| Link of ’a stateand ’a state = {mutable state : ’a result}type cancellable = unit state

   • Functions find, wakeup, connect are as in lecture 8 (but connecting to cancelled thread cancels the other thread).

   • Our monad is actually a reader monad over the result state. The reader supplies the emit function. (See exercise 10.)

     type (’a, ’b) flow = (’a -> unit) -> ’b state

   • The return and bind functions are as in our lightweight threads, but we need to handle cancelled flows: for m = bind a b, if a is cancelled then m is cancelled, and if m is cancelled then don’t wake up b:

       let waiter x =        if not (iscancelled m)        then connect m (b 

     x emit) in …

   • await is implemented like next, but it wakes up a flow:

     let await t = fun emit -> let c = ref F.nocancel in let m = {state=Sleep ([], [c])} in c := F.notifyecancel t begin fun r ->
     F.cancel !c; c := F.nocancel; wakeup m r end; m

   • repeat attaches the whole loop as a waiter for the loop body.

     let repeat ?(until=F.never) fa = fun emit -> let c = ref F.nocancel in let out = {state=Sleep ([], [c])} in let cancelbody = ref {state=Cancelled} in c := F.notifyecancel until begin fun tv ->
     F.cancel !c; c := F.nocancel; Exiting the loop consists of cancelling the loop body cancel !cancelbody; wakeup out tvand waking up loop waiters.end; let rec loop () = let a = find (fa emit) in cancelbody := a; (match a.state with | Cancelled -> cancel out; F.cancel !c | Return x -> failwith “loopuntil: not implemented for unsuspended flows” | Sleep (xwaiters, xcancels) -> a.state <- Sleep (loop::xwaiters, xcancels)
     | Link -> assert false) in loop (); out

   • Example: drawing shapes. Invocation:ocamlbuild Lec10d.native -pp "camlp4o monad/pa_monad.cmo" -libs froc/froc,graphics -cflags -I,+froc --

   • The event handlers and drawing/event dispatch loop reactimate is similar to the paddle game example (we removed unnecessary events).

   • The scene is a list of shapes, the first shape is open.

     type scene = (int * int) list listlet draw sc = let open Graphics in
     cleargraph (); (match sc with | [] -> () | opn::cld ->
     drawpolyline (Array.oflist opn); List.iter (fillpoly -| Array.oflist) cld); synchronize ()

   • We build a flow and turn it into a behavior to animate.

     let painter = let cld = ref [] inGlobal state of painter. repeat (perform
     await mbuttonpressed;Start when button down. let opn = ref [] in
     repeat (perform mpos <– await mousemove;\swarrowAdd next position to line. emit (opn := mpos :: !opn; !opn :: !cld))
     \simuntil:mbuttonreleased;\swarrowStart new shape. emit (cld := !opn :: !cld; opn := []; [] :: !cld))let painter, cancelpainter = behaviorflow [] painterlet () = reactimate painter

   • 

   1 Flows and state

   Global state and thread-local state can be used with lightweight threads, but pay attention to semantics – which computations are inside the monad and which while building the initial monadic value.

   • Side effects hidden in return and emit arguments are not inside the monad. E.g. if in the “first line” of a loop effects are executed only at the start of the loop – but if after bind (“below first line” of a loop), at each step of the loop.

   let f = repeat (perform emit (Printf.printf “[0]%!”; ‘0’); () <– await aas; emit (Printf.printf “[1]%!”; ‘1’); () <– await bs; emit (Printf.printf “[2]%!”; ‘2’); () <– await cs; emit (Printf.printf “[3]%!”; ‘3’); () <– await ds; emit (Printf.printf “[4]%!”; ‘4’))let e, cancele = eventflow flet () = F.notifye e (fun c -> Printf.printf “flow: %c%!” c); Printf.printf “notification installed%!”let () = F.send a (); F.send b (); F.send c (); F.send d (); F.send a (); F.send b (); F.send c (); F.send d ()

   [0]Only printed once – when building the loop.notification installedOnly installed after the first flow event sent.event: aEvent notification (see source Lec10e.ml).[1]Second emit computed after first await returns.flow: 1Emitted signal.event: bNext event…[2]flow: 2event: c[3]flow: 3event: d[4]flow: 4Last signal emitted from first turn of the loop –flow: 0and first signal of the second turn (but [0] not printed).event: a[1]flow: 1event: b[2]flow: 2event: c[3]flow: 3event: d[4]flow: 4flow: 0Program ends while flow in third turn of the loop.

   7 Graphical User Interfaces

   • In-depth discussion of GUIs is beyond the scope of this course. We only cover what’s needed for an example reactive program with direct control.
   • Demo of libraries LablTk based on optional labelled arguments discussed in lecture 2 exercise 2, and polymorphic variants, and LablGtk additionally based on objects. We will learn more about objects and polymorphic variants in next lecture.

   7.1 Calculator Flow

   let digits, digit = F.makeevent ()We represent the mechanicslet ops, op = F.makeevent ()of the calculator directly as a flow.let dots, dot = F.makeevent ()let calc =We need two state variables for two arguments of calculation let f = ref (fun x -> x) and now = ref 0.0 inbut we repeat (performremember the older argument in partial application. op <– repeat
   (performEnter the digits of a number (on later turns d <– await digits;starting from the second digit) emit (now := 10. *. !now +. d; !now)) \simuntil:ops;until operator button is pressed.
   emit (now := !f !now; f := op !now; !now); d <– repeat\nwarrowCompute the result and ‘‘store away’’ the operator.(perform op <– await ops; return (f := op !now)) \simuntil:digits;The user can pick a different operator. emit (now := d; !now))Reset the state to a new number.let calce, cancelcalc = eventflow calcNotifies display update.

   7.2 Tk: LablTk

   • Widget toolkit Tk known from the Tcl language.

   • Invocation:ocamlbuild Lec10tk.byte -cflags -I,+froc -libs froc/froc -pkg labltk -pp "camlp4o monad/pa_monad.cmo" --

     • For unknown reason I had build problems with ocamlopt (native).

   • Layout of the calculator – common across GUIs.

     let layout = [|[|“7”,’Di 7.; “8”,’Di 8.; “9”,’Di 9.; “+”,’O (+.)|];
     [|“4”,’Di 4.; “5”,’Di 5.; “6”,’Di 6.; “-”,’O (-.)|]; [|“1”,’Di 1.; “2”,’Di 2.; “3”,’Di 3.; ““,’O ( .)|]; [|“0”,’Di 0.; “.”,’Dot; “=”, ’O sk; “/”,’O (/.)|]|]

   • Every widget (window gadget) has a parent in which it is located.

   • Buttons have action associated with pressing them, labels just provide information, entries (aka. edit fields) are for entering info from keyboard.

     • Actions are callback functions passed as the \simcommand argument.

   • Frames in Tk group widgets.

   • The parent is sent as last argument, after optional labelled arguments.

     let top = Tk.openTk ()let btnframe = Frame.create \simrelief:’Groove \simborderwidth:2 toplet buttons = Array.map (Array.map (function | text, ’Dot -> Button.create \simtext \simcommand:(fun () -> F.send dot ()) btnframe | text, ’Di d -> Button.create \simtext \simcommand:(fun () -> F.send digit d) btnframe | text, ’O f -> Button.create \simtext \simcommand:(fun () -> F.send op f) btnframe)) layoutlet result = Label.create \simtext:“0” \simrelief:’Sunken top

   • GUI toolkits have layout algorithms, so we only need to tell which widgets hang together and whether they should fill all available space etc. – via pack, or grid for “rectangular” organization.

   • \simfill: the allocated space in ‘X, ‘Y, ‘Both or ‘None axes;\simexpand: maximally how much space is allocated or only as needed.

   • \simanchor: allows to glue a widget in particular direction (‘Center, ‘E, ‘Ne etc.)

   • The grid packing flexibility: \simcolumnspan and \simrowspan.

   • configure functions accept the same arguments as create but change existing widgets.

   • let () = Wm.titleset top “Calculator”; Tk.pack [result] \simside:’Top \simfill:’X; Tk.pack [btnframe] \simside:’Bottom \simexpand:true;
     Array.iteri (fun column ->Array.iteri (fun row button -> Tk.grid \simcolumn \simrow [button])) buttons; Wm.geometryset top “200x200”;
     F.notifye calce (fun now -> Label.configure \simtext:(stringoffloat now) result); Tk.mainLoop ()

   • 

   7.3 GTk+: LablGTk

   • LablGTk is build as an object-oriented layer over a low-level layer of functions interfacing with the GTk+ library, which is written in C.

   • In OCaml, object fields are only visible to object methods, and methods are called with # syntax, e.g. window#show ()

   • The interaction with the application is reactive:

     • Our events are called signals in GTk+.
     • Registering a notification is called connecting a signal handler, e.g.button#connect#clicked \simcallback:hello which takes \sim {\nobreak}callback:(unit -> unit) and returns GtkSignal.id.
       • As with Froc notifications, multiple handlers can be attached.
     • GTk+ events are a subclass of signals related to more specific window events, e.g.window#event#connect#delete \simcallback:deleteevent
     • GTk+ event callbacks take more info: \simcallback:(event -> unit) for some type event.

   • Automatic layout (aka. packing) seems less sophisticated than in Tk:

     • only horizontal and vertical boxes,
     • therefore \simfill is binary and \simanchor is replaced by \simfrom ‘START or ‘END.

   • Automatic grid layout is called table.

     • \simfill and \simexpand take ‘X, ‘Y, ‘BOTH, ‘NONE.

   • The coerce method casts the type of the object (in Tk there is coe function).

   • Labels don’t have a dedicated module – see definition of result widget.

   • Widgets have setter methods widget#set_X (instead of a single configure function in Tk).

   • Invocation:ocamlbuild Lec10gtk.native -cflags -I,+froc -libs froc/froc -pkg lablgtk2 -pp "camlp4o monad/pa_monad.cmo" --

   • The model part of application doesn’t change.

   • Setup:

     let = GtkMain.Main.init ()let window = GWindow.window \simwidth:200 \simheight:200 \simtitle:“Calculator” ()let top = GPack.vbox \simpacking:window#add ()let result = GMisc.label \simtext:“0” \simpacking:top#add ()let btnframe = GPack.table \simrows:(Array.length layout) \simcolumns:(Array.length layout.(0)) \simpacking:top#add ()

   • Button actions:

     let buttons = Array.map (Array.map (function | label, ’Dot -> let b = GButton.button \simlabel () in let = b#connect#clicked
     \simcallback:(fun () -> F.send dot ()) in b | label, ’Di d ->
     let b = GButton.button \simlabel () in let = b#connect#clicked
     \simcallback:(fun () -> F.send digit d) in b | label, ’O f ->
     let b = GButton.button \simlabel () in let = b#connect#clicked
     \simcallback:(fun () -> F.send op f) in b)) layout

   • Button layout, result notification, start application:

     let deleteevent = GMain.Main.quit (); falselet () = let = window#event#connect#delete \simcallback:deleteevent in Array.iteri (fun column->Array.iteri (fun row button -> btnframe#attach \simleft:column \simtop:row \simfill:’BOTH \simexpand:’BOTH (button#coerce)) ) buttons; F.notifye calce (fun now -> result#setlabel (stringoffloat now)); window#show (); GMain.Main.main ()

   • 

   Functional Programming

   Zippers, Reactivity, GUIs

   Exercise 1: Introduce operators -, / into the context rewriting “pull out subexpression” example. Remember that they are not commutative.

   Exercise 2: Add to the paddle game example:

   1. game restart,
   2. score keeping,
   3. game quitting (in more-or-less elegant way).

   Exercise 3: Our numerical integration function roughly corresponds to the rectangle rule. Modify the rule and write a test for the accuracy of:

   1. the trapezoidal rule;
   2. *the Simpson’s

   rule.* http://en.wikipedia.org/wiki/Simpson%27s_rule

   Exercise 4: Explain the recursive behavior of integration:

   1. In paddle game implemented by stream processing – *Lec10b.ml*, do we look at past velocity to determine current position, at past position to determine current velocity, both, or neither?
   2. What is the difference between *integral* and *integral_nice* in *Lec10c.ml*, what happens when we replace the former with the latter in the *pbal* function? How about after rewriting *pbal* into pure style as in the following exercise?

   Exercise 5: Reimplement the Froc based paddle ball example in a pure style: rewrite the pbal function to not use notify_e.

   Exercise 6: * Our implementation of flows is a bit heavy. One alternative approach is to use continuations, as in Scala.React. OCaml has a continuations library Delimcc; for how it can cooperate with Froc, seehttp://ambassadortothecomputers.blogspot.com/2010/08/mixing-monadic-and-direct-style-code.html

   Exercise 7: Implement parallel for flows, retaining coarse-grained implementation and using the event queue from Froc somehow (instead of introducing a new job queue).

   Exercise 8: Add quitting, e.g. via a 'q' key press, to the painter example. Use the is_cancelled function.

   Exercise 9: Our calculator example is not finished. Implement entering decimal fractions: add handling of the dots event.

   Exercise 10: The Flow module has reader monad functions that have not been discussed on slides:let local f m = fun emit -> m (fun x -> emit (f x))let localopt f m = fun emit -> m (fun x -> match f x with None -> () | Some y -> emit y)val local : (’a -> ’b) -> (’a, ’c) flow -> (’b, ’c) flowval localopt : (’a -> ’b option) -> (’a, ’c) flow -> (’b, ’c) flow

   Implement an example that uses this compositionality-increasing capability.

   The Expression Problem

   The Expression Problem

   Code organization, extensibility and reuse

   • Ralf Lämmel lectures on MSDN’s Channel 9:The Expression Problem, Haskell’s Type Classes

   • The old book Developing Applications with Objective Caml:Comparison of Modules and Objects, Extending Components

   • The new book Real World OCaml: Chapter 11: Objects, Chapter 12: Classes

   • Jacques Garrigue’s Code reuse through polymorphic variants,and Recursive Modules for Programming with Keiko Nakata

   • Extensible variant types

   • Graham Hutton’s and Erik Meijer’s Monadic Parser CombinatorsThe Expression Problem: Definition

   • The Expression Problem: design an implementation for expressions, where:

     • new variants of expressions can be added (datatype extensibility),
     • new operations on the expressions can be added (functional extensibility).

   • By extensibility we mean three conditions:

     • code-level modularization: the new datatype variants, and new operations, are in separate files,
     • separate compilation: the files can be compiled and distributed separately,
     • static type safety: we do not lose the type checking help and guarantees.

   • The name comes from an example: extend a language of expressions with new constructs:

     • lambda calculus: variables Var, \lambda-abstractions Abs, function applications App;
     • arithmetics: variables Var, constants Num, addition Add, multiplication Mult; …

     and new oparations:

     • evaluation eval;
     • pretty-printing to strings string_of;
     • free variables free_vars; …Functional Programming Non-solution: ordinary Algebraic Datatypes

   • Pattern matching makes functional extensibility easy in functional programming.

   • Ensuring datatype extensibility is complicated when using standard variant types.

   • For brevity, we will place examples in a single file, but the component type and function definitions are not mutually recursive so can be put in separate modules.

   • Non-solution penalty points:

     • Functions implemented for a broader language (e.g. lexpr_t) cannot be used with a value from a narrower langugage (e.g. expr_t).
     • Significant memory (and some time) overhead due to so called tagging: work of the wrap and unwrap functions, adding tags e.g. Lambda and Expr.
     • Some code bloat due to tagging. For example, deep pattern matching needs to be manually unrolled and interspersed with calls to unwrap.

     Verdict: non-solution, but better than extensible variant types-based approach (next) and direct OOP approach (later).

   type0.5emvar0.5em=0.5emstringVariables constitute a sub-language of its own.We treat this sub-language slightly differently – no need for a dedicated variant.let0.5emevalvar0.5emwrap0.5emsub0.5em(s0.5em:0.5emvar)0.5em=0.5em0.5emtry0.5emList.assoc0.5ems0.5emsub0.5emwith0.5emNotfound0.5em->0.5emwrap0.5emstype0.5em’a0.5emlambda0.5em=Here we define the sub-language of \lambda-expressions.0.5em0.5emVarL0.5emof0.5emvar0.5em|0.5emAbs0.5emof0.5emstring0.5em0.5em’a0.5em|0.5emApp0.5emof0.5em’a0.5em0.5em’aDuring evaluation, we need to freshen variables to avoid capturelet0.5emgensym0.5em=0.5emlet0.5emn0.5em=0.5emref0.5em00.5emin0.5emfun0.5em()0.5em->0.5emincr0.5emn;0.5em”“0.5emˆ0.5emstringofint0.5em!n(mistaking distinct variables with the same name).let0.5emevallambda0.5emevalrec0.5emwrap0.5emunwrap0.5emsubst0.5eme0.5em=0.5em0.5emmatch0.5emunwrap0.5eme0.5emwithAlternatively, unwrapping could use an exception,0.5em0.5em|0.5emSome0.5em(VarL0.5emv)0.5em->0.5emevalvar0.5em(fun0.5emv0.5em->0.5emwrap0.5em(VarL0.5emv))0.5emsubst0.5emv0.5em0.5em|0.5emSome0.5em(App0.5em(l1,0.5eml2))0.5em->but we use the option type as it is safer0.5em0.5em0.5em0.5emlet0.5eml1’0.5em=0.5emevalrec0.5emsubst0.5eml1and more flexible in this context.0.5em0.5em0.5em0.5emand0.5eml2’0.5em=0.5emevalrec0.5emsubst0.5eml20.5eminRecursive processing function returns expression0.5em0.5em0.5em0.5em(match0.5emunwrap0.5eml1’0.5emwithof the completed language, we need0.5em0.5em0.5em0.5em|0.5emSome0.5em(Abs0.5em(s,0.5embody))0.5em->to unwrap it into the current sub-language.0.5em0.5em0.5em0.5em0.5em0.5emevalrec0.5em[s,0.5eml2’]0.5embodyThe recursive call is already wrapped.0.5em0.5em0.5em0.5em|0.5em0.5em _ ->0.5emwrap0.5em(App0.5em(l1’,0.5eml2’)))Wrap into the completed language.0.5em0.5em0.5emSome0.5em(Abs0.5em(s,0.5eml1))0.5em->0.5em0.5em0.5em0.5emlet0.5ems’0.5em=0.5emgensym0.5em()0.5eminRename variable to avoid capture (\alpha-equivalence).0.5em0.5em0.5em0.5emwrap0.5em(Abs0.5em(s’,0.5emevalrec0.5em((s,0.5emwrap0.5em(VarL0.5ems’))::subst)0.5eml1))0.5em0.5em0.5emNone0.5em->0.5emeFalling-through when not in the current sub-language.type0.5emlambdat0.5em=0.5emLambdat0.5emof0.5emlambdat0.5emlambdaDefining \lambda-expressionsas the completed language,let0.5emrec0.5emeval10.5emsubst0.5em=and the corresponding eval function.0.5em0.5emevallambda0.5emeval10.5em0.5em0.5em0.5em(fun0.5eme0.5em->0.5emLambdat0.5eme)0.5em(fun0.5em(Lambdat0.5eme)0.5em->0.5emSome0.5eme)0.5emsubsttype0.5em’a0.5emexpr0.5em=The sub-language of arithmetic expressions.0.5em0.5emVarE0.5emof0.5emvar0.5em0.5emNum0.5emof0.5emint0.5em0.5emAdd0.5emof0.5em’a0.5em0.5em’a0.5em0.5emMult0.5emof0.5em’a0.5em0.5em’alet0.5emevalexpr0.5emevalrec0.5emwrap0.5emunwrap0.5emsubst0.5eme0.5em=0.5em0.5emmatch0.5emunwrap0.5eme0.5emwith0.5em0.5em0.5emSome0.5em(Num0.5em)0.5em->0.5eme0.5em0.5em0.5emSome0.5em(VarE0.5emv)0.5em->0.5em0.5em0.5em0.5emevalvar0.5em(fun0.5emx0.5em->0.5emwrap0.5em(VarE0.5emx))0.5emsubst0.5emv0.5em0.5em0.5emSome0.5em(Add0.5em(m,0.5emn))0.5em->0.5em0.5em0.5em0.5emlet0.5emm’0.5em=0.5emevalrec0.5emsubst0.5emm0.5em0.5em0.5em0.5emand0.5emn’0.5em=0.5emevalrec0.5emsubst0.5emn0.5emin0.5em0.5em0.5em0.5em(match0.5emunwrap0.5emm’,0.5emunwrap0.5emn’0.5emwithUnwrapping to check if the subexpressions0.5em0.5em0.5em0.5em0.5emSome0.5em(Num0.5emm’),0.5emSome0.5em(Num0.5emn’)0.5em->got computed to values.0.5em0.5em0.5em0.5em0.5em0.5emwrap0.5em(Num0.5em(m’0.5em+0.5emn’))0.5em0.5em0.5em0.5em->0.5emwrap0.5em(Add0.5em(m’,0.5emn’)))Here m' and n' are wrapped.0.5em0.5em0.5emSome0.5em(Mult0.5em(m,0.5emn))0.5em->0.5em0.5em0.5em0.5emlet0.5emm’0.5em=0.5emevalrec0.5emsubst0.5emm0.5em0.5em0.5em0.5emand0.5emn’0.5em=0.5emevalrec0.5emsubst0.5emn0.5emin0.5em0.5em0.5em0.5em(match0.5emunwrap0.5emm’,0.5emunwrap0.5emn’0.5emwith0.5em0.5em0.5em0.5em0.5emSome0.5em(Num0.5emm’),0.5emSome0.5em(Num0.5emn’)0.5em->0.5em0.5em0.5em0.5em0.5em0.5emwrap0.5em(Num0.5em(m’0.5em*0.5emn’))0.5em0.5em0.5em0.5em->0.5emwrap0.5em(Mult0.5em(m’,0.5emn’)))0.5em0.5em0.5emNone0.5em->0.5emetype0.5emexprt0.5em=0.5emExprt0.5emof0.5emexprt0.5emexprDefining arithmetic expressionsas the completed language,let0.5emrec0.5emeval20.5emsubst0.5em=aka. ‘‘tying the recursive knot’‘.0.5em0.5emevalexpr0.5emeval20.5em0.5em0.5em0.5em(fun0.5eme0.5em->0.5emExprt0.5eme)0.5em(fun0.5em(Exprt0.5eme)0.5em->0.5emSome0.5eme)0.5emsubsttype0.5em’a0.5emlexpr0.5em=The language merging \lambda-expressions and arithmetic expressions,0.5em0.5emLambda0.5emof0.5em’a0.5emlambda0.5em0.5emExpr0.5emof0.5em’a0.5emexprcan also be used asa sub-language for further extensions.let0.5emevallexpr0.5emevalrec0.5emwrap0.5emunwrap0.5emsubst0.5eme0.5em=0.5em0.5emevallambda0.5emevalrec0.5em0.5em0.5em0.5em(fun0.5eme0.5em->0.5emwrap0.5em(Lambda0.5eme))0.5em0.5em0.5em0.5em(fun0.5eme0.5em->0.5em0.5em0.5em0.5em0.5em0.5emmatch0.5emunwrap0.5eme0.5emwith0.5em0.5em0.5em0.5em0.5em0.5em0.5emSome0.5em(Lambda0.5eme)0.5em->0.5emSome0.5eme0.5em0.5em0.5em0.5em0.5em0.5em->0.5emNone)0.5em0.5em0.5em0.5emsubst0.5em0.5em0.5em0.5em(evalexpr0.5emevalrecWe use the ‘‘fall-through’’ property of eval_expr``0.5em0.5em0.5em0.5em0.5em0.5em0.5em(fun0.5eme0.5em->0.5emwrap0.5em(Expr0.5eme))to combine the evaluators.0.5em0.5em0.5em0.5em0.5em0.5em0.5em(fun0.5eme0.5em->0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5emmatch0.5emunwrap0.5eme0.5emwith0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5emSome0.5em(Expr0.5eme)0.5em->0.5emSome0.5eme0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em->0.5emNone)0.5em0.5em0.5em0.5em0.5em0.5em0.5emsubst0.5eme)type0.5emlexprt0.5em=0.5emLExprt0.5emof0.5emlexprt0.5emlexprTying the recursive knot one last time.let0.5emrec0.5emeval30.5emsubst0.5em=0.5em0.5emevallexpr0.5emeval30.5em0.5em0.5em0.5em(fun0.5eme0.5em->0.5emLExprt0.5eme)0.5em0.5em0.5em0.5em(fun0.5em(LExprt0.5eme)0.5em->0.5emSome0.5eme)0.5emsubstLightweight FP non-solution: Extensible Variant Types

   • Exceptions have always formed an extensible variant type in OCaml, whose pattern matching is done using the try\ldotswith syntax. Since recently, new extensible variant types can be defined. This augments the normal function extensibility of FP with straightforward data extensibility.
   • Non-solution penalty points:
     • Giving up exhaustivity checking, which is an important aspect of static type safety.
     • More natural with “single inheritance” extension chains, although merging is possible, and demonstrated in our example.
     • Requires “tying the recursive knot” for functions.
     Verdict: pleasant-looking, but the worst approach because of possible bugginess. Unless bug-proneness is not a concern, then the best approach.

   type0.5emexpr0.5em=0.5em..This is how extensible variant types are defined.type0.5emvarname0.5em=0.5emstringtype0.5emexpr0.5em+=0.5emVar0.5emof0.5emstringWe add a variant case.let0.5emevalvar0.5emsub0.5em=0.5emfunction0.5em0.5em0.5emVar0.5ems0.5emas0.5emv0.5em->0.5em(try0.5emList.assoc0.5ems0.5emsub0.5emwith0.5emNotfound0.5em->0.5emv)0.5em0.5em0.5eme0.5em->0.5emelet0.5emgensym0.5em=0.5emlet0.5emn0.5em=0.5emref0.5em00.5emin0.5emfun0.5em()0.5em->0.5emincr0.5emn;0.5em”“0.5em0.5emstringofint0.5em!ntype0.5emexpr0.5em+=0.5emAbs0.5emof0.5emstring0.5em0.5emexpr0.5em0.5emApp0.5emof0.5emexpr0.5em0.5emexprThe sub-languagesare not differentiated by types, a shortcoming of this non-solution.let0.5emevallambda0.5emevalrec0.5emsubst0.5em=0.5emfunction0.5em0.5em0.5emVar0.5em0.5emas0.5emv0.5em->0.5emevalvar0.5emsubst0.5emv0.5em0.5em0.5emApp0.5em(l1,0.5eml2)0.5em->0.5em0.5em0.5em0.5emlet0.5eml2’0.5em=0.5emevalrec0.5emsubst0.5eml20.5emin0.5em0.5em0.5em0.5em(match0.5emevalrec0.5emsubst0.5eml10.5emwith0.5em0.5em0.5em0.5em0.5emAbs0.5em(s,0.5embody)0.5em->0.5em0.5em0.5em0.5em0.5em0.5emevalrec0.5em[s,0.5eml2’]0.5embody0.5em0.5em0.5em0.5em0.5eml1’0.5em->0.5emApp0.5em(l1’,0.5eml2’))0.5em0.5em0.5emAbs0.5em(s,0.5eml1)0.5em->0.5em0.5em0.5em0.5emlet0.5ems’0.5em=0.5emgensym0.5em()0.5emin0.5em0.5em0.5em0.5emAbs0.5em(s’,0.5emevalrec0.5em((s,0.5emVar0.5ems’)::subst)0.5eml1)0.5em0.5em0.5eme0.5em->0.5emelet0.5emfreevarslambda0.5emfreevarsrec0.5em=0.5emfunction0.5em0.5em0.5emVar0.5emv0.5em->0.5em[v]0.5em0.5em0.5emApp0.5em(l1,0.5eml2)0.5em->0.5emfreevarsrec0.5eml10.5em@0.5emfreevarsrec0.5eml20.5em0.5em0.5emAbs0.5em(s,0.5eml1)0.5em->0.5em0.5em0.5em0.5emList.filter0.5em(fun0.5emv0.5em->0.5emv0.5em<>0.5ems)0.5em(freevarsrec0.5eml1)0.5em0.5em->0.5em[]let0.5emrec0.5emeval10.5emsubst0.5eme0.5em=0.5emevallambda0.5emeval10.5emsubst0.5emelet0.5emrec0.5emfreevars10.5eme0.5em=0.5emfreevarslambda0.5emfreevars10.5emelet0.5emtest10.5em=0.5emApp0.5em(Abs0.5em(”x”,0.5emVar0.5em”x”),0.5emVar0.5em”y”)let0.5emetest0.5em=0.5emeval10.5em[]0.5emtest1let0.5emfvtest0.5em=0.5emfreevars10.5emtest1type0.5emexpr0.5em+=0.5emNum0.5emof0.5emint0.5em0.5emAdd0.5emof0.5emexpr0.5em0.5emexpr0.5em0.5emMult0.5emof0.5emexpr0.5em0.5emexprlet0.5emmapexpr0.5emf0.5em=0.5emfunction0.5em0.5em0.5emAdd0.5em(e1,0.5eme2)0.5em->0.5emAdd0.5em(f0.5eme1,0.5emf0.5eme2)0.5em0.5em0.5emMult0.5em(e1,0.5eme2)0.5em->0.5emMult0.5em(f0.5eme1,0.5emf0.5eme2)0.5em0.5em0.5eme0.5em->0.5emelet0.5emevalexpr0.5emevalrec0.5emsubst0.5eme0.5em=0.5em0.5emmatch0.5emmapexpr0.5em(evalrec0.5emsubst)0.5eme0.5emwith0.5em0.5em0.5emAdd0.5em(Num0.5emm,0.5emNum0.5emn)0.5em->0.5emNum0.5em(m0.5em+0.5emn)0.5em0.5em0.5emMult0.5em(Num0.5emm,0.5emNum0.5emn)0.5em->0.5emNum0.5em(m0.5em*0.5emn)0.5em0.5em0.5em(Num0.5em0.5em0.5emAdd0.5em0.5em0.5emMult0.5em)0.5emas0.5eme0.5em->0.5eme0.5em0.5em0.5eme0.5em->0.5emelet0.5emfreevarsexpr0.5emfreevarsrec0.5em=0.5emfunction0.5em0.5em0.5emNum0.5em0.5em->0.5em[]0.5em0.5em0.5emAdd0.5em(e1,0.5eme2)0.5em0.5emMult0.5em(e1,0.5eme2)0.5em->0.5emfreevarsrec0.5eme10.5em@0.5emfreevarsrec0.5eme20.5em0.5em->0.5em[]let0.5emrec0.5emeval20.5emsubst0.5eme0.5em=0.5emevalexpr0.5emeval20.5emsubst0.5emelet0.5emrec0.5emfreevars20.5eme0.5em=0.5emfreevarsexpr0.5emfreevars20.5emelet0.5emtest20.5em=0.5emAdd0.5em(Mult0.5em(Num0.5em3,0.5emVar0.5em”x”),0.5emNum0.5em1)let0.5emetest20.5em=0.5emeval20.5em[]0.5emtest2let0.5emfvtest20.5em=0.5emfreevars20.5emtest2let0.5emevallexpr0.5emevalrec0.5emsubst0.5eme0.5em=0.5em0.5emevalexpr0.5emevalrec0.5emsubst0.5em(evallambda0.5emevalrec0.5emsubst0.5eme)let0.5emfreevarslexpr0.5emfreevarsrec0.5eme0.5em=0.5em0.5emfreevarslambda0.5emfreevarsrec0.5eme0.5em@0.5emfreevarsexpr0.5emfreevarsrec0.5emelet0.5emrec0.5emeval30.5emsubst0.5eme0.5em=0.5emevallexpr0.5emeval30.5emsubst0.5emelet0.5emrec0.5emfreevars30.5eme0.5em=0.5emfreevarslexpr0.5emfreevars30.5emelet0.5emtest30.5em=0.5em0.5emApp0.5em(Abs0.5em(“x”,0.5emAdd0.5em(Mult0.5em(Num0.5em3,0.5emVar0.5em”x”),0.5emNum0.5em1)),0.5em0.5em0.5em0.5em0.5em0.5em0.5emNum0.5em2)let0.5emetest30.5em=0.5emeval30.5em[]0.5emtest3let0.5emfvtest30.5em=0.5emfreevars30.5emtest3Object Oriented Programming: Subtyping

   • OCaml’s objects are values, somewhat similar to records.
   • Viewed from the outside, an OCaml object has only methods, identifying the code with which to respond to messages, i.e. method invocations.
   • All methods are late-bound, the object determines what code is run (i.e. virtual in C++ parlance).
   • Subtyping determines if an object can be used in some context. OCaml has structural subtyping: the content of the types concerned decides if an object can be used.
   • Parametric polymorphism can be used to infer if an object has the required methods.

   let0.5emf0.5emx0.5em=0.5emx#mMethod invocation: object#method.val0.5emf0.5em:0.5em<0.5emm0.5em:0.5em’a;0.5em..0.5em>0.5em->0.5em’aType poymorphic in two ways: 'a is the method type,.. means that objects with more methods will be accepted.

   • Methods are computed when they are invoked, even if they do not take arguments.

   • We define objects inside object…end (compare: records {…}) using keywords method for methods, val for constant fields and val mutable for mutable fields. Constructor arguments can often be used instead of constant fields:

     let0.5emsquare0.5emw0.5em=0.5emobject0.5em0.5emmethod0.5emarea0.5em=0.5emfloatofint0.5em(w0.5em*0.5emw)0.5emmethod0.5emwidth0.5em=0.5emw0.5emend

   • Subtyping often needs to be explicit: we write (object :> supertype) or in more complex cases (object : type :> supertype).

     • Technically speaking, subtyping in OCaml always is explicit, and open types, containing .., use row polymorphism rather than subtyping.

   let0.5ema0.5em=0.5emobject0.5emmethod0.5emm0.5em=0.5em70.5em0.5emmethod0.5emx0.5em=0.5em”a”0.5emendToy example: object typeslet0.5emb0.5em=0.5emobject0.5emmethod0.5emm0.5em=0.5em420.5emmethod0.5emy0.5em=0.5em”b”0.5emendshare some but not all methods.let0.5eml0.5em=0.5em[a;0.5emb]The exact types of the objects do not agree.Error:0.5emThis0.5emexpression0.5emhas0.5emtype0.5em<0.5emm0.5em:0.5emint;0.5emy0.5em:0.5emstring0.5em>0.5em0.5em0.5em0.5em0.5em0.5em0.5embut0.5eman0.5emexpression0.5emwas0.5emexpected0.5emof0.5emtype0.5em<0.5emm0.5em:0.5emint;0.5emx0.5em:0.5emstring0.5em>0.5em0.5em0.5em0.5em0.5em0.5em0.5emThe0.5emsecond0.5emobject0.5emtype0.5emhas0.5emno0.5emmethod0.5emylet0.5eml0.5em=0.5em[(a0.5em:>0.5em<m0.5em:0.5em’a>);0.5em(b0.5em:>0.5em<m0.5em:0.5em’a>)]But the types share a supertype.val0.5eml0.5em:0.5em<0.5emm0.5em:0.5emint0.5em>0.5emlist

   • Variance determines how type parameters behave wrt. subtyping:

     • Invariant parameters cannot be subtyped:

       let0.5emf0.5emx0.5em=0.5em(x0.5em:0.5em<m0.5em:0.5emint;0.5emn0.5em:0.5emfloat>0.5emarray0.5em:>0.5em<m0.5em:0.5emint>0.5emarray)Error:0.5emType0.5em<0.5emm0.5em:0.5emint;0.5emn0.5em:0.5emfloat0.5em>0.5emarray0.5emis0.5emnot0.5ema0.5emsubtype0.5emof0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em<0.5emm0.5em:0.5emint0.5em>0.5emarray0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5emThe0.5emsecond0.5emobject0.5emtype0.5emhas0.5emno0.5emmethod0.5emn

     • Covariant parameters are subtyped in the same direction as the type:

       let0.5emf0.5emx0.5em=0.5em(x0.5em:0.5em<m0.5em:0.5emint;0.5emn0.5em:0.5emfloat>0.5emlist0.5em:>0.5em<m0.5em:0.5emint>0.5emlist)val0.5emf0.5em:0.5em<0.5emm0.5em:0.5emint;0.5emn0.5em:0.5emfloat0.5em>0.5emlist0.5em->0.5em<0.5emm0.5em:0.5emint0.5em>0.5emlist

     • Contravariant parameters are subtyped in the opposite direction:

       let0.5emf0.5emx0.5em=0.5em(x0.5em:0.5em<m0.5em:0.5emint;0.5emn0.5em:0.5emfloat>0.5em->0.5emfloat0.5em:>0.5em<m0.5em:0.5emint>0.5em->0.5emfloat)Error:0.5emType0.5em<0.5emm0.5em:0.5emint;0.5emn0.5em:0.5emfloat0.5em>0.5em->0.5emfloat0.5emis0.5emnot0.5ema0.5emsubtype0.5emof0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em<0.5emm0.5em:0.5emint0.5em>0.5em->0.5emfloat0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5emType0.5em<0.5emm0.5em:0.5emint0.5em>0.5emis0.5emnot0.5ema0.5emsubtype0.5emof0.5em<0.5emm0.5em:0.5emint;0.5emn0.5em:0.5emfloat0.5em>0.5emlet0.5emf0.5emx0.5em=0.5em(x0.5em:0.5em<m0.5em:0.5emint>0.5em->0.5emfloat0.5em:>0.5em<m0.5em:0.5emint;0.5emn0.5em:0.5emfloat>0.5em->0.5emfloat)val0.5emf0.5em:0.5em(<0.5emm0.5em:0.5emint0.5em>0.5em->0.5emfloat)0.5em->0.5em<0.5emm0.5em:0.5emint;0.5emn0.5em:0.5emfloat0.5em>0.5em->0.5emfloatObject Oriented Programming: Inheritance

   • The system of object classes in OCaml is similar to the module system.
     • Object classes are not types. Classes are a way to build object constructors – functions that return objects.
     • Classes have their types (compare: modules and signatures).
   • In OCaml parlance:
     • late binding is not called anything – all methods are late-bound (in C++ called virtual)
     • a method or field declared to be defined in sub-classes is virtual (in C++ called abstract); classes that use virtual methods or fields are also called virtual
     • a method that is only visible in sub-classes is private (in C++ called protected)
     • a method not visible outside the class is not called anything (in C++ called private) – provide the type for the class, and omit the method in the class type (compare: module signatures and .mli files)
   • OCaml allows multiple inheritance, which can be used to implement mixins as virtual / abstract classes.
   • Inheritance works somewhat similarly to textual inclusion.
   • See the excellent examples in https://realworldocaml.org/v1/en/html/classes.html
   • You can perform ocamlc -i Objects.ml etc. to see inferred object and class types.

   OOP Non-solution: direct approach

   • It turns out that although object oriented programming was designed with data extensibility in mind, it is a bad fit for recursive types, like in the expression problem. Below is my attempt at solving our problem using classes – can you do better?
   • Non-solution penalty points:
     • Functions implemented for a broader language (e.g. corresponding to lexpr_t on other slides) cannot handle values from a narrower one (e.g.  corresponding to expr_t).
     • Writing a new function requires extending the language.
     • No deep pattern matching.
     Verdict: non-solution, better only than the extensible variant types-based approach.

   type0.5emvarname0.5em=0.5emstringlet0.5emgensym0.5em=0.5emlet0.5emn0.5em=0.5emref0.5em00.5emin0.5emfun0.5em()0.5em->0.5emincr0.5emn;0.5em”“0.5em0.5emstringofint0.5em!nclass0.5emvirtual0.5em[’lang]0.5emevaluable0.5em=The abstract class for objects supporting the eval method.object0.5emFor \lambda-calculus, we need helper functions:0.5em0.5emmethod0.5emvirtual0.5emeval0.5em:0.5em(varname0.5em0.5em’lang)0.5emlist0.5em->0.5em’lang0.5em0.5emmethod0.5emvirtual0.5emrename0.5em:0.5emvarname0.5em->0.5emvarname0.5em->0.5em'langrenaming of free variables,0.5em0.5emmethod0.5emapply0.5em(arg0.5em:0.5em’lang)\beta-reduction if possible (fallback otherwise).0.5em0.5em0.5em0.5em(fallback0.5em:0.5emunit0.5em->0.5em’lang)0.5em(subst0.5em:0.5em(varname0.5em0.5em’lang)0.5emlist)0.5em=0.5em0.5em0.5em0.5emfallback0.5em()endclass0.5em[’lang]0.5emvar0.5em(v0.5em:0.5emvarname)0.5em=object0.5em(self)We name the current object self.0.5em0.5eminherit0.5em[’lang]0.5emevaluable0.5em0.5emval0.5emv0.5em=0.5emv0.5em0.5emmethod0.5emeval0.5emsubst0.5em=0.5em0.5em0.5em0.5emtry0.5emList.assoc0.5emv0.5emsubst0.5emwith0.5emNotfound0.5em->0.5emself0.5em0.5emmethod0.5emrename0.5emv10.5emv20.5em=Renaming a variable:0.5em0.5em0.5em0.5emif0.5emv0.5em=0.5emv10.5emthen0.5em{<0.5emv0.5em=0.5emv20.5em>}0.5emelse0.5emselfwe clone the current object putting the new name.endclass0.5em[’lang]0.5emabs0.5em(v0.5em:0.5emvarname)0.5em(body0.5em:0.5em’lang)0.5em=object0.5em(self)0.5em0.5eminherit0.5em[’lang]0.5emevaluable0.5em0.5emval0.5emv0.5em=0.5emv0.5em0.5emval0.5embody0.5em=0.5embody0.5em0.5emmethod0.5emeval0.5emsubst0.5em=We do \alpha-conversion prior to evaluation.0.5em0.5em0.5em0.5emlet0.5emv’0.5em=0.5emgensym0.5em()0.5eminAlternatively, we could evaluate with0.5em0.5em0.5em0.5em{<0.5emv0.5em=0.5emv’;0.5embody0.5em=0.5em(body#rename0.5emv0.5emv’)#eval0.5emsubst0.5em>}substitution of v0.5em0.5emmethod0.5emrename0.5emv10.5emv20.5em=by v_inst v' : 'lang similar to num_inst below.0.5em0.5em0.5em0.5emif0.5emv0.5em=0.5emv10.5emthen0.5emselfRenaming the free variable v1, so no work if v=v1.0.5em0.5em0.5em0.5emelse0.5em{<0.5embody0.5em=0.5embody#rename0.5emv10.5emv20.5em>}0.5em0.5emmethod0.5emapply0.5emargsubst0.5em=0.5em0.5em0.5em0.5embody#eval0.5em((v,0.5emarg)::subst)endclass0.5em[’lang]0.5emapp0.5em(f0.5em:0.5em’lang)0.5em(arg0.5em:0.5em’lang)0.5em=object0.5em(self)0.5em0.5eminherit0.5em[’lang]0.5emevaluable0.5em0.5emval0.5emf0.5em=0.5emf0.5em0.5emval0.5emarg0.5em=0.5emarg0.5em0.5emmethod0.5emeval0.5emsubst0.5em=We use apply to differentiate between f = abs0.5em0.5em0.5em0.5emlet0.5emarg’0.5em=0.5emarg#eval0.5emsubst0.5emin (\beta-redexes) and f ≠ abs.0.5em0.5em0.5em0.5emf#apply0.5emarg’0.5em(fun0.5em()0.5em->0.5em{<0.5emf0.5em=0.5emf#eval0.5emsubst;0.5emarg0.5em=0.5emarg’0.5em>})0.5emsubst0.5em0.5emmethod0.5emrename0.5emv10.5emv20.5em=Cloning the object ensures that it will be a subtype of 'lang0.5em0.5em0.5em0.5em{<0.5emf0.5em=0.5emf#rename0.5emv10.5emv2;0.5emarg0.5em=0.5emarg#rename0.5emv10.5emv20.5em>}rather than just 'lang app.endtype0.5emevaluablet0.5em=0.5emevaluablet0.5emevaluableThese definitions only add nice-looking types.let0.5emnewvar10.5emv0.5em:0.5emevaluablet0.5em=0.5emnew0.5emvar0.5emvlet0.5emnewabs10.5emv0.5em(body0.5em:0.5emevaluablet)0.5em:0.5emevaluablet0.5em=0.5emnew0.5emabs0.5emv0.5embodyclass0.5emvirtual0.5emcomputemixin0.5em=0.5emobjectFor evaluating arithmetic expressions we need0.5em0.5emmethod0.5emcompute0.5em:0.5emint0.5emoption0.5em=0.5emNone0.5em0.5ema heper method compute.endclass0.5em[’lang]0.5emvarc0.5emv0.5em=0.5emobjectTo use \lambda-expressions together with arithmetic expressions0.5em0.5eminherit0.5em[’lang]0.5emvar0.5emvwe need to upgrade them with the helper method.0.5em0.5eminherit0.5emcomputemixinendclass0.5em[’lang]0.5emabsc0.5emv0.5embody0.5em=0.5emobject0.5em0.5eminherit0.5em[’lang]0.5emabs0.5emv0.5embody0.5em0.5eminherit0.5emcomputemixinendclass0.5em[’lang]0.5emappc0.5emf0.5emarg0.5em=0.5emobject0.5em0.5eminherit0.5em[’lang]0.5emapp0.5emf0.5emarg0.5em0.5eminherit0.5emcomputemixinendclass0.5em[’lang]0.5emnum0.5em(i0.5em:0.5emint)0.5em=A numerical constant.object0.5em(self)0.5em0.5eminherit0.5em[’lang]0.5emevaluable0.5em0.5emval0.5emi0.5em=0.5emi0.5em0.5emmethod0.5emeval0.5emsubst0.5em=0.5emself0.5em0.5emmethod0.5emrename0.5em=0.5emself0.5em0.5emmethod0.5emcompute0.5em=0.5emSome0.5emiendclass0.5emvirtual0.5em[’lang]0.5emoperationAbstract class for evaluating arithmetic operations.0.5em0.5em0.5em0.5em(numinst0.5em:0.5emint0.5em->0.5em’lang)0.5em(n10.5em:0.5em’lang)0.5em(n20.5em:0.5em’lang)0.5em=object0.5em(self)0.5em0.5eminherit0.5em[’lang]0.5emevaluable0.5em0.5emval0.5emn10.5em=0.5emn10.5em0.5emval0.5emn20.5em=0.5emn20.5em0.5emmethod0.5emeval0.5emsubst0.5em=0.5em0.5em0.5em0.5emlet0.5emself’0.5em=0.5em{<0.5emn10.5em=0.5emn1#eval0.5emsubst;0.5emn20.5em=0.5emn2#eval0.5emsubst0.5em>}0.5emin0.5em0.5em0.5em0.5emmatch0.5emself’#compute0.5emwith0.5em0.5em0.5em0.5em0.5emSome0.5emi0.5em->0.5emnuminst0.5emiWe need to inject the integer as a constant that is0.5em0.5em0.5em0.5em->0.5emself'a subtype of 'lang.0.5em0.5emmethod0.5emrename0.5emv10.5emv20.5em=0.5em{<0.5emn10.5em=0.5emn1#rename0.5emv10.5emv2;0.5emn20.5em=0.5emn2#rename0.5emv10.5emv20.5em>}endclass0.5em[’lang]0.5emadd0.5emnuminst0.5emn10.5emn20.5em=object0.5em(self)0.5em0.5eminherit0.5em[’lang]0.5emoperation0.5emnuminst0.5emn10.5emn20.5em0.5emmethod0.5emcompute0.5em=If compute is called by eval, as intended,0.5em0.5em0.5em0.5emmatch0.5emn1#compute,0.5emn2#compute0.5emwiththen n1 and n2 are already computed.0.5em0.5em0.5em0.5em0.5emSome0.5emi1,0.5emSome0.5emi20.5em->0.5emSome0.5em(i10.5em+0.5emi2)0.5em0.5em0.5em0.5em->0.5emNoneendclass0.5em[’lang]0.5emmult0.5emnuminst0.5emn10.5emn20.5em=object0.5em(self)0.5em0.5eminherit0.5em[’lang]0.5emoperation0.5emnuminst0.5emn10.5emn20.5em0.5emmethod0.5emcompute0.5em=0.5em0.5em0.5em0.5emmatch0.5emn1#compute,0.5emn2#compute0.5emwith0.5em0.5em0.5em0.5em0.5emSome0.5emi1,0.5emSome0.5emi20.5em->0.5emSome0.5em(i10.5em*0.5emi2)0.5em0.5em0.5em0.5em->0.5emNoneendclass0.5emvirtual0.5em[’lang]0.5emcomputable0.5em=This class is defined merely to provide an object type,objectwe could also define this object type ‘‘by hand’’.0.5em0.5eminherit0.5em[’lang]0.5emevaluable0.5em0.5eminherit0.5emcomputemixinendtype0.5emcomputablet0.5em=0.5emcomputablet0.5emcomputableNice types for all the constructors.let0.5emnewvar20.5emv0.5em:0.5emcomputablet0.5em=0.5emnew0.5emvarc0.5emvlet0.5emnewabs20.5emv0.5em(body0.5em:0.5emcomputablet)0.5em:0.5emcomputablet0.5em=0.5emnew0.5emabsc0.5emv0.5embodylet0.5emnewapp20.5emv0.5em(body0.5em:0.5emcomputablet)0.5em:0.5emcomputablet0.5em=0.5emnew0.5emappc0.5emv0.5embodylet0.5emnewnum20.5emi0.5em:0.5emcomputablet0.5em=0.5emnew0.5emnum0.5emilet0.5emnewadd20.5em(n10.5em:0.5emcomputablet)0.5em(n20.5em:0.5emcomputablet)0.5em:0.5emcomputablet0.5em=0.5em0.5emnew0.5emadd0.5emnewnum20.5emn10.5emn2let0.5emnewmult20.5em(n10.5em:0.5emcomputablet)0.5em(n20.5em:0.5emcomputablet)0.5em:0.5emcomputablet0.5em=0.5em0.5emnew0.5emmult0.5emnewnum20.5emn10.5emn2OOP: The Visitor Pattern

   • The Visitor Pattern is an object-oriented programming pattern for turning objects into variants with shallow pattern-matching (i.e. dispatch based on which variant a value is). It replaces data extensibility by operation extensibility.
   • I needed to use imperative features (mutable fields), can you do better?
   • Penalty points:
     • Heavy code bloat.
     • Side-effects appear to be required.
     • No deep pattern matching.
     Verdict: poor solution, better than approaches we considered so far, and worse than approaches we consider next.

   type0.5em’visitor0.5emvisitable0.5em=0.5em<0.5emaccept0.5em:0.5em’visitor0.5em->0.5emunit0.5em>The variants need be visitable.We store the computation as side effect because of the difficultytype0.5emvarname0.5em=0.5emstringto keep the visitor polymorphic but have the result typedepend on the visitor.class0.5em[’visitor]0.5emvar0.5em(v0.5em:0.5emvarname)0.5em=The 'visitor will determine the (sub)languageobject0.5em(self)to which a given var variant belongs.0.5em0.5emmethod0.5emv0.5em=0.5emv0.5em0.5emmethod0.5emaccept0.5em:0.5em’visitor0.5em->0.5emunit0.5em=The visitor pattern inverts the way0.5em0.5em0.5em0.5emfun0.5emvisitor0.5em->0.5emvisitor#visitVar0.5emselfpattern matching proceeds: the variantendselects the pattern matching branch.let0.5emnewvar0.5emv0.5em=0.5em(new0.5emvar0.5emv0.5em:>0.5em’a0.5emvisitable)Visitors need to see the stored data,but distinct constructors need to belong to the same type.class0.5em[’visitor]0.5emabs0.5em(v0.5em:0.5emvarname)0.5em(body0.5em:0.5em’visitor0.5emvisitable)0.5em=object0.5em(self)0.5em0.5emmethod0.5emv0.5em=0.5emv0.5em0.5emmethod0.5embody0.5em=0.5embody0.5em0.5emmethod0.5emaccept0.5em:0.5em’visitor0.5em->0.5emunit0.5em=0.5em0.5em0.5em0.5emfun0.5emvisitor0.5em->0.5emvisitor#visitAbs0.5emselfendlet0.5emnewabs0.5emv0.5embody0.5em=0.5em(new0.5emabs0.5emv0.5embody0.5em:>0.5em’a0.5emvisitable)class0.5em[’visitor]0.5emapp0.5em(f0.5em:0.5em’visitor0.5emvisitable)0.5em(arg0.5em:0.5em’visitor0.5emvisitable)0.5em=object0.5em(self)0.5em0.5emmethod0.5emf0.5em=0.5emf0.5em0.5emmethod0.5emarg0.5em=0.5emarg0.5em0.5emmethod0.5emaccept0.5em:0.5em’visitor0.5em->0.5emunit0.5em=0.5em0.5em0.5em0.5emfun0.5emvisitor0.5em->0.5emvisitor#visitApp0.5emselfendlet0.5emnewapp0.5emf0.5emarg0.5em=0.5em(new0.5emapp0.5emf0.5emarg0.5em:>0.5em’a0.5emvisitable)class0.5emvirtual0.5em[’visitor]0.5emlambdavisit0.5em=This abstract class has two uses:objectit defines the visitors for the sub-langauge of \lambda-expressions,0.5em0.5emmethod0.5emvirtual0.5emvisitVar0.5em:0.5em’visitor0.5emvar0.5em->0.5emunitand it will provide an early check0.5em0.5emmethod0.5emvirtual0.5emvisitAbs0.5em:0.5em’visitor0.5emabs0.5em->0.5emunitthat the visitor classes0.5em0.5emmethod0.5emvirtual0.5emvisitApp0.5em:0.5em’visitor0.5emapp0.5em->0.5emunitimplement all the methods.endlet0.5emgensym0.5em=0.5emlet0.5emn0.5em=0.5emref0.5em00.5emin0.5emfun0.5em()0.5em->0.5emincr0.5emn;0.5em”“0.5em0.5emstringofint0.5em!nclass0.5em[’visitor]0.5emevallambda0.5em0.5em(subst0.5em:0.5em(varname0.5em0.5em’visitor0.5emvisitable)0.5emlist)0.5em0.5em(result0.5em:0.5em’visitor0.5emvisitable0.5emref)0.5em=An output argument, but also used internallyobject0.5em(self)to store intermediate results.0.5em0.5eminherit0.5em[’visitor]0.5emlambdavisit0.5em0.5emval0.5emmutable0.5emsubst0.5em=0.5emsubstWe avoid threading the argument through the visit methods.0.5em0.5emval0.5emmutable0.5embetaredex0.5em:0.5em(varname0.5em0.5em’visitor0.5emvisitable)0.5emoption0.5em=0.5emNoneWe work around0.5em0.5emmethod0.5emvisitVar0.5emvar0.5em=the need to differentiate between abs and non-abs values0.5em0.5em0.5em0.5embetaredex0.5em<-0.5emNone;of app#f inside visitApp.0.5em0.5em0.5em0.5emtry0.5emresult0.5em:=0.5emList.assoc0.5emvar#v0.5emsubst0.5em0.5em0.5em0.5emwith0.5emNotfound0.5em->0.5emresult0.5em:=0.5em(var0.5em:>0.5em’visitor0.5emvisitable)0.5em0.5emmethod0.5emvisitAbs0.5emabs0.5em=0.5em0.5em0.5em0.5emlet0.5emv’0.5em=0.5emgensym0.5em()0.5emin0.5em0.5em0.5em0.5emlet0.5emorigsubst0.5em=0.5emsubst0.5emin0.5em0.5em0.5em0.5emsubst0.5em<-0.5em(abs#v,0.5emnew_var0.5emv’)::subst;‘‘Pass’’ the updated substitution0.5em0.5em0.5em0.5em(abs#body)#accept0.5emself;to the recursive call0.5em0.5em0.5em0.5emlet0.5embody’0.5em=0.5em!result0.5eminand collect the result of the recursive call.0.5em0.5em0.5em0.5emsubst0.5em<-0.5emorigsubst;0.5em0.5em0.5em0.5embetaredex0.5em<-0.5emSome0.5em(v’,0.5embody’);Indicate that an abs has just been visited.0.5em0.5em0.5em0.5emresult0.5em:=0.5emnewabs0.5emv’0.5embody’0.5em0.5emmethod0.5emvisitApp0.5emapp0.5em=0.5em0.5em0.5em0.5emapp#arg#accept0.5emself;0.5em0.5em0.5em0.5emlet0.5emarg’0.5em=0.5em!result0.5emin0.5em0.5em0.5em0.5emapp#f#accept0.5emself;0.5em0.5em0.5em0.5emlet0.5emf’0.5em=0.5em!result0.5emin0.5em0.5em0.5em0.5emmatch0.5embetaredex0.5emwithPattern-match on app#f.0.5em0.5em0.5em0.5em0.5emSome0.5em(v’,0.5embody’)0.5em->0.5em0.5em0.5em0.5em0.5em0.5embetaredex0.5em<-0.5emNone;0.5em0.5em0.5em0.5em0.5em0.5emlet0.5emorigsubst0.5em=0.5emsubst0.5emin0.5em0.5em0.5em0.5em0.5em0.5emsubst0.5em<-0.5em(v’,0.5emarg’)::subst;0.5em0.5em0.5em0.5em0.5em0.5embody’#accept0.5emself;0.5em0.5em0.5em0.5em0.5em0.5emsubst0.5em<-0.5emorigsubst0.5em0.5em0.5em0.5em0.5emNone0.5em->0.5emresult0.5em:=0.5emnewapp0.5emf’0.5emarg’endclass0.5em[’visitor]0.5emfreevarslambda0.5em(result0.5em:0.5emvarname0.5emlist0.5emref)0.5em=object0.5em(self)We use result as an accumulator.0.5em0.5eminherit0.5em[’visitor]0.5emlambdavisit0.5em0.5emmethod0.5emvisitVar0.5emvar0.5em=0.5em0.5em0.5em0.5emresult0.5em:=0.5emvar#v0.5em::0.5em!result0.5em0.5emmethod0.5emvisitAbs0.5emabs0.5em=0.5em0.5em0.5em0.5em(abs#body)#accept0.5emself;0.5em0.5em0.5em0.5emresult0.5em:=0.5emList.filter0.5em(fun0.5emv’0.5em->0.5emv’0.5em<>0.5emabs#v)0.5em!result0.5em0.5emmethod0.5emvisitApp0.5emapp0.5em=0.5em0.5em0.5em0.5emapp#arg#accept0.5emself;0.5emapp#f#accept0.5emselfendtype0.5emlambdavisitt0.5em=0.5emlambdavisitt0.5emlambdavisitVisitor for the language of \lambda-expressions.type0.5emlambdat0.5em=0.5emlambdavisitt0.5emvisitablelet0.5emeval10.5em(e0.5em:0.5emlambdat)0.5emsubst0.5em:0.5emlambdat0.5em=0.5em0.5emlet0.5emresult0.5em=0.5emref0.5em(newvar0.5em”“)0.5eminThis initial value will be ignored.0.5em0.5eme#accept0.5em(new0.5emevallambda0.5emsubst0.5emresult0.5em:>0.5emlambdavisitt);0.5em0.5em!resultlet0.5emfreevars10.5em(e0.5em:0.5emlambdat)0.5em=0.5em0.5emlet0.5emresult0.5em=0.5emref0.5em[]0.5eminInitial value of the accumulator.0.5em0.5eme#accept0.5em(new0.5emfreevarslambda0.5emresult);0.5em0.5em!resultlet0.5emtest10.5em=0.5em0.5em(newapp0.5em(newabs0.5em”x”0.5em(newvar0.5em”x”))0.5em(newvar0.5em”y”)0.5em:>0.5emlambdat)let0.5emetest0.5em=0.5emeval10.5emtest10.5em[]let0.5emfvtest0.5em=0.5emfreevars10.5emtest1class0.5em[’visitor]0.5emnum0.5em(i0.5em:0.5emint)0.5em=object0.5em(self)0.5em0.5emmethod0.5emi0.5em=0.5emi0.5em0.5emmethod0.5emaccept0.5em:0.5em’visitor0.5em->0.5emunit0.5em=0.5em0.5em0.5em0.5emfun0.5emvisitor0.5em->0.5emvisitor#visitNum0.5emselfendlet0.5emnewnum0.5emi0.5em=0.5em(new0.5emnum0.5emi0.5em:>0.5em’a0.5emvisitable)class0.5emvirtual0.5em[’visitor]0.5emoperation0.5em0.5em(arg10.5em:0.5em’visitor0.5emvisitable)0.5em(arg20.5em:0.5em’visitor0.5emvisitable)0.5em=object0.5em(self)Shared accessor methods.0.5em0.5emmethod0.5emarg10.5em=0.5emarg10.5em0.5emmethod0.5emarg20.5em=0.5emarg2endclass0.5em[’visitor]0.5emadd0.5emarg10.5emarg20.5em=object0.5em(self)0.5em0.5eminherit0.5em[’visitor]0.5emoperation0.5emarg10.5emarg20.5em0.5emmethod0.5emaccept0.5em:0.5em’visitor0.5em->0.5emunit0.5em=0.5em0.5em0.5em0.5emfun0.5emvisitor0.5em->0.5emvisitor#visitAdd0.5emselfendlet0.5emnewadd0.5emarg10.5emarg20.5em=0.5em(new0.5emadd0.5emarg10.5emarg20.5em:>0.5em’a0.5emvisitable)class0.5em[’visitor]0.5emmult0.5emarg10.5emarg20.5em=object0.5em(self)0.5em0.5eminherit0.5em[’visitor]0.5emoperation0.5emarg10.5emarg20.5em0.5emmethod0.5emaccept0.5em:0.5em’visitor0.5em->0.5emunit0.5em=0.5em0.5em0.5em0.5emfun0.5emvisitor0.5em->0.5emvisitor#visitMult0.5emselfendlet0.5emnewmult0.5emarg10.5emarg20.5em=0.5em(new0.5emmult0.5emarg10.5emarg20.5em:>0.5em’a0.5emvisitable)class0.5emvirtual0.5em[’visitor]0.5emexprvisit0.5em=The sub-language of arithmetic expressions.object0.5em0.5emmethod0.5emvirtual0.5emvisitNum0.5em:0.5em’visitor0.5emnum0.5em->0.5emunit0.5em0.5emmethod0.5emvirtual0.5emvisitAdd0.5em:0.5em’visitor0.5emadd0.5em->0.5emunit0.5em0.5emmethod0.5emvirtual0.5emvisitMult0.5em:0.5em’visitor0.5emmult0.5em->0.5emunitendclass0.5em[’visitor]0.5emevalexpr0.5em0.5em(result0.5em:0.5em’visitor0.5emvisitable0.5emref)0.5em=object0.5em(self)0.5em0.5eminherit0.5em[’visitor]0.5emexprvisit0.5em0.5emval0.5emmutable0.5emnumredex0.5em:0.5emint0.5emoption0.5em=0.5emNoneThe numeric result, if any.0.5em0.5emmethod0.5emvisitNum0.5emnum0.5em=0.5em0.5em0.5em0.5emnumredex0.5em<-0.5emSome0.5emnum#i;0.5em0.5em0.5em0.5emresult0.5em:=0.5em(num0.5em:>0.5em’visitor0.5emvisitable)0.5em0.5emmethod0.5emprivate0.5emvisitOperation0.5emnewe0.5emop0.5eme0.5em=0.5em0.5em0.5em0.5em(e#arg1)#accept0.5emself;0.5em0.5em0.5em0.5emlet0.5emarg1’0.5em=0.5em!result0.5emand0.5emi10.5em=0.5emnumredex0.5emin0.5em0.5em0.5em0.5em(e#arg2)#accept0.5emself;0.5em0.5em0.5em0.5emlet0.5emarg2’0.5em=0.5em!result0.5emand0.5emi20.5em=0.5emnumredex0.5emin0.5em0.5em0.5em0.5emmatch0.5emi1,0.5emi20.5emwith0.5em0.5em0.5em0.5em0.5emSome0.5emi1,0.5emSome0.5emi20.5em->0.5em0.5em0.5em0.5em0.5em0.5emlet0.5emres0.5em=0.5emop0.5emi10.5emi20.5emin0.5em0.5em0.5em0.5em0.5em0.5emnumredex0.5em<-0.5emSome0.5emres;0.5emresult0.5em:=0.5emnewnum0.5emres0.5em0.5em0.5em0.5em->0.5em0.5em0.5em0.5em0.5em0.5emnumredex0.5em<-0.5emNone;0.5em0.5em0.5em0.5em0.5em0.5emresult0.5em:=0.5emnewe0.5emarg1’0.5emarg2’0.5em0.5emmethod0.5emvisitAdd0.5emadd0.5em=0.5emself#visitOperation0.5emnewadd0.5em(0.5em+0.5em)0.5emadd0.5em0.5emmethod0.5emvisitMult0.5emmult0.5em=0.5emself#visitOperation0.5emnewmult0.5em(0.5em*0.5em)0.5emmultendclass0.5em[’visitor]0.5emfreevarsexpr0.5em(result0.5em:0.5emvarname0.5emlist0.5emref)0.5em=Flow-through classobject0.5em(self)for computing free variables.0.5em0.5eminherit0.5em[’visitor]0.5emexprvisit0.5em0.5emmethod0.5emvisitNum=0.5em()0.5em0.5emmethod0.5emvisitAdd0.5emadd0.5em=0.5em0.5em0.5em0.5emadd#arg1#accept0.5emself;0.5emadd#arg2#accept0.5emself0.5em0.5emmethod0.5emvisitMult0.5emmult0.5em=0.5em0.5em0.5em0.5emmult#arg1#accept0.5emself;0.5emmult#arg2#accept0.5emselfendtype0.5emexprvisitt0.5em=0.5emexprvisitt0.5emexprvisitThe language of arithmetic expressionstype0.5emexprt0.5em=0.5emexprvisitt0.5emvisitable– in this example without variables.let0.5emeval20.5em(e0.5em:0.5emexprt)0.5em:0.5emexprt0.5em=0.5em0.5emlet0.5emresult0.5em=0.5emref0.5em(newnum0.5em0)0.5eminThis initial value will be ignored.0.5em0.5eme#accept0.5em(new0.5emevalexpr0.5emresult);0.5em0.5em!resultlet0.5emtest20.5em=0.5em0.5em(newadd0.5em(newmult0.5em(newnum0.5em3)0.5em(newnum0.5em3))0.5em(newnum0.5em1)0.5em:>0.5emexprt)let0.5emetest0.5em=0.5emeval20.5emtest2class0.5emvirtual0.5em[’visitor]0.5emlexprvisit0.5em=Combining the variants / constructors.object0.5em0.5eminherit0.5em[’visitor]0.5emlambdavisit0.5em0.5eminherit0.5em[’visitor]0.5emexprvisitendclass0.5em[’visitor]0.5emevallexpr0.5emsubst0.5emresult0.5em=Combining the ‘‘pattern-matching branches’’.object0.5em0.5eminherit0.5em[’visitor]0.5emevalexpr0.5emresult0.5em0.5eminherit0.5em[’visitor]0.5emevallambda0.5emsubst0.5emresultendclass0.5em[’visitor]0.5emfreevarslexpr0.5emresult0.5em=object0.5em0.5eminherit0.5em[’visitor]0.5emfreevarsexpr0.5emresult0.5em0.5eminherit0.5em[’visitor]0.5emfreevarslambda0.5emresultendtype0.5emlexprvisitt0.5em=0.5emlexprvisitt0.5emlexprvisitThe language combiningtype0.5emlexprt0.5em=0.5emlexprvisitt0.5emvisitable\lambda-expressions and arithmetic expressions.let0.5emeval30.5em(e0.5em:0.5emlexprt)0.5emsubst0.5em:0.5emlexprt0.5em=0.5em0.5emlet0.5emresult0.5em=0.5emref0.5em(newnum0.5em0)0.5emin0.5em0.5eme#accept0.5em(new0.5emevallexpr0.5emsubst0.5emresult);0.5em0.5em!resultlet0.5emfreevars30.5em(e0.5em:0.5emlexprt)0.5em=0.5em0.5emlet0.5emresult0.5em=0.5emref0.5em[]0.5emin0.5em0.5eme#accept0.5em(new0.5emfreevarslexpr0.5emresult);0.5em0.5em!resultlet0.5emtest30.5em=0.5em0.5em(newadd0.5em(newmult0.5em(newnum0.5em3)0.5em(newvar0.5em”x”))0.5em(newnum0.5em1)0.5em:>0.5emlexprt)let0.5emetest0.5em=0.5emeval30.5emtest30.5em[]let0.5emfvtest0.5em=0.5emfreevars30.5emtest3let0.5emoldetest0.5em=0.5emeval30.5em(test20.5em:>0.5emlexprt)0.5em[]let0.5emoldfvtest0.5em=0.5emeval30.5em(test20.5em:>0.5emlexprt)0.5em[]Polymorphic Variant Types: Subtyping

   • Polymorphic variants are to ordinary variants as objects are to records: both enable open types and subtyping, both allow different types to share the same components.

     • They are dual concepts in that if we replace “product” of records / objects by “sum” (see lecture 2), we get variants / polymorphic variants.Duality implies many behaviors are opposite.

   • While object subtypes have more methods, polymorphic variant subtypes have less tags.

   • The > sign means “these tags or more”:

     let0.5eml0.5em=0.5em[’Int0.5em3;0.5em‘Float0.5em4.];;val0.5eml0.5em:0.5em[>0.5em‘Float0.5emof0.5emfloat0.5em0.5em‘Int0.5emof0.5emint0.5em]0.5emlist0.5em=0.5em[’Int0.5em3;0.5em‘Float0.5em4.]

   • The < sign means “these tags or less”:

     let0.5emispositive0.5em=0.5emfunction0.5em0.5em0.5em0.5em0.5em0.5em‘Int0.5em0.5em0.5emx0.5em->0.5emSome0.5em(x0.5em>0.5em0)0.5em0.5em0.5em0.5em0.5em0.5em‘Float0.5emx0.5em->0.5emSome0.5em(x0.5em>0.5em0.)0.5em0.5em0.5em0.5em0.5em0.5em‘Notanumber0.5em->0.5emNone;;val0.5emispositive0.5em:0.5em0.5em[<0.5em‘Float0.5emof0.5emfloat0.5em0.5em‘Int0.5emof0.5emint0.5em0.5em‘Notanumber0.5em]0.5em->0.5em bool0.5emoption0.5em=0.5em

   • No sign means a closed type (similar to an object type without the ..)

   • Both an upper and a lower bound are sometimes inferred,see https://realworldocaml.org/v1/en/html/variants.html

     List.filter0.5em0.5em(fun0.5emx0.5em->0.5emmatch0.5emispositive0.5emx0.5emwith0.5emNone0.5em->0.5emfalse0.5em0.5emSome0.5emb0.5em->0.5emb)0.5eml;;-0.5em:0.5em[<0.5em‘Float0.5emof0.5emfloat0.5em0.5em‘Int0.5emof0.5emint0.5em0.5em‘Notanumber0.5em>0.5em‘Float0.5em‘Int0.5em]0.5em list0.5em=[’Int0.5em3;0.5em‘Float0.5em4.]Polymorphic Variant Types: The Expression Problem

   • Because distinct polymorphic variant types can share the same tags, the solution to the Expression Problem is straightforward.

   • Penalty points:

     • The need to “tie the recursive knot” separately both at the type level and the function level. At the function level, an \eta-expansion is required due to value recursion problem. At the type level, the type variable can be confusing.
     • There can be a slight time cost compared to the visitor pattern-based approach: additional dispatch at each level of type aggregation (i.e.  merging sub-languages).

     Verdict: a flexible and concise solution, second-best place.

   type0.5emvar0.5em=0.5em[’Var0.5emof0.5emstring]let0.5emevalvar0.5emsub0.5em(’Var0.5ems0.5emas0.5emv0.5em:0.5emvar)0.5em=0.5em0.5emtry0.5emList.assoc0.5ems0.5emsub0.5emwith0.5emNotfound0.5em->0.5emvtype0.5em’a0.5emlambda0.5em=0.5em0.5em[’Var0.5emof0.5emstring0.5em0.5em‘Abs0.5emof0.5emstring0.5em0.5em’a0.5em0.5em‘App0.5emof0.5em’a0.5em0.5em’a]let0.5emgensym0.5em=0.5emlet0.5emn0.5em=0.5emref0.5em00.5emin0.5emfun0.5em()0.5em->0.5emincr0.5emn;0.5em”“0.5em0.5emstringofint0.5em!nlet0.5emevallambda0.5emevalrec0.5emsubst0.5em:0.5em’a0.5emlambda0.5em->0.5em’a0.5em=0.5emfunction0.5em0.5em0.5em#var0.5emas0.5emv0.5em->0.5emevalvar0.5emsubst0.5emvWe could also leave the type open0.5em0.5em0.5em‘App0.5em(l1,0.5eml2)0.5em->rather than closing it to lambda.0.5em0.5em0.5em0.5emlet0.5eml2’0.5em=0.5emevalrec0.5emsubst0.5eml20.5emin0.5em0.5em0.5em0.5em(match0.5emevalrec0.5emsubst0.5eml10.5emwith0.5em0.5em0.5em0.5em0.5em‘Abs0.5em(s,0.5embody)0.5em->0.5em0.5em0.5em0.5em0.5em0.5emevalrec0.5em[s,0.5eml2’]0.5embody0.5em0.5em0.5em0.5em0.5eml1’0.5em->0.5em‘App0.5em(l1’,0.5eml2’))0.5em0.5em0.5em‘Abs0.5em(s,0.5eml1)0.5em->0.5em0.5em0.5em0.5emlet0.5ems’0.5em=0.5emgensym0.5em()0.5emin0.5em0.5em0.5em0.5em‘Abs0.5em(s’,0.5emevalrec0.5em((s,0.5em‘Var0.5ems’)::subst)0.5eml1)let0.5emfreevarslambda0.5emfreevarsrec0.5em:0.5em’a0.5emlambda0.5em->0.5em’b0.5em=0.5emfunction0.5em0.5em0.5em‘Var0.5emv0.5em->0.5em[v]0.5em0.5em0.5em‘App0.5em(l1,0.5eml2)0.5em->0.5emfreevarsrec0.5eml10.5em@0.5emfreevarsrec0.5eml20.5em0.5em0.5em‘Abs0.5em(s,0.5eml1)0.5em->0.5em0.5em0.5em0.5emList.filter0.5em(fun0.5emv0.5em->0.5emv0.5em<>0.5ems)0.5em(freevarsrec0.5eml1)type0.5emlambdat0.5em=0.5emlambdat0.5emlambdalet0.5emrec0.5emeval10.5emsubst0.5eme0.5em:0.5emlambdat0.5em=0.5emevallambda0.5emeval10.5emsubst0.5emelet0.5emrec0.5emfreevars10.5em(e0.5em:0.5emlambdat)0.5em=0.5emfreevarslambda0.5emfreevars10.5emelet0.5emtest10.5em=0.5em(’App0.5em(’Abs0.5em(”x”,0.5em‘Var0.5em”x”),0.5em‘Var0.5em”y”)0.5em:>0.5emlambdat)let0.5emetest0.5em=0.5emeval10.5em[]0.5emtest1let0.5emfvtest0.5em=0.5emfreevars10.5emtest1type0.5em’a0.5emexpr0.5em=0.5em0.5em[’Var0.5emof0.5emstring0.5em0.5em‘Num0.5emof0.5emint0.5em0.5em‘Add0.5emof0.5em’a0.5em0.5em’a0.5em0.5em‘Mult0.5emof0.5em’a0.5em0.5em’a]let0.5emmapexpr0.5em(f0.5em:0.5em0.5em->0.5em’a)0.5em:0.5em’a0.5emexpr0.5em->0.5em’a0.5em=0.5emfunction0.5em0.5em0.5em#var0.5emas0.5emv0.5em->0.5emv0.5em0.5em0.5em‘Num0.5em0.5emas0.5emn0.5em->0.5emn0.5em0.5em0.5em‘Add0.5em(e1,0.5eme2)0.5em->0.5em‘Add0.5em(f0.5eme1,0.5emf0.5eme2)0.5em0.5em0.5em‘Mult0.5em(e1,0.5eme2)0.5em->0.5em‘Mult0.5em(f0.5eme1,0.5emf0.5eme2)let0.5emevalexpr0.5emevalrec0.5emsubst0.5em(e0.5em:0.5em’a0.5emexpr)0.5em:0.5em’a0.5em=0.5em0.5emmatch0.5emmapexpr0.5em(evalrec0.5emsubst)0.5eme0.5emwith0.5em0.5em0.5em#var0.5emas0.5emv0.5em->0.5emevalvar0.5emsubst0.5emvHere and elsewhere, we could also factor-out0.5em0.5em0.5em‘Add0.5em(’Num0.5emm,0.5em‘Num0.5emn)0.5em->0.5em‘Num0.5em(m0.5em+0.5emn)the sub-language of variables.0.5em0.5em0.5em‘Mult0.5em(’Num0.5emm,0.5em‘Num0.5emn)0.5em->0.5em‘Num0.5em(m0.5em*0.5emn)0.5em0.5em0.5eme0.5em->0.5emelet0.5emfreevarsexpr0.5emfreevarsrec0.5em:0.5em’a0.5emexpr0.5em->0.5em’b0.5em=0.5emfunction0.5em0.5em0.5em‘Var0.5emv0.5em->0.5em[v]0.5em0.5em0.5em‘Num0.5em0.5em->0.5em[]0.5em0.5em0.5em‘Add0.5em(e1,0.5eme2)0.5em0.5em‘Mult0.5em(e1,0.5eme2)0.5em->0.5emfreevarsrec0.5eme10.5em@0.5emfreevarsrec0.5eme2type0.5emexprt0.5em=0.5emexprt0.5emexprlet0.5emrec0.5emeval20.5emsubst0.5eme0.5em:0.5emexprt0.5em=0.5emevalexpr0.5emeval20.5emsubst0.5emelet0.5emrec0.5emfreevars20.5em(e0.5em:0.5emexprt)0.5em=0.5emfreevarsexpr0.5emfreevars20.5emelet0.5emtest20.5em=0.5em(’Add0.5em(’Mult0.5em(’Num0.5em3,0.5em‘Var0.5em”x”),0.5em‘Num0.5em1)0.5em:0.5emexprt)let0.5emetest20.5em=0.5emeval20.5em[“x”,0.5em‘Num0.5em2]0.5emtest2let0.5emfvtest20.5em=0.5emfreevars20.5emtest2type0.5em’a0.5emlexpr0.5em=0.5em[’a0.5emlambda0.5em0.5em’a0.5emexpr]let0.5emevallexpr0.5emevalrec0.5emsubst0.5em:0.5em’a0.5emlexpr0.5em->0.5em’a0.5em=0.5emfunction0.5em0.5em0.5em#lambda0.5emas0.5emx0.5em->0.5emevallambda0.5emevalrec0.5emsubst0.5emx0.5em0.5em0.5em#expr0.5emas0.5emx0.5em->0.5emevalexpr0.5emevalrec0.5emsubst0.5emxlet0.5emfreevarslexpr0.5emfreevarsrec0.5em:0.5em’a0.5emlexpr0.5em->0.5em’b0.5em=0.5emfunction0.5em0.5em0.5em#lambda0.5emas0.5emx0.5em->0.5emfreevarslambda0.5emfreevarsrec0.5emx0.5em0.5em0.5em#expr0.5emas0.5emx0.5em->0.5emfreevarsexpr0.5emfreevarsrec0.5emxtype0.5emlexprt0.5em=0.5emlexprt0.5emlexprlet0.5emrec0.5emeval30.5emsubst0.5eme0.5em:0.5emlexprt0.5em=0.5emevallexpr0.5emeval30.5emsubst0.5emelet0.5emrec0.5emfreevars30.5em(e0.5em:0.5emlexprt)0.5em=0.5emfreevarslexpr0.5emfreevars30.5emelet0.5emtest30.5em=0.5em0.5em(’App0.5em(’Abs0.5em(“x”,0.5em‘Add0.5em(’Mult0.5em(’Num0.5em3,0.5em‘Var0.5em”x”),0.5em‘Num0.5em1)),0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em‘Num0.5em2)0.5em:0.5emlexprt)let0.5emetest30.5em=0.5emeval30.5em[]0.5emtest3let0.5emfvtest30.5em=0.5emfreevars30.5emtest3let0.5emeoldtest0.5em=0.5emeval30.5em[]0.5em(test20.5em:>0.5emlexprt)let0.5emfvoldtest0.5em=0.5emfreevars30.5em(test20.5em:>0.5emlexprt)Polymorphic Variants and Recursive Modules

   • Using recursive modules, we can clean-up the confusing or cluttering aspects of tying the recursive knots: type variables, recursive call arguments.
   • We need private types, which for objects and polymorphic variants means private rows.

     • We can conceive of open row types, e.g. [> ’Int0.5emof0.5emint0.5em0.5em‘String0.5emof0.5emstring] as using a row variable, e.g. 'a:

       [’Int0.5emof0.5emint0.5em0.5em‘String0.5emof0.5emstring0.5em0.5em’a]

       and then of private row types as abstracting the row variable:

       type0.5emtrowtype0.5emt0.5em=0.5em[’Int0.5emof0.5emint0.5em0.5em‘String0.5emof0.5emstring0.5em0.5emtrow]

       But the actual formalization of private row types is more complex.

   • Penalty points:
     • We still need to tie the recursive knots for types, for example private0.5em[>0.5em’a0.5emlambda]0.5emas0.5em’a.
     • There can be slight time costs due to the use of functors and dispatch on merging of sub-languages.
   • Verdict: a clean solution, best place.

   type0.5emvar0.5em=0.5em[’Var0.5emof0.5emstring]let0.5emevalvar0.5emsubst0.5em(’Var0.5ems0.5emas0.5emv0.5em:0.5emvar)0.5em=0.5em0.5emtry0.5emList.assoc0.5ems0.5emsubst0.5emwith0.5emNotfound0.5em->0.5emvtype0.5em’a0.5emlambda0.5em=0.5em0.5em[’Var0.5emof0.5emstring0.5em0.5em‘Abs0.5emof0.5emstring0.5em0.5em’a0.5em0.5em‘App0.5emof0.5em’a0.5em0.5em’a]module0.5emtype0.5emEval0.5em=sig0.5emtype0.5emexp0.5emval0.5emeval0.5em:0.5em(string0.5em*0.5emexp)0.5emlist0.5em->0.5emexp0.5em->0.5emexp0.5emendmodule0.5emLF(X0.5em:0.5emEval0.5emwith0.5emtype0.5emexp0.5em=0.5emprivate0.5em[>0.5em’a0.5emlambda]0.5emas0.5em’a)0.5em=struct0.5em0.5emtype0.5emexp0.5em=0.5emX.exp0.5emlambda0.5em0.5emlet0.5emgensym0.5em=0.5em

   let0.5emn0.5em=0.5emref0.5em00.5emin0.5emfun0.5em()0.5em->0.5emincr0.5emn;0.5em”“0.5em0.5emstringofint0.5em!n0.5em0.5emlet0.5emeval0.5emsubst0.5em:0.5emexp0.5em->0.5emX.exp0.5em=0.5emfunction0.5em0.5em0.5em0.5em0.5em#var0.5emas0.5emv0.5em->0.5emevalvar0.5emsubst0.5emv0.5em0.5em0.5em0.5em0.5em‘App0.5em(l1,0.5eml2)0.5em->0.5em0.5em0.5em0.5em0.5em0.5emlet0.5eml2’0.5em=0.5emX.eval0.5emsubst0.5eml20.5emin0.5em0.5em0.5em0.5em0.5em0.5em(match0.5emX.eval0.5emsubst0.5eml10.5emwith0.5em0.5em0.5em0.5em0.5em0.5em0.5em‘Abs0.5em(s,0.5embody)0.5em->0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5emX.eval0.5em[s,0.5eml2’]0.5embody0.5em0.5em0.5em0.5em0.5em0.5em0.5eml1’0.5em->0.5em‘App0.5em(l1’,0.5eml2’))0.5em0.5em0.5em0.5em0.5em‘Abs0.5em(s,0.5eml1)0.5em->0.5em0.5em0.5em0.5em0.5em0.5emlet0.5ems’0.5em=0.5emgensym0.5em()0.5emin0.5em0.5em0.5em0.5em0.5em0.5em‘Abs0.5em(s’,0.5emX.eval0.5em((s,0.5em‘Var0.5ems’)::subst)0.5eml1)endmodule0.5emrec0.5emLambda0.5em:0.5em(Eval0.5emwith0.5emtype0.5emexp0.5em=0.5emLambda.exp0.5emlambda)0.5em=0.5em0.5emLF(Lambda)module0.5emtype0.5emFreeVars0.5em=sig0.5emtype0.5emexp0.5emval0.5emfreevars0.5em:0.5emexp0.5em->0.5emstring0.5emlist0.5emendmodule0.5emLFVF(X0.5em:0.5emFreeVars0.5emwith0.5emtype0.5emexp0.5em=0.5emprivate0.5em[>0.5em’a0.5emlambda]0.5emas0.5em’a)0.5em=struct0.5em0.5emtype0.5emexp0.5em=0.5emX.exp0.5emlambda0.5em0.5emlet0.5emfreevars0.5em:0.5emexp0.5em->0.5em’b0.5em=0.5emfunction0.5em0.5em0.5em0.5em0.5em‘Var0.5emv0.5em->0.5em[v]0.5em0.5em0.5em0.5em0.5em‘App0.5em(l1,0.5eml2)0.5em->0.5emX.freevars0.5eml10.5em@0.5emX.freevars0.5eml20.5em0.5em0.5em0.5em0.5em‘Abs0.5em(s,0.5eml1)0.5em->0.5em0.5em0.5em0.5em0.5em0.5emList.filter0.5em(fun0.5emv0.5em->0.5emv0.5em<>0.5ems)0.5em(X.freevars0.5eml1)endmodule0.5emrec0.5emLambdaFV0.5em:0.5em(FreeVars0.5emwith0.5emtype0.5emexp0.5em=0.5emLambdaFV.exp0.5emlambda)0.5em=0.5em0.5emLFVF(LambdaFV)let0.5emtest10.5em=0.5em(’App0.5em(’Abs0.5em(”x”,0.5em‘Var0.5em”x”),0.5em‘Var0.5em”y”)0.5em:0.5emLambda.exp)let0.5emetest0.5em=0.5emLambda.eval0.5em[]0.5emtest1let0.5emfvtest0.5em=0.5emLambdaFV.freevars0.5emtest1type0.5em’a0.5emexpr0.5em=0.5em0.5em[’Var0.5emof0.5emstring0.5em0.5em‘Num0.5emof0.5emint0.5em0.5em‘Add0.5emof0.5em’a0.5em0.5em’a0.5em0.5em‘Mult0.5emof0.5em’a0.5em0.5em’a]module0.5emtype0.5emOperations0.5em=sig0.5eminclude0.5emEval0.5eminclude0.5emFreeVars0.5emwith0.5emtype0.5emexp0.5em:=0.5emexp0.5emendmodule0.5emEF(X0.5em:0.5emOperations0.5emwith0.5emtype0.5emexp0.5em=0.5emprivate0.5em[>0.5em’a0.5emexpr]0.5emas0.5em’a)0.5em=struct0.5em0.5emtype0.5emexp0.5em=0.5emX.exp0.5emexpr0.5em0.5emlet0.5emmapexpr0.5emf0.5em=0.5emfunction0.5em0.5em0.5em0.5em0.5em#var0.5emas0.5emv0.5em->0.5emv0.5em0.5em0.5em0.5em0.5em‘Num0.5em0.5emas0.5emn0.5em->0.5emn0.5em0.5em0.5em0.5em0.5em‘Add0.5em(e1,0.5eme2)0.5em->0.5em‘Add0.5em(f0.5eme1,0.5emf0.5eme2)0.5em0.5em0.5em0.5em0.5em‘Mult0.5em(e1,0.5eme2)0.5em->0.5em‘Mult0.5em(f0.5eme1,0.5emf0.5eme2)0.5em0.5emlet0.5emeval0.5emsubst0.5em(e0.5em:0.5emexp)0.5em:0.5emX.exp0.5em=0.5em0.5em0.5em0.5emmatch0.5emmapexpr0.5em(X.eval0.5emsubst)0.5eme0.5emwith0.5em0.5em0.5em0.5em0.5em#var0.5emas0.5emv0.5em->0.5emevalvar0.5emsubst0.5emv0.5em0.5em0.5em0.5em0.5em‘Add0.5em(’Num0.5emm,0.5em‘Num0.5emn)0.5em->0.5em‘Num0.5em(m0.5em+0.5emn)0.5em0.5em0.5em0.5em0.5em‘Mult0.5em(’Num0.5emm,0.5em‘Num0.5emn)0.5em->0.5em‘Num0.5em(m0.5em*0.5emn)0.5em0.5em0.5em0.5em0.5eme0.5em->0.5eme0.5em0.5emlet0.5emfreevars0.5em:0.5emexp0.5em->0.5em’b0.5em=0.5emfunction0.5em0.5em0.5em0.5em0.5em‘Var0.5emv0.5em->0.5em[v]0.5em0.5em0.5em0.5em0.5em‘Num0.5em0.5em->0.5em[]0.5em0.5em0.5em0.5em0.5em‘Add0.5em(e1,0.5eme2)0.5em0.5em‘Mult0.5em(e1,0.5eme2)0.5em->0.5emX.freevars0.5eme10.5em@0.5emX.freevars0.5eme2endmodule0.5emrec0.5emExpr0.5em:0.5em(Operations0.5emwith0.5emtype0.5emexp0.5em=0.5emExpr.exp0.5emexpr)0.5em=0.5em0.5emEF(Expr)let0.5emtest20.5em=0.5em(’Add0.5em(’Mult0.5em(’Num0.5em3,0.5em‘Var0.5em”x”),0.5em‘Num0.5em1)0.5em:0.5emExpr.exp)let0.5emetest20.5em=0.5emExpr.eval0.5em[“x”,0.5em‘Num0.5em2]0.5emtest2let0.5emfvstest20.5em=0.5emExpr.freevars0.5emtest2type0.5em’a0.5emlexpr0.5em=0.5em[’a0.5emlambda0.5em0.5em’a0.5emexpr]module0.5emLEF(X0.5em:0.5emOperations0.5emwith0.5emtype0.5emexp0.5em=0.5emprivate0.5em[>0.5em’a0.5emlexpr]0.5emas0.5em’a)0.5em=struct0.5em0.5emtype0.5emexp0.5em=0.5emX.exp0.5emlexpr0.5em0.5emmodule0.5emLambdaX0.5em=0.5emLF(X)0.5em0.5emmodule0.5emLambdaFVX0.5em=0.5emLFVF(X)0.5em0.5emmodule0.5emExprX0.5em=0.5emEF(X)0.5em0.5emlet0.5emeval0.5emsubst0.5em:0.5emexp0.5em->0.5emX.exp0.5em=0.5emfunction0.5em0.5em0.5em0.5em0.5em#LambdaX.exp0.5emas0.5emx0.5em->0.5emLambdaX.eval0.5emsubst0.5emx0.5em0.5em0.5em0.5em0.5em#ExprX.exp0.5emas0.5emx0.5em->0.5emExprX.eval0.5emsubst0.5emx0.5em0.5emlet0.5emfreevars0.5em:0.5emexp0.5em->0.5em’b0.5em=0.5emfunction0.5em0.5em0.5em0.5em0.5em#lambda0.5emas0.5emx0.5em->0.5emLambdaFVX.freevars0.5emxEither of #lambda or #LambdaX.exp is fine.0.5em0.5em0.5em0.5em0.5em#expr0.5emas0.5emx0.5em->0.5emExprX.freevars0.5emxEither of #expr or #ExprX.exp is fine.endmodule0.5emrec0.5emLExpr0.5em:0.5em(Operations0.5emwith0.5emtype0.5emexp0.5em=0.5emLExpr.exp0.5emlexpr)0.5em=0.5em0.5emLEF(LExpr)let0.5emtest30.5em=0.5em0.5em(’App0.5em(’Abs0.5em(“x”,0.5em‘Add0.5em(’Mult0.5em(’Num0.5em3,0.5em‘Var0.5em”x”),0.5em‘Num0.5em1)),0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em‘Num0.5em2)0.5em:0.5emLExpr.exp)let0.5emetest30.5em=0.5emLExpr.eval0.5em[]0.5emtest3let0.5emfvtest30.5em=0.5emLExpr.freevars0.5emtest3let0.5emeoldtest0.5em=0.5emLExpr.eval0.5em[]0.5em(test20.5em:>0.5emLExpr.exp)let0.5emfvoldtest0.5em=0.5emLExpr.freevars0.5em(test20.5em:>0.5emLExpr.exp)Digression: Parser Combinators

   • We have done parsing using external languages OCamlLex and Menhir, now we will look at parsers written directly in OCaml.

   • Language combinators are ways defining languages by composing definitions of smaller languages. For example, the combinators of the Extended Backus-Naur Form notation are:

     • concatenation: S = A, B stands for S = \lbrace a b|a \in A, b \in b \rbrace,
     • alternation: S = A|B stands for S = \lbrace a|a \in A \vee a \in B \rbrace,
     • option: S = [A] stands for S = \lbrace \epsilon \rbrace \cup A, where \epsilon is an empty string,
     • repetition: S = \lbrace A \rbrace stands for S = \lbrace \epsilon \rbrace \cup \lbrace a s|a \in A, s \in S \rbrace,
     • terminal string: S ='' a'' stands for S = \lbrace a \rbrace.

   • Parsers implemented directly in a functional programming paradigm are functions from character streams to the parsed values. Algorithmically they are recursive descent parsers.

   • Parser combinators approach builds parsers as monad plus values:

     • Bind: val (>>=) : 'a parser -> ('a -> 'b parser) -> 'b parser

       • p >>= f is a parser that first parses p, and makes the result available for parsing f.

     • Return: val return : 'a -> 'a parser

       • return x parses an empty string, symbolically S = \lbrace \epsilon \rbrace, and returns x.

     • MZero: val fail : 'a parser

       • fail fails to parse anything, symbolically S = \varnothing = \lbrace \rbrace.

     • MPlus: either val <|> : 'a parser -> 'a parser -> 'a parser,

       or val <|> : 'a parser -> 'b parser -> ('a, 'b) choice parser

       • p <|> q tries p, and if p succeeds, its result is returned, otherwise the parser q is used.

     The only non-monad-plus operation that has to be built into the monad is some way to consume a single character from the input stream, for example:

     • val satisfy : (char -> bool) -> char parser
       • satisfy (fun c -> c = 'a') consumes the character “a” from the input stream and returns it; if the input stream starts with a different character, this parser fails.

   • Ordinary monadic recursive descent parsers do not allow left-recursion: if a cycle of calls not consuming any character can be entered when a parse failure should occur, the cycle will keep repeating.

     • For example, if we define numbers N := D | N D, where D stands for digits, then a stack of uses of the rule N \rightarrow N D will build up when the next character is not a digit.
     • On the other hand, rules can share common prefixes.Parser Combinators: Implementation

   • The parser monad is actually a composition of two monads:

     • the state monad for storing the stream of characters that remain to be parsed,
     • the backtracking monad for handling parse failures and ambiguities.

     Alternatively, one can split the state monad into a reader monad with the parsed string, and a state monad with the parsing position.

   • Recall Lecture 8, especially slides 54-63.

   • On my new OPAM installation of OCaml, I run the parsing example with:

     ocamlbuild Plugin1.cmxs -pp "camlp4o /home/lukstafi/.opam/4.02.1/lib/monad-custom/pa_monad.cmo"

     ocamlbuild Plugin2.cmxs -pp "camlp4o /home/lukstafi/.opam/4.02.1/lib/monad-custom/pa_monad.cmo"

     ocamlbuild PluginRun.native -lib dynlink -pp "camlp4o ~/.opam/4.02.1/lib/monad-custom/pa_monad.cmo" -- "(3*(6+1))" _build/Plugin1.cmxs _build/Plugin2.cmxs

   • We experiment with a different approach to monad-plus. The merits of this approach (or lack thereof) is left as an exercise. lazy-monad-plus:

     val0.5emmplus0.5em:0.5em’a0.5emmonad ->0.5em’a0.5emmonad0.5emLazy.t0.5em->0.5em’a0.5emmonad

   Parser Combinators: Implementation of lazy-monad-plus

   • Excerpts from Monad.ml. First an operation from MonadPlusOps.

   0.5em0.5emlet0.5emmsummap0.5emf0.5eml0.5em=0.5em0.5em0.5em0.5emList.foldleftFolding left reversers the apparent order of composition,0.5em0.5em0.5em0.5em0.5em0.5em(fun0.5emacc0.5ema0.5em->0.5emmplus0.5emacc0.5em(lazy0.5em(f0.5ema)))0.5emmzero0.5emlorder from l is preserved.

   • The implementation of the lazy-monad-plus.

   type0.5em’a0.5emllist0.5em=0.5emLNil0.5em0.5emLCons0.5emof0.5em’a0.5em0.5em’a0.5emllist0.5emLazy.tlet0.5emrec0.5emltake0.5emn0.5em=0.5emfunction0.5em0.5emLCons0.5em(a,0.5eml)0.5emwhen0.5emn0.5em>0.5em10.5em->0.5ema::(ltake0.5em(n-1)0.5em(Lazy.force0.5eml))0.5em0.5emLCons0.5em(a,0.5eml)0.5emwhen0.5emn0.5em=0.5em10.5em->0.5em[a]Avoid forcing the tail if not needed.0.5em->0.5em[]let0.5emrec0.5emlappend0.5eml10.5eml20.5em=0.5em0.5emmatch0.5eml10.5emwith0.5emLNil0.5em->0.5emLazy.force0.5eml20.5em0.5em0.5emLCons0.5em(hd,0.5emtl)0.5em-> LCons0.5em(hd,0.5emlazy0.5em(lappend0.5em(Lazy.force0.5emtl)0.5eml2))let0.5emrec0.5emlconcatmap0.5emf0.5em=0.5emfunction0.5em0.5em0.5emLNil0.5em->0.5emLNil0.5em0.5em0.5emLCons0.5em(a,0.5eml)0.5em->0.5emlappend0.5em(f0.5ema)0.5em(lazy0.5em(lconcatmap0.5emf0.5em(Lazy.force0.5eml)))module0.5emLListM0.5em=0.5emMonadPlus0.5em(struct0.5em0.5emtype0.5em’a0.5emt0.5em=0.5em’a0.5emllist0.5em0.5emlet0.5embind0.5ema0.5emb0.5em=0.5emlconcatmap0.5emb0.5ema0.5em0.5emlet0.5emreturn0.5ema0.5em=0.5emLCons0.5em(a,0.5emlazy0.5emLNil)0.5em0.5emlet0.5emmzero0.5em=0.5emLNil0.5em0.5emlet0.5emmplus0.5em=0.5emlappendend)Parser Combinators: the Parsec* Monad

   • File Parsec.ml:

   open0.5emMonadmodule0.5emtype0.5emPARSE0.5em=0.5emsig0.5em0.5emtype0.5em'a0.5embacktrackingmonadName for the underlying monad-plus.0.5em0.5emtype0.5em’a0.5emparsingstate0.5em=0.5emint0.5em->0.5em(‘a0.5em0.5emint)0.5embacktrackingmonadProcessing state – position.0.5em0.5emtype0.5em’a0.5emt0.5em=0.5emstring0.5em->0.5em'a0.5emparsingstateReader for the parsed text.0.5em0.5eminclude0.5emMONADPLUSOPS0.5em0.5emval0.5em(<>)0.5em:0.5em’a0.5emmonad0.5em->0.5em’a0.5emmonad0.5emLazy.t0.5em->0.5em'a0.5emmonadA synonym for mplus.0.5em0.5emval0.5emrun0.5em:0.5em’a0.5emmonad0.5em->0.5em’a0.5emt0.5em0.5emval0.5emrunT0.5em:0.5em’a0.5emmonad0.5em->0.5emstring0.5em->0.5emint0.5em->0.5em’a0.5embacktrackingmonad0.5em0.5emval0.5emsatisfy0.5em:0.5em(char0.5em->0.5embool)0.5em->0.5emchar0.5emmonadConsume a character of the specified class.0.5em0.5emval0.5emendoftext0.5em:0.5emunit0.5emmonadCheck for end of the processed text.endmodule0.5emParseT0.5em(MP0.5em:0.5emMONADPLUSOPS)0.5em:0.5em0.5emPARSE0.5emwith0.5emtype0.5em’a0.5embacktrackingmonad0.5em:=0.5em’a0.5emMP.monad0.5em=struct0.5em0.5emtype0.5em’a0.5embacktrackingmonad0.5em=0.5em’a0.5emMP.monad0.5em0.5emtype0.5em’a0.5emparsingstate0.5em=0.5emint0.5em->0.5em(’a0.5em0.5emint)0.5emMP.monad0.5em0.5emmodule0.5emM0.5em=0.5emstruct0.5em0.5em0.5em0.5emtype0.5em’a0.5emt0.5em=0.5emstring0.5em->0.5em’a0.5emparsingstate0.5em0.5em0.5em0.5em0.5emlet0.5emreturn0.5ema0.5em=0.5emfun0.5ems0.5emp0.5em->0.5emMP.return0.5em(a,0.5emp)0.5em0.5em0.5em0.5emlet0.5embind0.5emm0.5emb0.5em=0.5emfun0.5ems0.5emp0.5em->0.5em0.5em0.5em0.5em0.5em0.5emMP.bind0.5em(m0.5ems0.5emp)0.5em(fun0.5em(a,0.5emp’)0.5em->0.5emb0.5ema0.5ems0.5emp’)0.5em0.5em0.5em0.5emlet0.5emmzero0.5em=0.5emfun0.5em0.5em_0.5em->0.5emMP.mzero0.5em0.5em0.5em0.5emlet0.5emmplus0.5emma0.5emmb0.5em=0.5emfun0.5ems0.5emp0.5em->0.5em0.5em0.5em0.5em0.5em0.5emMP.mplus0.5em(ma0.5ems0.5emp)0.5em(lazy0.5em(Lazy.force0.5emmb0.5ems0.5emp))0.5em0.5emend0.5em0.5eminclude0.5emM0.5em0.5eminclude0.5emMonadPlusOps(M)0.5em0.5emlet0.5em(<>)0.5emma0.5emmb0.5em=0.5emmplus0.5emma0.5emmb0.5em0.5emlet0.5emrunT0.5emm0.5ems0.5emp0.5em=0.5emMP.lift0.5emfst0.5em(m0.5ems0.5emp)0.5em0.5emlet0.5emsatisfy0.5emf0.5ems0.5emp0.5em=0.5em0.5em0.5em0.5emif0.5emp0.5em<0.5emString.length0.5ems0.5em&&0.5emf0.5ems.[p]Consuming a character means accessing it0.5em0.5em0.5em0.5emthen0.5emMP.return0.5em(s.[p],0.5emp0.5em+0.5em1)0.5emelse0.5emMP.mzeroand advancing the parsing position.0.5em0.5emlet0.5emendoftext0.5ems0.5emp0.5em=0.5em0.5em0.5em0.5emif0.5emp0.5em>=0.5emString.length0.5ems0.5emthen0.5emMP.return0.5em((),0.5emp)0.5emelse0.5emMP.mzeroendmodule0.5emtype0.5emPARSEOPS0.5em=0.5emsig0.5em0.5eminclude0.5emPARSE0.5em0.5emval0.5emmany0.5em:0.5em’a0.5emmonad0.5em->0.5em’a0.5emlist0.5emmonad0.5em0.5emval0.5emopt0.5em:0.5em’a0.5emmonad0.5em->0.5em’a0.5emoption0.5emmonad0.5em0.5emval0.5em(?)0.5em:0.5em’a0.5emmonad0.5em->0.5em’a0.5emoption0.5emmonad0.5em0.5emval0.5emseq0.5em:0.5em’a0.5emmonad0.5em->0.5em’b0.5emmonad0.5emLazy.t0.5em->0.5em(‘a0.5em0.5em’b)0.5emmonadExercise: why laziness here?0.5em0.5emval0.5em(<>)0.5em:0.5em’a0.5emmonad0.5em->0.5em’b0.5emmonad0.5emLazy.t0.5em->0.5em(’a0.5em0.5em’b)0.5emmonadSynonym for seq.0.5em0.5emval0.5emlowercase0.5em:0.5emchar0.5emmonad0.5em0.5emval0.5emuppercase0.5em:0.5emchar0.5emmonad0.5em0.5emval0.5emdigit0.5em:0.5emchar0.5emmonad0.5em0.5emval0.5emalpha0.5em:0.5emchar0.5emmonad0.5em0.5emval0.5emalphanum0.5em:0.5emchar0.5emmonad0.5em0.5emval0.5emliteral0.5em:0.5emstring0.5em->0.5emunit0.5emmonadConsume characters of the given string.0.5em0.5emval0.5em(<<>)0.5em:0.5emstring0.5em->0.5em’a0.5emmonad0.5em->0.5em'a0.5emmonadPrefix and postfix keywords.0.5em0.5emval0.5em(<>>)0.5em:0.5em’a0.5emmonad0.5em->0.5emstring0.5em->0.5em’a0.5emmonadendmodule0.5emParseOps0.5em(R0.5em:0.5emMONADPLUSOPS)0.5em0.5em(P0.5em:0.5emPARSE0.5emwith0.5emtype0.5em’a0.5embacktrackingmonad0.5em:=0.5em’a0.5emR.monad)0.5em:0.5em0.5emPARSEOPS0.5emwith0.5emtype0.5em’a0.5embacktrackingmonad0.5em:=0.5em’a0.5emR.monad0.5em=struct0.5em0.5eminclude0.5emP0.5em0.5emlet0.5emrec0.5emmany0.5emp0.5em=0.5em0.5em0.5em0.5em(perform0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5emr0.5em<–0.5emp;0.5emrs0.5em<–0.5emmany0.5emp;0.5emreturn0.5em(r::rs))0.5em0.5em0.5em0.5em++0.5emlazy0.5em(return0.5em[])0.5em0.5emlet0.5emopt0.5emp0.5em=0.5em(p0.5em>>=0.5em(fun0.5emx0.5em->0.5emreturn0.5em(Some0.5emx)))0.5em++0.5emlazy0.5em(return0.5emNone)0.5em0.5emlet0.5em(?)0.5emp0.5em=0.5emopt0.5emp0.5em0.5emlet0.5emseq0.5emp0.5emq0.5em=0.5emperform0.5em0.5em0.5em0.5em0.5em0.5emx0.5em<–0.5emp;0.5emy0.5em<–0.5emLazy.force0.5emq;0.5emreturn0.5em(x,0.5emy)0.5em0.5emlet0.5em(<>)0.5emp0.5emq0.5em=0.5emseq0.5emp0.5emq0.5em0.5emlet0.5emlowercase0.5em=0.5emsatisfy0.5em(fun0.5emc0.5em->0.5emc0.5em>=0.5em’a’0.5em&&0.5emc0.5em<=0.5em’z’)0.5em0.5emlet0.5emuppercase0.5em=0.5emsatisfy0.5em(fun0.5emc0.5em->0.5emc0.5em>=0.5em’A’0.5em&&0.5emc0.5em<=0.5em’Z’)0.5em0.5emlet0.5emdigit0.5em=0.5emsatisfy0.5em(fun0.5emc0.5em->0.5emc0.5em>=0.5em’0’0.5em&&0.5emc0.5em<=0.5em’9’)0.5em0.5emlet0.5emalpha0.5em=0.5emlowercase0.5em++0.5emlazy0.5emuppercase0.5em0.5emlet0.5emalphanum0.5em=0.5emalpha0.5em++0.5emlazy0.5emdigit0.5em0.5emlet0.5emliteral0.5eml0.5em=0.5em0.5em0.5em0.5emlet0.5emrec0.5emloop0.5empos0.5em=0.5em0.5em0.5em0.5em0.5em0.5emif0.5empos0.5em=0.5emString.length0.5eml0.5emthen0.5emreturn0.5em()0.5em0.5em0.5em0.5em0.5em0.5emelse0.5emsatisfy0.5em(fun0.5emc0.5em->0.5emc0.5em=0.5eml.[pos])0.5em>>-0.5emloop0.5em(pos0.5em+0.5em1)0.5emin0.5em0.5em0.5em0.5emloop0.5em00.5em0.5emlet0.5em(<<>)0.5embra0.5emp0.5em=0.5emliteral0.5embra0.5em>>-0.5emp0.5em0.5emlet0.5em(<>>)0.5emp0.5emket0.5em=0.5emp0.5em>>=0.5em(fun0.5emx0.5em->0.5emliteral0.5emket0.5em>>-0.5emreturn0.5emx)endParser Combinators: Tying the Recursive Knot

   • File PluginBase.ml:

   module0.5emParseM0.5em=0.5em0.5emParsec.ParseOps0.5em(Monad.LListM)0.5em(Parsec.ParseT0.5em(Monad.LListM))open0.5emParseMlet0.5emgrammarrules0.5em:0.5em(int0.5emmonad0.5em->0.5emint0.5emmonad)0.5emlist0.5emref0.5em=0.5emref0.5em[]let0.5emgetlanguage0.5em()0.5em:0.5emint0.5emmonad0.5em=0.5em0.5emlet0.5emrec0.5emresult0.5em=0.5em0.5em0.5em0.5emlazy0.5em0.5em0.5em0.5em0.5em0.5em(List.foldleft0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em(fun0.5emacc0.5emlang0.5em->0.5emacc0.5em<>0.5emlazy0.5em(lang0.5em(Lazy.force0.5emresult)))0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5emmzero0.5em!grammarrules)0.5eminEnsure we parse the whole text.0.5em0.5emperform0.5emr0.5em<–0.5emLazy.force0.5emresult;0.5emendoftext;0.5emreturn0.5emrParser Combinators: Dynamic Code Loading

   • File PluginRun.ml:

   let0.5emloadplug0.5emfname0.5em:0.5emunit0.5em=0.5em0.5emlet0.5emfname0.5em=0.5emDynlink.adaptfilename0.5emfname0.5emin0.5em0.5emif0.5emSys.fileexists0.5emfname0.5emthen0.5em0.5em0.5em0.5emtry0.5emDynlink.loadfile0.5emfname0.5em0.5em0.5em0.5emwith0.5em0.5em0.5em0.5em0.5em0.5em(Dynlink.Error0.5emerr)0.5emas0.5eme0.5em->0.5em0.5em0.5em0.5em0.5em0.5emPrintf.printf0.5em”0.5emloading0.5emplugin:0.5em%s%!“0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em(Dynlink.errormessage0.5emerr);0.5em0.5em0.5em0.5em0.5em0.5emraise0.5eme0.5em0.5em0.5em0.5em0.5eme0.5em->0.5emPrintf.printf0.5em”0.5emerror0.5emwhile0.5emloading0.5emplugin%!“0.5em0.5emelse0.5em(0.5em0.5em0.5em0.5emPrintf.printf0.5em”0.5emfile0.5em%s0.5emdoes0.5emnot0.5emexist%!“0.5emfname;0.5em0.5em0.5em0.5emexit0.5em(-1))let0.5em()0.5em=0.5em0.5emfor0.5emi0.5em=0.5em20.5emto0.5emArray.length0.5emSys.argv0.5em-0.5em10.5emdo0.5em0.5em0.5em0.5emloadplug0.5emSys.argv.(i)0.5emdone;0.5em0.5emlet0.5emlang0.5em=0.5emPluginBase.getlanguage0.5em()0.5emin0.5em0.5emlet0.5emresult0.5em=0.5em0.5em0.5em0.5emMonad.LListM.run0.5em0.5em0.5em0.5em0.5em0.5em(PluginBase.ParseM.runT0.5emlang0.5emSys.argv.(1)0.5em0)0.5emin0.5em0.5emmatch0.5emMonad.ltake0.5em10.5emresult0.5emwith0.5em0.5em0.5em[]0.5em->0.5emPrintf.printf0.5em”0.5emerror%!“0.5em0.5em0.5emr::0.5em->0.5emPrintf.printf0.5em”:0.5em%d%!“0.5emrParser Combinators: Toy Example

   • File Plugin1.ml:

   open0.5emPluginBase.ParseMlet0.5emdigitofchar0.5emd0.5em=0.5emintofchar0.5emd0.5em-0.5emintofchar0.5em’0’let0.5emnumber=0.5em0.5emlet0.5emrec0.5emnum0.5em=Numbers: N := D N | D where D is digits.0.5em0.5em0.5em0.5emlazy0.5em(0.5em0.5em(perform0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5emd0.5em<–0.5emdigit;0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em(n,0.5emb)0.5em<–0.5emLazy.force0.5emnum;0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5em0.5emreturn0.5em(digitofchar0.5emd0.5em0.5emb0.5em+0.5emn,0.5emb0.5em0.5em10))0.5em0.5em0.5em0.5em0.5em0.5em<>0.5emlazy0.5em(digit0.5em>>=0.5em(fun0.5emd0.5em->0.5emreturn0.5em(digitofchar0.5emd,0.5em10))))0.5emin0.5em0.5emLazy.force0.5emnum0.5em>>0.5emfstlet0.5emaddition0.5emlang0.5em=Addition rule: S \rightarrow (S + S).0.5em0.5emperformRequiring a parenthesis ( turns the rule into non-left-recursive.0.5em0.5em0.5em0.5emliteral0.5em”(“;0.5emn10.5em<–0.5emlang;0.5emliteral0.5em”+“;0.5emn20.5em<–0.5emlang;0.5emliteral0.5em”)“;0.5em0.5em0.5em0.5emreturn0.5em(n10.5em+0.5emn2)let0.5em()0.5em= PluginBase.(grammarrules0.5em:=0.5emnumber0.5em::0.5emaddition0.5em::0.5em!grammarrules)

   • File Plugin2.ml:

   open0.5emPluginBase.ParseMlet0.5emmultiplication0.5emlang0.5em=0.5em0.5emperformMultiplication rule: S \rightarrow (S \ast S).0.5em0.5em0.5em0.5emliteral0.5em”(“;0.5emn10.5em<–0.5emlang;0.5emliteral0.5em”“;0.5emn20.5em<–0.5emlang;0.5emliteral0.5em”)“;0.5em0.5em0.5em0.5emreturn0.5em(n10.5em0.5emn2)let0.5em()0.5em= PluginBase.(grammarrules0.5em:=0.5emmultiplication0.5em::0.5em!grammarrules)

   Functional ProgrammingŁukasz Stafiniak

   The Expression Problem

   Exercise 1: Implement the string_of_ functions or methods, covering all data cases, corresponding to the eval_ functions in at least two examples from the lecture, including both an object-based example and a variant-based example (either standard, or polymorphic, or extensible variants).

   Exercise 2: Split at least one of the examples from the previous exercise into multiple files and demonstrate separate compilation.

   Exercise 3: Can we drop the tags Lambda_t, Expr_t and LExpr_t used in the examples based on standard variants (file FP_ADT.ml)? When using polymorphic variants, such tags are not needed.

   Exercise 4: Factor-out the sub-language consisting only of variables, thus eliminating the duplication of tags VarL, VarE in the examples based on standard variants (file FP_ADT.ml).

   Exercise 5: Come up with a scenario where the extensible variant types-based solution leads to a non-obvious or hard to locate bug.

   Exercise 6: * Re-implement the direct object-based solution to the expression problem (file Objects.ml) to make it more satisfying. For example, eliminate the need for some of the rename, apply, compute methods.

   Exercise 7: Re-implement the visitor pattern-based solution to the expression problem (file Visitor.ml) in a functional way, i.e. replace the mutable fields subst and beta_redex in the eval_lambda class with a different solution to the problem of treating abs and non-abs expressions differently.

   ** See if you can replace the reference cells result in evalN and freevarsN functions (for N=1,2,3) with a different solution to the problem of polymorphism wrt. the type of the computed values.*

   Exercise 8: Extend the sub-language expr_visit with variables, and add to arguments of the evaluation constructor eval_expr the substitution. Handle the problem of potentially duplicate fields subst. (One approach might be to use ideas from exercise 6.)

   Exercise 9: Impement the following modifications to the example from the file PolyV.ml:

   1. Factor-out the sub-language of variables, around the already present *var* type.
   2. Open the types of functions *eval3*,*freevars3* and other functions as required, so that explicit subtyping, e.g. in eval30.5em[]0.5em(test20.5em:>0.5emlexprt), is not necessary.
   3. Remove the double-dispatch currently in *eval_lexpr* and *freevars_lexpr*, by implementing a cascading design rather than a “divide-and-conquer” design.

   Exercise 10: Streamline the solution PolyRecM.ml by extending the language of \lambda-expressions with arithmetic expressions, rather than defining the sub-languages separately and then merging them. See slide on page 15 of Jacques Garrigue Structural Types, Recursive Modules, and the Expression Problem.

   Exercise 11: Transform a parser monad, or rewrite the parser monad transformer, by adding state for the line and column numbers.

   ** How to implement a monad transformer transformer in OCaml?*

   Exercise 12: Implement _of_string functions as parser combinators on top of the example PolyRecM.ml. Sections 4.3 and 6.2 of Monadic Parser Combinators by Graham Hutton and Erik Meijer might be helpful. Split the result into multiple files as in Exercise 2 and demonstrate dynamic loading of code.

   Exercise 13: What are the benefits and drawbacks of our lazy-monad-plus (built on top of odd lazy lists) approach, as compared to regular monad-plus built on top of even lazy lists? To additionally illustrate your answer:

   1. Rewrite the parser combinators example to use regular monad-plus and even lazy lists.
   2. Select one example from Lecture 8 and rewrite it using lazy-monad-plus and odd lazy lists.

   Exam: Exercises for review

   Exam set 0

   Exercise 1.

   Give types of the following expressions, either by guessing or inferring them by hand:

   1. let double f y = f (f y) in fun g x -> double (g x)
   2. let rec tails l = match l with [] -> [] | x::xs -> xs::tails xs infun l -> List.combine l (tails l)

   Exercise 2.

   Assume that the corresponding expression from previous exercise is bound to name foo. What are the values computed for the expressions (compute in your head or derive on paper):

   1. foo (+) 2 3, foo ( * ) 2 3, foo ( * ) 3 2
   2. foo [1; 2; 3]

   Exercise 3.

   Give example expressions that have the following types (without using type constraints):

   1. (int -> int) -> bool
   2. 'a option -> 'a list

   Exercise 4.

   Write function that returns the list of all lists containing elements from the input list, preserving order from the input list, but without two elements.

   Exercise 5.

   Write a breadth-first-search function that returns an element from a binary tree for which a predicate holds, or None if no such element exists. The function should have signature:

   val bfs : ('a -> bool) -> 'a btree -> 'a option

   Exercise 6.

   Solve the n-queens problem using backtracking based on lists.

   Available functions: from_to, concat_map, concat_foldl, unique.

   Hint functions (asking for hint each loses one point): valid_queens, add_queen, find_queen, find_queens. Final function solve takes n as an argument. Each function, other than valid_queens that takes 3 lines, fits on one line.

   Exercise 7.

   Provide an algebraic specification and an implementation for first-in-first-out queues (lecture 5 exercise 9).

   Exam set 1

   Functional ProgrammingFebruary 5th 2013

   Exam set 1

   Exercise 1: (Blue.) What is the type of the subexpression y as part of the expression below assuming that the whole expression has the type given?

   *(fun double g x -> double (g x)) (fun f y -> f (f

   y

   ))*

   : (’a -> ’b -> ’b) -> ’a -> ’b -> ’b

   Exercise 2: (Blue.) Write an example function with type:

   *((int -> int) -> bool) -> int*

   Tell “in your words” what it does.

   Exercise 3: (Green.) Write a function last : 'a list -> 'a option that returns the last element of a list.

   Exercise 4: (Green.) Duplicate the elements of a list.

   Exercise 5: (Yellow.) Drop every N’th element from a list.

   Exercise 6: (Yellow.) Construct completely balanced binary trees of given depth.

   In a completely balanced binary tree, the following property holds for every node: The number of nodes in its left subtree and the number of nodes in its right subtree are almost equal, which means their difference is not greater than one.

   Write a function cbal_tree to construct completely balanced binary trees for a given number of nodes. The function should generate the list of all solutions (e.g. via backtracking). Put the letter 'x' as information into all nodes of the tree.

   Exercise 7: (White.) Due to Yaron Minsky.

   Consider a datatype to store internet connection information. The time when_initiated marks the start of connecting and is not needed after the connection is established (it is only used to decide whether to give up trying to connect). The ping information is available for established connection but not straight away.

   type connectionstate = | Connecting | Connected | Disconnectedtype connectioninfo = { state : connectionstate; server : Inetaddr.t; lastpingtime : Time.t option; lastpingid : int option; sessionid : string option; wheninitiated : Time.t option; whendisconnected : Time.t option;}

   (The types Time.t and Inetaddr.t come from the library Core* used where Yaron Minsky works. You can replace them with float and Unix.inet_addr. Load the Unix library in the interactive toplevel by #load "unix.cma";;.) Rewrite the type definitions so that the datatype will contain only reasonable combinations of information.*

   Exercise 8: (White.) Design an algebraic specification and write a signature for first-in-first-out queues. Provide two implementations: one straightforward using a list, and another one using two lists: one for freshly added elements providing efficient queueing of new elements, and “reversed” one for efficient popping of old elements.

   Exercise 9: (Orange.) Implement while_do in terms of repeat_until.

   Exercise 10: (Orange.) Implement a map from keys to values (a dictionary) using only functions (without data structures like lists or trees).

   Exercise 11: (Purple.) One way to express constraints on a polymorphic function is to write its type in the form: \forall \alpha _{1} \ldots \alpha _{n} [C] . \tau, where \tau is the type of the function, \alpha _{1} \ldots \alpha _{n} are the polymorphic type variables, and C are additional constraints that the variables \alpha _{1} \ldots \alpha _{n} have to meet. Let’s say we allow “local variables” in C: for example C = \exists \beta . \alpha _{1} \dot{=} \operatorname{list} (\beta). Why the general form \forall \beta [C] . \beta is enough to express all types of the general form \forall \alpha _{1} \ldots \alpha _{n} [C] . \tau?

   Exercise 12: (Purple.) Define a type that corresponds to a set with a googleplex of elements (i.e. 10^{10^{100}} elements).

   Exercise 13: (Red.) In a height-balanced binary tree, the following property holds for every node: The height of its left subtree and the height of its right subtree are almost equal, which means their difference is not greater than one. Consider a height-balanced binary tree of height h. What is the maximum number of nodes it can contain? Clearly, \operatorname{maxN}= 2 h - 1. However, finding the minimum number \operatorname{minN} is more difficult.

   Construct all the height-balanced binary trees with a given nuber of nodes. hbal_tree_nodes n returns a list of all height-balanced binary tree with n nodes.

   Find out how many height-balanced trees exist for n = 15.

   Exercise 14: (Crimson.) To construct a Huffman code for symbols with probability/frequency, we can start by building a binary tree as follows. The algorithm uses a priority queue where the node with lowest probability is given highest priority:

   1. Create a leaf node for each symbol and add it to the priority queue.
   2. While there is more than one node in the queue:
      1. Remove the two nodes of highest priority (lowest probability) from the queue.
      2. Create a new internal node with these two nodes as children and with probability equal to the sum of the two nodes’ probabilities.
      3. Add the new node to the queue.
   3. The remaining node is the root node and the tree is complete.

   Label each left edge by 0 and right edge by 1. The final binary code assigns the string of bits on the path from root to the symbol as its code.

   We suppose a set of symbols with their frequencies, given as a list of Fr(S,F) terms. Example: fs = [Fr(a,45); Fr(b,13); Fr(c,12); Fr(d,16); Fr(e,9); Fr(f,5)]. Our objective is to construct a list Hc(S,C) terms, where C is the Huffman code word for the symbol S. In our example, the result could be hs = [Hc(a,'0'); Hc(b,'101'); Hc(c,'100'); Hc(d,'111'); Hc(e,'1101'); Hc(f,'1100')] [Hc(a,'01'),…etc.]. The task shall be performed by the function huffman defined as follows: huffman(fs) returns the Huffman code table for the frequency table fs.

   Exercise 15: (Black.) Implement the Gaussian Elimination algorithm for solving linear equations and inverting square invertible matrices.

   Exam set 2

   Functional ProgrammingFebruary 5th 2013

   Exam set 2

   Exercise 1: (Blue.) What is the type of the subexpression f as part of the expression below assuming that the whole expression has the type given?

   *(fun double g x -> double (g x)) (fun f y ->

   (f y))*

   : (’a -> ’b -> ’b) -> ’a -> ’b -> ’b

   Exercise 2: (Blue.) Write an example function with type:

   *(int -> int list) -> bool*

   Tell “in your words” what it does.

   Exercise 3: (Green.) Find the number of elements of a list.

   Exercise 4: (Green.) Split a list into two parts; the length of the first part is given.

   Exercise 5: (Yellow.) Rotate a list N places to the left.

   Exercise 6: (Yellow.) Let us call a binary tree symmetric if you can draw a vertical line through the root node and then the right subtree is the mirror image of the left subtree. Write a function is_symmetric to check whether a given binary tree is symmetric.

   Exercise 7: (White.) By “traverse a tree” we mean: write a function that takes a tree and returns a list of values in the nodes of the tree. Traverse a tree in breadth-first order – first values in more shallow nodes.

   Exercise 8: (White.) Generate all combinations of K distinct elements chosen from the N elements of a list.

   Exercise 9: (Orange.) Implement a topological sort of a graph: write a function that either returns a list of graph nodes in topological order or informs (via exception or option type) that the graph has a cycle.

   Exercise 10: (Orange.) Express fold_left in terms of fold_right. Hint: continuation passing style.

   Exercise 11: (Purple.) Show why for a monomorphic specification, if datastructures d_{1} and d_{2} have the same behavior under all operations, then they have the same representation d_{1} = d_{2} in all implementations.

   Exercise 12: (Purple.) append for lazy lists returns in constant time. Where has its linear-time complexity gone? Explain how you would account for this in a time complexity analysis.

   Exercise 13: (Red.) Write a function ms_tree graph to construct the minimal spanning tree of a given weighted graph. A weighted graph will be represented as follows:

   *type 'a weighted_graph = {nodes : 'a list; edges : ('a * 'a * int) list}*

   The labels identify the nodes 'a uniquely and there is at most one edge between a pair of nodes. A triple (a,b,w) inside edges corresponds to edge between a and b with weight w. The minimal spanning tree is a subset of edges that forms an undirected tree, covers all nodes of the graph, and has the minimal sum of weights.

   Exercise 14: (Crimson.) Von Koch’s conjecture. Given a tree with N nodes (and hence N-1 edges). Find a way to enumerate the nodes from 1 to N and, accordingly, the edges from 1 to N-1 in such a way, that for each edge K the difference of its node numbers equals to K. The conjecture is that this is always possible.

   For small trees the problem is easy to solve by hand. However, for larger trees, and 14 is already very large, it is extremely difficult to find a solution. And remember, we don’t know for sure whether there is always a solution!

   Write a function that calculates a numbering scheme for a given tree. What is the solution for the larger tree pictured above?

   Exercise 15: (Black.) Based on our search engine implementation, write a function that for a list of keywords returns three best “next keyword” suggestions (in some sense of “best”, e.g. occurring in most of documents containing the given words).

   Exam set 3

   Functional ProgrammingFebruary 5th 2013

   Exam set 3

   Exercise 1: (Blue.) What is the type of the subexpression f y as part of the expression below assuming that the whole expression has the type given?

   *(fun double g x -> double (g x)) (fun f y -> f (

   ))*

   : (’a -> ’b -> ’b) -> ’a -> ’b -> ’b

   Exercise 2: (Blue.) Write an example function with type:

   *(int -> int -> bool option) -> bool list*

   Tell “in your words” what it does.

   Exercise 3: (Green.) Find the k’th element of a list.

   Exercise 4: (Green.) Insert an element at a given position into a list.

   Exercise 5: (Yellow.) Group the elements of a set into disjoint subsets. Represent sets as lists, preserve the order of elements. The required sizes of subsets are given as a list of numbers.

   Exercise 6: (Yellow.) A complete binary tree with height H is defined as follows: The levels 1, 2, 3, \ldots, H - 1 contain the maximum number of nodes (i.e 2^{i - 1} at the level i, note that we start counting the levels from 1 at the root). In level H, which may contain less than the maximum possible number of nodes, all the nodes are “left-adjusted”. This means that in a levelorder tree traversal all internal nodes come first, the leaves come second, and empty successors (the nil’s which are not really nodes!) come last.

   We can assign an address number to each node in a complete binary tree by enumerating the nodes in levelorder, starting at the root with number 1. In doing so, we realize that for every node X with address A the following property holds: The address of X’s left and right successors are 2A and 2A+1, respectively, supposed the successors do exist. This fact can be used to elegantly construct a complete binary tree structure. Write a function is_complete_binary_tree with the following specification: is_complete_binary_tree n t returns true iff t is a complete binary tree with n nodes.

   Exercise 7: (White.) Write two sorting algorithms, working on lists: merge sort and quicksort.

   1. Merge sort splits the list roughly in half, sorts the parts, and merges the sorted parts into the sorted result.
   2. Quicksort splits the list into elements smaller/greater than the first element, sorts the parts, and puts them together.

   Exercise 8: (White.) Express in terms of fold_left or fold_right, i.e.  with all recursion contained in the call to one of these functions, run-length encoding of a list (exercise 10 from 99 Problems).

   • *encode [‘a;‘a;‘a;‘a;‘b;‘c;‘c;‘a;‘a;‘d] = [4,‘a; 1,‘b; 2,‘c; 2,‘a; 1,‘d]*

   Exercise 9: (Orange.) Implement Priority Queue module that is an abstract data type for polymorphic queues parameterized by comparison function: the empty queue creation has signature

   val make_empty : leq:('a -> 'a -> bool) -> 'a prio_queue

   Provide only functions: make_empty, add, min, delete_min. Is this data structure “safe”?

   Implement the heap as a heap-ordered tree, i.e. in which the element at each node is no larger than the elements at its children. Unbalanced binary trees are OK.

   Exercise 10: (Orange.) Write a function that transposes a rectangular matrix represented as a list of lists.

   Exercise 11: (Purple.) Find the bijective functions between the types corresponding to a (a^b + c) and a^{b + 1} + ac (in OCaml).

   Exercise 12: (Purple.) Show the monad-plus laws for OptionM monad.

   Exercise 13: (Red.) As a preparation for drawing the tree, a layout algorithm is required to determine the position of each node in a rectangular grid. Several layout methods are conceivable, one of them is shown in the illustration below.

   

   In this layout strategy, the position of a node v is obtained by the following two rules:

   • x(v) is equal to the position of the node v in the inorder sequence;
   • y(v) is equal to the depth of the node v in the tree.

   In order to store the position of the nodes, we redefine the OCaml type representing a node (and its successors) as follows:

   type 'a pos_binary_tree =
       | E (* represents the empty tree *)
       | N of 'a * int * int * 'a pos_binary_tree * 'a pos_binary_tree

   N(w,x,y,l,r) represents a (non-empty) binary tree with root w “positioned” at (x,y), and subtrees l and r. Write a function layout_binary_tree with the following specification: layout_binary_tree t returns the “positioned” binary tree obtained from the binary tree t.

   An alternative layout method is depicted in the illustration:

   

   Find out the rules and write the corresponding function.

   Hint: On a given level, the horizontal distance between neighboring nodes is constant.

   Exercise 14: (Crimson.) Nonograms. Each row and column of a rectangular bitmap is annotated with the respective lengths of its distinct strings of occupied cells. The person who solves the puzzle must complete the bitmap given only these lengths.

             Problem statement:          Solution:
   
             |_|_|_|_|_|_|_|_| 3         |_|X|X|X|_|_|_|_| 3
             |_|_|_|_|_|_|_|_| 2 1       |X|X|_|X|_|_|_|_| 2 1
             |_|_|_|_|_|_|_|_| 3 2       |_|X|X|X|_|_|X|X| 3 2
             |_|_|_|_|_|_|_|_| 2 2       |_|_|X|X|_|_|X|X| 2 2
             |_|_|_|_|_|_|_|_| 6         |_|_|X|X|X|X|X|X| 6
             |_|_|_|_|_|_|_|_| 1 5       |X|_|X|X|X|X|X|_| 1 5
             |_|_|_|_|_|_|_|_| 6         |X|X|X|X|X|X|_|_| 6
             |_|_|_|_|_|_|_|_| 1         |_|_|_|_|X|_|_|_| 1
             |_|_|_|_|_|_|_|_| 2         |_|_|_|X|X|_|_|_| 2
              1 3 1 7 5 3 4 3             1 3 1 7 5 3 4 3
              2 1 5 1                     2 1 5 1

   For the example above, the problem can be stated as the two lists [[3];[2;1];[3;2];[2;2];[6];[1;5];[6];[1];[2]] and [[1;2];[3;1];[1;5];[7;1];[5];[3];[4];[3]] which give the “solid” lengths of the rows and columns, top-to-bottom and left-to-right, respectively. Published puzzles are larger than this example, e.g. 2520, and apparently always have unique solutions.*

   Exercise 15: (Black.) Leftist heaps are heap-ordered binary trees that satisfy the leftist property: the rank of any left child is at least as large as the rank of its right sibling. The rank of a node is defined to be the length of its right spine, i.e. the rightmost path from the node in question to an empty node. Implement O (\log n) worst case time complexity Priority Queues based on leftist heaps. Each node of the tree should contain its rank.

   Note that the elements along any path through a heap-ordered tree are stored in sorted order. The key insight behind leftist heaps is that two heaps can be merged by merging their right spines as you would merge two sorted lists, and then swapping the children of nodes along this path as necessary to restore the leftist property.